Абсолютное ускорение

а_а=(a_О1А²+a_┴О1А²)^0,5=20 м/с² и направлено от т. А к т. О. Тот же ответ получим, если определим а_а как нормальное ускорение т. А при ее вращательном движении вокруг т. О:

a_Аⁿ=ω²OA.

14 Вопрос

Теорема об изменении кинетической энергии точки.

Рассмотрим точку с массой т, перемещающуюся под действием при­ложенных к ней сил из положения M₀ , где она имеет скорость , в положение М₁ , где ее скорость равна .

Для получения искомой зависимости обратимся к уравнению выражающему основной закон динамики. Проектируя обе части этого равенства на касательную к траектории точ­ки М, направленную в сторону движения, получим:

Стоящую слева величину касательного ускорения можно пред­ставить в виде

.

В результате будем иметь:

.

Умножив обе части этого равенства на ds, внесем т под знак дифференциала. Тогда, замечая, что где - эле­ментарная работа силы F_k получим выражение теоремы об изме­нении кинетической энергии в дифференциальной форме:

.

Проинтегрировав теперь обе части этого равенства в пределах, соответствующих значениям переменных в точках M₀ и M₁, найдем окончательно:

.

Уравнение выражает теорему об изменении кине­тической энергии точки в конечном виде: изменение кинетической энергии точки при некотором ее перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении.

15 Вопрос

Работа силы - мера действия силы, зависящая от численной величины и направления силы F и от перемещения s точки её приложения. Если сила F численно и по направлению постоянная, а перемещение прямолинейно, то работа А = F·s cosα, где α — угол между направлениями силы и перемещения.

Мощность - физическая. величина N, измеряемая отношением работы A к промежутку времени t, в течение которого она совершена; если работа совершается равномерно, то N = A/t. Измеряется в ваттах.

17 Вопрос

Определение скорости и ускорения точки при координатном способе задания движения

Связь векторного способа задания движения и координатного дается соотношением

Из определения скорости

Проекции скорости на оси координат равны производным соответствующих координат по времени:

Модуль и направление скорости определяются выражениями

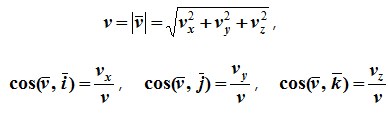
Из определения ускорения

Проекции ускорения на оси координат равны вторым производным соответствующих координат по времени

Модуль и направление ускорения определяются выражениями

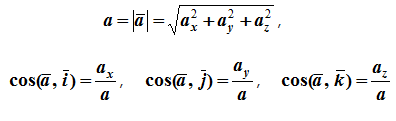
Равномерное криволинейное движение (v=const)

s=s₀+vt,

где s − дуговая координата; s₀ − дуговая координата в начальный момент времени при t=0.

,  , 

Вопрос 16

Теорема об изменении количества движения.     Количество движения материальной точки – векторная величина, которая равняется произведению массы точки на вектор ее скорости.     Единицей измерения количества движения есть (кг м/с) К. л. mv — величина векторная, направленная так же, как скорость точки. Иногда К. д. называют ещё импульсом

Согласно теореме об изменении К. д. Q₁—Q₀ = åS_k^e. где Q₀ и Q₁ — К. д. системы в начале и в конце некоторого промежутка времени, S_k^e — импульсы внешних сил F_k^e (см. Импульс силы) за этот промежуток времени (в дифференциальной форме теорема выражается уравнением   =åF_k^e).

Импульс силы характеризует действие силы за некоторый промежуток времени.    Импульс   силы   за конечный промежуток времени   определяется как интегральная сумма соответствующих элементарных импульсов      Теорема об изменении количества движения материальной точки: (в дифференциальной форме): Производная за временем от количества движения материальной точки равняется геометрической сумме действующих на точки сил (в интегральной форме): Изменение количества движения материальной точки за некоторый промежуток времени равняется геометрической сумме импульсов сил, приложенных к точке за тот же промежуток времени.

      Законы сохранения свидетельствуют, что внутренние силы не могут изменить суммарное количество движения системы.