8 Вопрос

Это - основополагающий физический процесс при движении вагонов, локомотивов и поездов по железным дорогам. Именно он во многом определяет такие важнейшие показатели, как нагрузка на ось, статическая нагрузка вагонов, масса и скорость движения составов

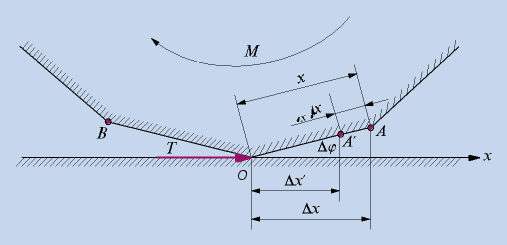
Качение колесной пары по рельсу под воздействием крутящего момента М сопровождается рассогласованием фактической линейной скорости колесного центра V и этой же скорости, вычисленной по угловой скорости колесной пары относительно собственной оси вращения (окружной скорости). Это рассогласование обычно оценивается величиной, называемой относительной скоростью продольного псевдоскольжения, v = (wr-V)/V (1)

где w — угловая скорость вращения колеса; r — радиус колеса; V — скорость движения колесного центра.

9 Вопрос

Скорость любой точки фигуры при ее плоском движении можно найти с помощью мгновенного центра скоростей (точки сечения, скорость которой в данный момент времени равна нулю). Положение мгновенного центра скоростей определяется как точка пересечения перпендикуляров к векторам скоростей двух точек тела. Угловую скорость тела ω можно найти из соотношения.

здесь т. Р − мгновенный центр скоростей, АР и ВР − расстояния от точек до мгновенного центра скоростей.

После того как положение мгновенного центра скоростей (т. Р) найдена, скорость любой точки тела определяется как вращательная скорость вокруг т. Р:

Теорема о движении центра масс

центр масс системы материальных точек движется как материальная точка, масса которой равна суммарной массе всей системы, а действующая сила – геометрической сумме всех внешних сил, действующих на все точки системы.

11 Вопрос

Для описания плоского  движения  тел достаточно описать движение точек  одного сечения тела плоскостью,  параллельной  неподвижной плоскости.

           Пусть тело перемещается параллельно неподвижной плоскости  П₁.    Проведем  через тело  параллельно ей плоскость  П₂ .   Сечение  тела по определению будет перемещаться в этой плоскости.

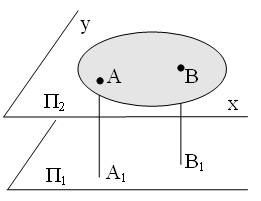         Возьмем две произвольные точки  ( А и В ) в сечении   и рассмотрим движение отрезков,  проведенных из точек перпендикулярно плоскости П₁.

        При движении тела отрезки АА₁ и ВВ₁ будут перемещаться параллельно самим себе, то есть  поступательно.    Это значит, что все точки отрезка АА₁ будут иметь одинаковые траектории, одинаковые скорости и одинаковые  ускорения.

       То же самое  можно сказать о скоростях и ускорениях  всех точек тела, расположенных на отрезке  ВВ₁.    Отсюда вывод о достаточности описания движения только точек тела, находящихся в сечении тела плоскостью,  параллельной неподвижной плоскости.

 Скорость  любой  точки  тела  при  плоском  движении  равна геометрической  сумме  скорости  полюса  и  скорости  во  вращении   точки  относительно  полюса.

             Ускорение   любой  точки  тела  при  плоском  движении  равно геометрической  сумме  ускорения  полюса и  ускорения  во  вращении точки  относительно  полюса.

          Первая теорема доказана. 

 Для  доказательства теоремы об ускорениях точек  продифференцируем  по  времени  теорему  о  сложении  скоростей.

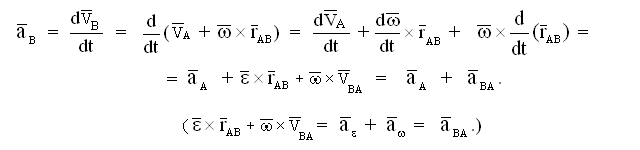
          Так как геометрическая сумма вращательного и осестремительного ускорений определяет полное ускорение т. В   в  ее вращении относительно полюса,  можно считать доказанной  и  вторую теорему.  Остается теперь внимательно разобраться с каждым из полученных векторных равенств и подумать об эффективном  применении этих равенств и следствий из них при решении задач.

  Из  теоремы   можно  получить несколько  очень полезных  для решения задач следствий.