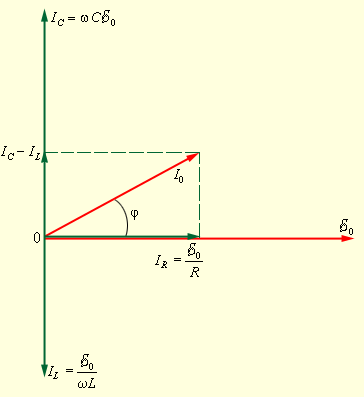
42,54. Закон Ома для электрических цепей переменного тока. Lсr – колебательный контур. Построение векторных диаграмм.

Соотношения, связывающие амплитуды переменных токов и напряжений на резисторе, конденсаторе и катушке индуктивности имеют вид:  (1)

Соотношение (1) выражают закон Ома для участка цепи переменного тока, содержащего один из элементов R, L и C. Физические величины R,  1/ωС и ωL называются активным сопротивлением резистора, емкостным сопротивлением конденсатора и индуктивным сопротивлением катушки. При протекании переменного тока по участку цепи электромагнитное поле совершает работу, и в цепи выделяется джоулево тепло. Мощность в цепи переменного тока выделяется только на активном сопротивлении. Средняя мощность переменного тока на конденсаторе и катушке индуктивности равна нулю. Рассмотрим теперь электрическую цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки. Цепь подключена к источнику переменного тока частоты ω. На всех последовательно соединенных участках цепи протекает один и тот же ток. Между напряжением внешнего источника e (t) и током J (t) возникает фазовый сдвиг на некоторый угол φ. Поэтому можно записать J (t) = I₀ cos ωt;   e (t) =  ₀ cos (ωt + φ). Такая запись мгновенных значений тока и напряжения соответствует построениям на векторной диаграмме. Как видно из векторной диаграммы, U_R =  ₀ · cos φ. Соотношение между амплитудами тока I₀ и напряжения  ₀ для последовательной RLC-цепи:  . Величину называют полным сопротивлением цепи переменного тока. Формулу, выражающую связь между амплитудными значениями тока и напряжения в цепи, можно записать в виде  ZI₀ =  ₀ (2). Это соотношение называют законом Ома для цепи переменного тока. Формулы (1), приведенные в начале этого параграфа, выражают частные случаи закона Ома (2). Для определения полного сопротивления цепи во многих случаях удобно использовать наглядный метод векторных диаграмм. Рассмотрим в качестве примера параллельный RLC-контур, подключенный к внешнему источнику переменного тока. При построении векторной диаграммы следует учесть, что при параллельном соединении напряжение на всех элементах R, C и L одно и то же и равно напряжению внешнего источника. Токи, текущие в разных ветвях цепи, отличаются не только по значениям амплитуд, но и по фазовым сдвигам относительно приложенного напряжения. Поэтому полное сопротивление цепи нельзя вычислить по законам параллельного соединения цепей постоянного тока. Из диаграммы следует:  . Поэтому полное сопротивление параллельного RLC-контура выражается соотношением 

44. Чему равно отношение значений магнитной индукции внутри бесконечно длинного соленоида и на срезе полубесконечного соленоида?

Б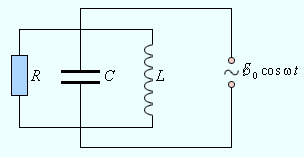 есконечно длинный соленоид симметричен любой, перпендикулярной к его оси плоскости. Взятые попарно, симметричные относительно такой плоскости витки создают поле, в котором вектор    перпендикулярен плоскости витка, т.е. линии магнитной индукции имеют направление параллельное оси соленоида внутри и вне его.       Из параллельности вектора    оси соленоида вытекает, что поле как внутри, так и вне соленоида должно быть однородным.       Возьмём воображаемый прямоугольный контур 1–2–3–4–1 и разместим его в соленоиде. . Второй и четвёртый интегралы равны нулю, т.к. вектор    перпендикулярен направлению обхода, т.е   .       Возьмём участок 3–4 – на большом расстоянии от соленоида, где поле стремится к нулю; и пренебрежём третьим интегралом, тогда , где    – магнитная индукция на участке  1–2 – внутри  соленоида,     – магнитная проницаемость вещества. Если отрезок 1–2 внутри соленоида, контур охватывает ток: где n – число витков на единицу длины, I – ток в соленоиде (в проводнике). Тогда магнитная индукция внутри соленоида: Вне соленоида: и   т.е.  Бесконечно длинный соленоид аналогичен плоскому конденсатору – и тут, и там поле однородно и сосредоточено внутри. У конца полубеск. соленоида, на его оси магнитная индукция равна: Тогда их отношение равно ½.