37,52.Сформулируйте закон Био-Савара-Лапласа. Пользуясь этим законом дайте вывод формулы для индукции магнитного поля на оси кругового витка с током

Закон Био Савара Лапласа определяет величину модуля вектора магнитной индукции в точке выбранной произвольно находящейся в магнитном поле. Поле при этом создано постоянным током на некотором участке. Формулировка закона Био Савара Лапласа имеет вид: При прохождении постоянного тока по замкнутому контуру, находящемуся в вакууме, для точки, отстоящей на расстоянии r0, от контура магнитная индукция будет иметь вид. . В этом случае α = π/2, sinα = 1; , где а – расстояние, отсчитываемое от центра витка до рассматриваемой точки на оси витка. Векторы образуют в этой точке конус с углом раствора при вершине 2 = π - 2β, где β – угол между отрезками а и r. Из соображений симметрии ясно, что результирующее магнитное поле на оси витка будет направлено вдоль этой оси, то есть вклад в него дают только те составляющие, которые параллельны оси витка: Результирующую величину индукции магнитного поля B на оси витка получим, проинтегрировав это выражение по длине контура от 0 до 2πR: или, подставив значение r:

38,48. Рассмотреть движение электрона в однородном магнитном поле в двух случаях: а) скорость электрона перпенд. вектору магнитной индукции; б) скорость электрона направлена под углом α к полю магнитной индукции?

Р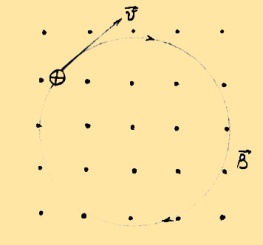 ассмотрим частный случай, когда нет электрического поля, но имеется магнитное поле. Предположим, что частица, обладающая начальной скоростью V₀, попадает в магнитное поле с индукцией B. Это поле мы будем считать однородным и направленным перпендикулярно к скорости V₀. Действующая на частицу сила Лоренца всегда перпендикулярна к скорости движения частицы. Это значит, что работа силы Лоренца всегда равна нулю; следовательно, абсолютное значение скорости движения частицы, а значит, и энергия частицы остаются постоянными при движении. Так как скорость частицы V не изменяется, то величина силы Лоренца остается постоянной. Эта сила, будучи перпендикулярной, к направлению движения, является центростремительной силой. Но движение под действием постоянной по величине центростремительной силы есть движение по окружности. Радиус r этой окружности определяется условием , откуда . Если энергия электрона выражена в эВ и равна U, то  и поэтому . Кругообразное движение заряженных частиц в магнитном поле обладает важной особенностью: время полного обращения частицы по окружности (период движения) не зависит от энергии частицы. Действительно, период обращения равен Подставляя сюда вместо r его выражение, имеем: , а частота равна . Для данного типа частиц и период, и частота зависят только от и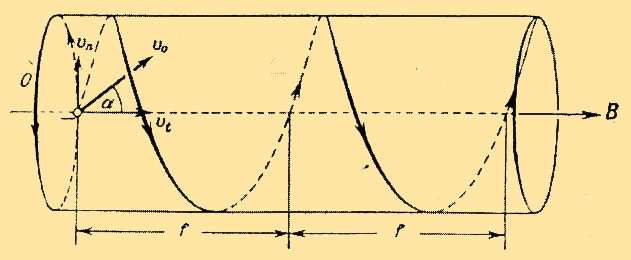 ндукции магнитного поля. Рассмотрим какой характер будет иметь движение, если начальная скорость частицы составляет некоторый угол с направлением поля. В этом случае удобно разложить скорость на две составляющие, одна из которых параллельна полю, а другая перпендикулярна к полю. На частицу действует сила Лоренца, и частица движется по окружности, лежащей в плоскости, перпендикулярной к полю. Составляющая Vt, не вызывает появления добавочной силы, так как сила Лоренца при движении параллельно полю равна нулю. Поэтому в направлении поля частица движется по инерции равномерно, со скоростью . В результате сложения обоих движений частица будет двигаться по цилиндрической спирали. Шаг винта этой спирали равен подставляя вместо T его выражение, имеем: