10.Сұрақ.Жоғарғы және төменгі шектердің тізбек жинақтылығымен байланысы.

Теорема1. Тізбектің шегі бар немесе плюс шексіздікке немесе минус шексіздікке ұмтылады, сонда және тек сонда ғана, егер оның төменгі және жоғарғы шектері тең болса.

Дәлелдеуі. Дәлелдеуін тек = = a R жағдайы үшін ғана келтіреміз. Онда = = , ал = = a болғандықтан , шек қасиеті бойынша =a .

Теорема2. Тізбек жинақты , сонда және тек сонда ғана , егер оның кез келген ішкі тізбегі жинақты болса.

Дәлелдеуі. Кез келген ішкі тізбектің төменгі және жоғарғы шектері қарастырылып отырған тізбектің төменгі және жоғарғы шектерінің арасында жатады. Егер тізбек жинақты болса , онда оның төменгі және жоғарғы шектері тең. Демек, сонда ішкі тізбектің де төменгі және жоғарғы шектері тең, мұнан оның жинақтылығы әрі берілген тізбек шегіне жинақталатыны шығады.

Кері тізбекті дәлелдеу үшін, ішкі тізбек үшін берілген тізбектің өзін алса болғаны.

11.Фундаментальдік тізбек. Коши критерийі. Берілген сандық { } тізбегі фундаментальдік немесе Коши тізбегі деп аталады , егер кез келген саны үшін N нөмірі табылып , барлық n>N, m>N үшін | | < теңсіздігі орындалса.

Мұның кванторлар арқылы жазылуын келтірейік:

{ } - фундаментальді := .

Теорема. Егер { } тізбегі фундаментальдік болса , онда

12) Бірінші тамаша шек =1

Мұны « » тіліндегі Коши анықтамасы көмегімен дәләлдейміз. Ең алдымен, егер 0 |x|<

болса , онда cosx < <1 (1)

теңсіздіктерінің орындалатынын дәлелдейік. Мұндағы cosx , функциялары жұп болғандықтан, 0 x< жағдайын ғана қарастыру жеткілікті. Суретте көрсетілген бір бұрышы х радианға тең болатын ОВА үшбұрышы, ОВА секторы және ОСА тікбұрышты үшбұрышының аудандары

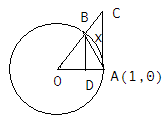
Қатынасында болатындығы айқын. Бұл теңсіздіктерден , ал одан (1) дәлелдеуі шығады. Енді (1) теңсіздіктерді (-1)-ге көбейтсек , -1 , ал оған 1-ді қосып, 0 теңсіздіктерін алып, оның оң жағының

= 2sin²

Екенін байқап , әрбір 0 |x|< үшін 1- |х|< <1 (2)

Теңсіздіктерінің орындалатынын көреміз.

Кез келген 0 санына сәйкес деп алсақ, онда 0 |x|< болғанда (2) бойынша 1 <1 ал бұл =1 деген сөз.

13) Екінші тамаша шек.

е (1)

Мұны тізбектер тіліндегі Гейне анықтамасы көмегімен дәлелдейік. Біз тізбектер теориясында = e

Деп е санын енгіздік. Онда оң бүтін сандардан құрылған кез келген өспелі {n_k} тізбегі үшін де

= e (2)

Шынында да, = e болғандықтан, кез келген саны үшін N саны табылып, барлық n>N үшін

,

Ал n_к ұмтылатын болғандықтан, барлық k>N үшін n_к > N. Сондықтан, k>N

болғанда .

Демек, (2) орындалады.