
- •2. Определенный интеграл
- •2.1. Понятие определенного интеграла
- •2.2. Геометрический смысл определенного интеграла
- •2.3. Основные свойства определенного интеграла
- •2.4. Оценки интегралов. Формула среднего значения
- •2.5. Связь между определенным и неопределенным интегралом. Интеграл с переменным верхним пределом
- •2.6. Формула Ньютона-Лейбница
- •2.7. Замена переменной в определенном интеграле
- •2.8. Интегрирование по частям в определенном интеграле
- •2.9. Несобственные интегралы
- •2.10. Некоторые геометрические приложения определенного интеграла
- •I. Вычисление площади плоской фигуры
- •II. Вычисление длины дуги плоской кривой
- •III. Вычисление объема тела
- •1) Вычисление объема тела по известным площадям поперечных сечений
- •2) Вычисление объема тела вращения
- •IV. Вычисление площади поверхности вращения
- •2.11. Приближенное вычисление определенных интегралов
- •2.12 Аудиторные задания и задания на повышение рейтинга
- •I. Вычислить определенные интегралы:
- •II. Вычислить площадь, ограниченную линиями:
- •III. Определить длину дуги кривой:
- •IV. Определить объем тела, образованного вращением фигуры, ограниченной линиями:
- •V. Определить площадь поверхности, образованной вращением кривой:
- •VI. Вычислить приближенно по формулам трапеций и Симпсона интегралы:
- •Задания
- •Решение типового варианта
- •Приложения Образец текущего контроля по модулю 4
- •Теоретические вопросы Интегральное исчисление функции одной переменной
- •Рекомендуемая литература Основная литература
- •Дополнительная литература
- •Методические пособия и указания, используемые в учебном процессе
Решение типового варианта
Пример 1. Найти неопределенные интегралы, результат проверить дифференцированием.
а)
![]() .
б)
.
б)
![]() .
.
в)
![]() .
г)
.
г)
![]() .
.
Решение.
а)
![]()
![]()

![]()
![]() .
.
б)
![]()
![]() .
.
в)
![]() .
.
г)
![]()
![]() .
.
Проверка.
а)
![]()
![]() .
.
б)
![]() .
.
в)
 .
.
г)
![]() .
.
![]() .
.
Пример 2. Найти неопределенные интегралы:
а)
![]() .
.
б)
![]()
Решение.
а)
![]() .
.
б)
![]()
![]()
Интеграл такого вида можно найти, применяя подходящую подстановку:
Решение (методом подстановки).
![]()
![]() .
.
Пример 3. Проинтегрировать по частям:
а)
![]() .
.
б)
![]() .
.
Решение.
а)

![]()
![]()
![]()
![]()
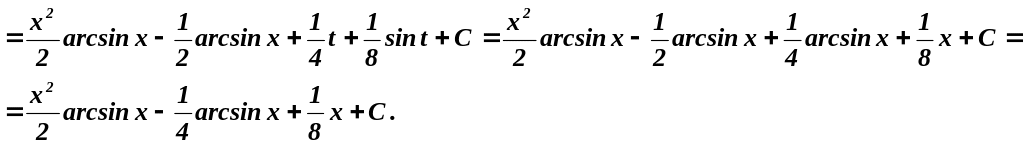 .
.
б)
![]()
![]() .
.
Пример 4. Найти интеграл от дробно-рациональной функции:
а)
![]() .
.
Решение.
а)
![]()
![]()
![]() .
.
Пример 5 . Найти интеграл от тригонометрической функции:
Решение.
![]()
![]()
![]()
![]() .
.
Пример
6.
Вычислить определенный интеграл
![]() с
точностью до двух знаков после запятой.
с
точностью до двух знаков после запятой.
Решение.
![]() .
.
Пример
7.
Найти площадь фигуры, ограниченной
заданными линиями:
![]() ,
,
![]() ,
.
,
.
Решение. Построим заданные кривые (см. рис. 19).
Н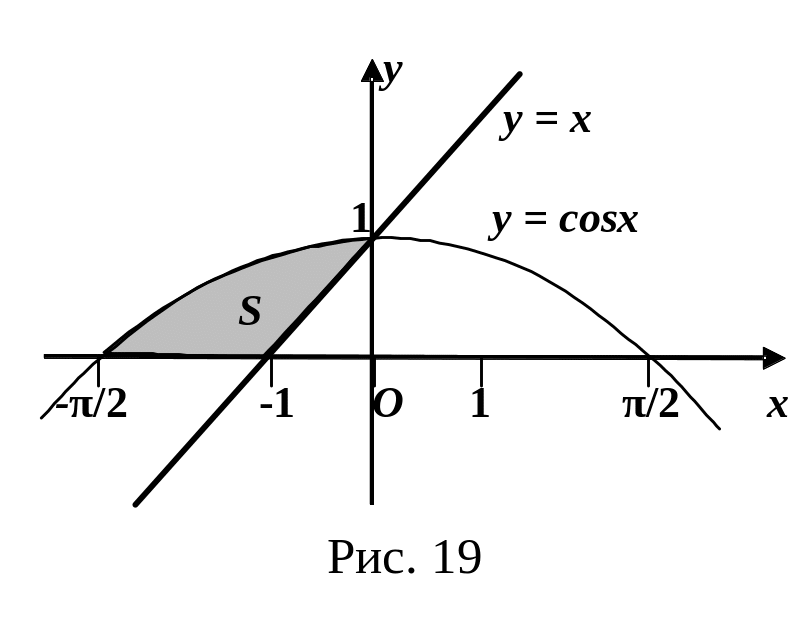 айдем
точки пересечения линий:
и
.
айдем
точки пересечения линий:
и
.
![]()
![]() .
Найдем точки пересечения линий:
и
.
.
Найдем точки пересечения линий:
и
.
![]()
![]() .
.
Найдем точки пересечения линий: и .
![]()
![]() .
Для
рассматриваемой фигуры
.
Для
рассматриваемой фигуры
![]() .
.
![]()
![]() .
.
Приложения Образец текущего контроля по модулю 4
Контрольная работа "Неопределенный интеграл”
М-4, КР
М – Модуль
КР – Контрольная работа
Вычислить неопределенные интегралы

Тестовое задание к модулю 4
"Интегральное исчисление функции одной переменной”
М-4, ТЗ - 4
М – Модуль
ТЗ – Тестовое задание
Функция F(x) является первообразной для функции f(x) в некотором промежутке, если в любой точке этого промежутка выполняется:
Функция F(x) является первообразной для функции f(x) в некотором промежутке, если в любой точке этого промежутка выполняется:
Если
 ,
то выполняется:
,
то выполняется:Неопределенный интеграл от дифференциала функции F(x) равен:
F(x)
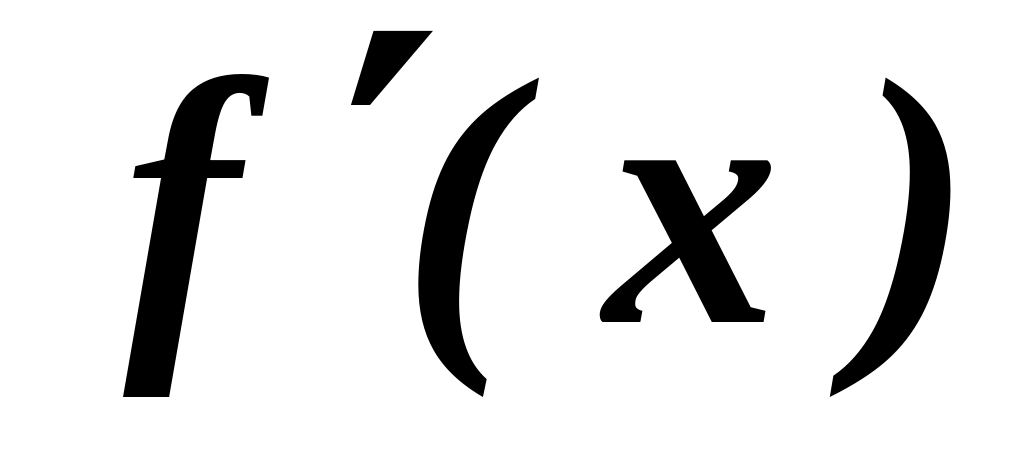
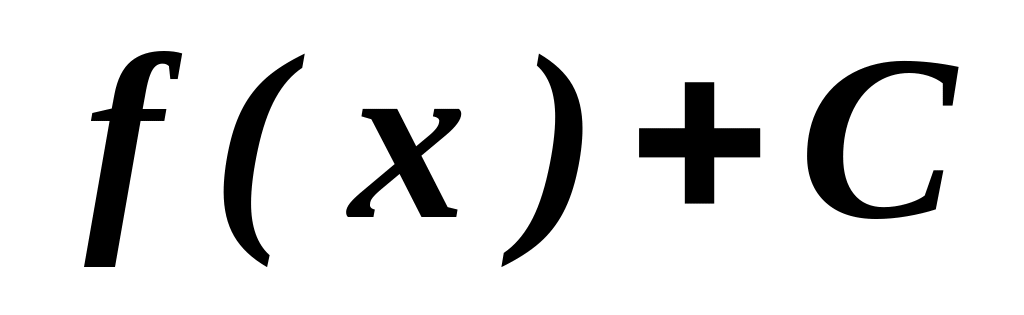

f(x)
Если функции F(x) – первообразная к функции f(x) на [a, b], то значение определенного интеграла
 равно:
равно:F(a)-F(b)
F(b)-F(a)

F(x)
Интеграл
 равен:
равен:Интеграл
 равен:
равен:Интеграл
 равен:
равен:Интеграл
 равен:
равен:Интеграл
 равен:
равен:Интеграл
 равен:
равен:Интеграл
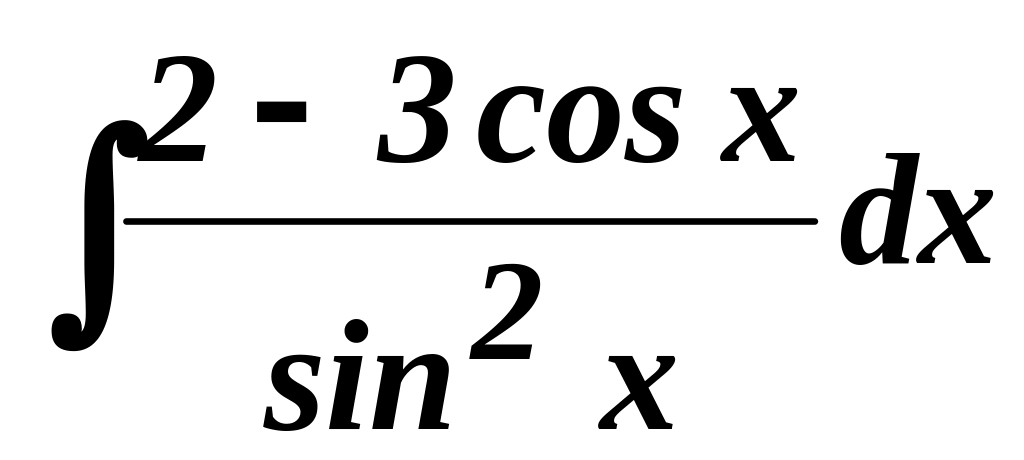 равен:
равен:Интеграл
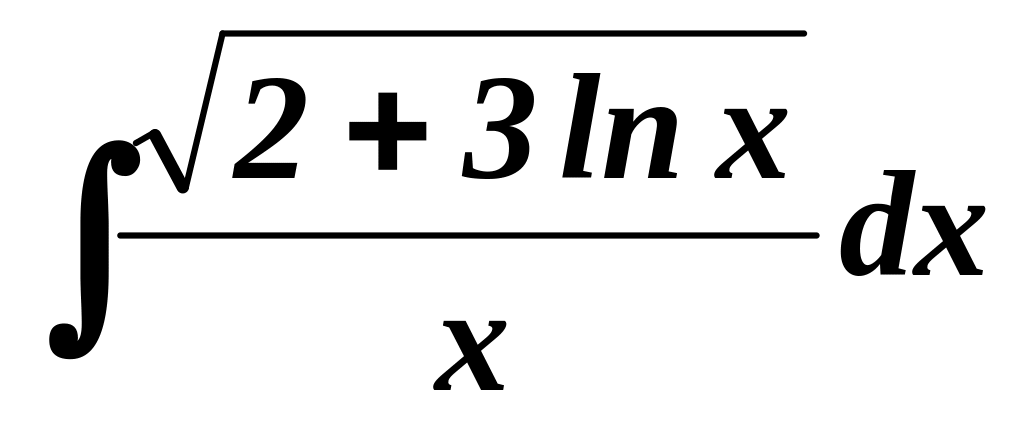 равен:
равен:Интеграл
 равен:
равен:Интеграл
 равен:
равен:Интеграл
 равен:
равен:Интеграл
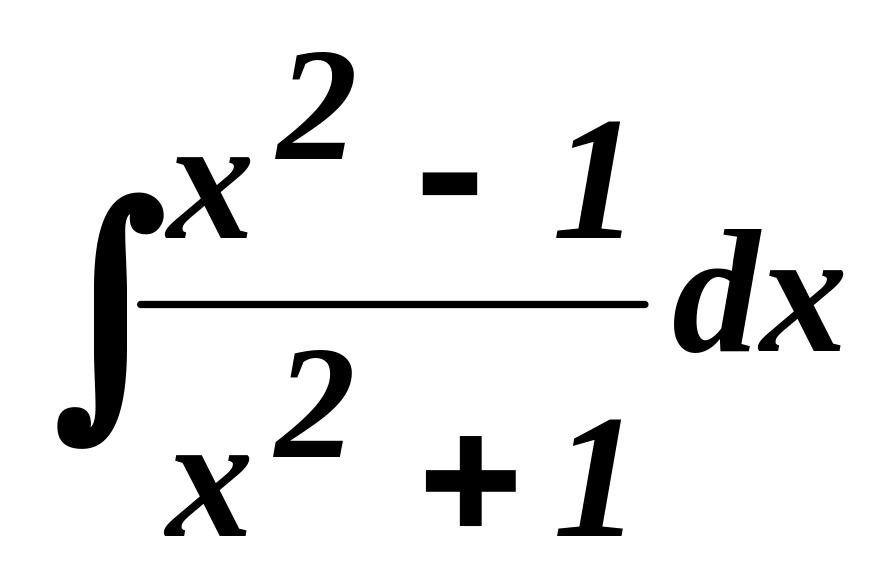 равен:
равен:Интеграл
 равен:
равен:2/3
-1
3/2
0
-2/3
Интеграл
 равен:
равен:7/3
-26/3
13/3
114
26/3
Определенный интеграл
 равен:
равен:1040
1
-5
1035
2
Определенный интеграл
 равен:
равен:10е4
10
20е2
0
30е2
Определенный интеграл
 равен:
равен:1
0
3

2
Определенный интеграл
 равен:
равен:2e4
6+e4
0
6+2e4
e4-e-4
Несобственный интеграл
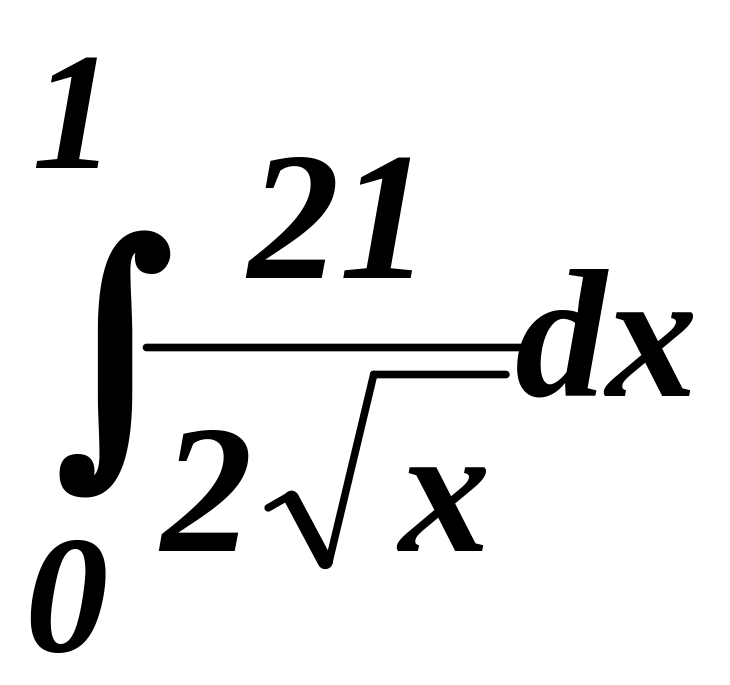 равен:
равен:0
1
2
21
Несобственный интеграл
 равен:
равен:5
0
1
-1
Найти площадь фигуры, ограниченной кривыми
 и
и
 .
.4,5
3,5
2,5
1,5
0,5
Найти с точностью до двух знаков после запятой площадь фигуры, ограниченной кривыми и
 .
.2,27
2,47
2,57
2,67
2,77
