2.10. Некоторые геометрические приложения определенного интеграла

I. Вычисление площади плоской фигуры

1) Площадь криволинейной трапеции (см. рис. 5), ограниченной кривой y =f(x) , прямыми _, и отрезком оси , вычисляется по формуле .

П ример. Вычислить площадь фигуры (см. рис.6), ограниченной кубической параболой , прямой и осью .

Решение. (кв.ед.).

2 ) Площадь криволинейной трапеции, ограниченной кривой _, прямыми и отрезком оси , вычисляется по той же формуле, что и при _, но определенный интеграл будет равен отрицательному числу. В этом случае площадь криволинейной трапеции численно равна абсолютной величине этого числа, а знак минус означает, что трапеция расположена ниже оси , то есть .

3) Если график непрерывной функции пересекает ось несколько раз, например, в точках (см. рис. 8), то площадь плоской фигуры, ограниченной графиком данной функции, прямыми и осью , вычисляется по формуле.

Пример. Вычислить площадь фигуры (см. рис. 9), ограниченной линиями , и .

Решение. Парабола пересекает ось в двух точках с абсциссами 0 и 1, так как если , то , следовательно, , или . Тогда

4) Если плоская фигура ограничена снизу и сверху графиками функций и , , , где , – две непрерывные функции. Тогда площадь данной фигуры равна:

.

Пример. Вычислить площадь фигуры (см. рис. 10), ограниченной графиками функций и .

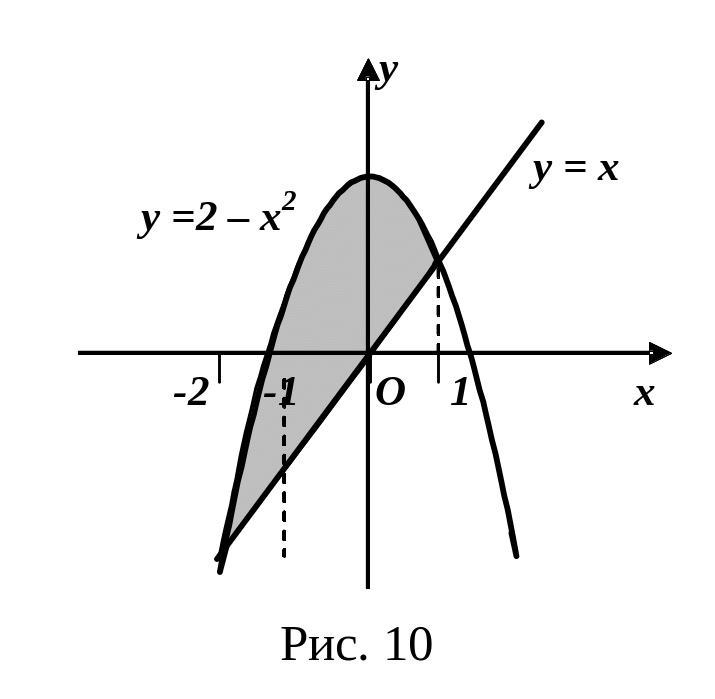Р ешение. Найдем абсциссы точек пересечения прямой с параболой . Решая систему , получаем, что , .

Подставляем найденные пределы интегрирования и функции в формулу: S= (кв.ед.).

5) Площадь криволинейной трапеции в случае, когда верхняя граница задана параметрическими уравнениями , , , причем , находится по формуле , которая получена из формулы заменой переменных.

Пример. Вычислить площадь плоской фигуры (см. рис. 11), ограниченной одной аркой циклоиды и осью .

Р ешение. Так как , то , а изменяется от до . Следовательно,

(кв. ед.).

6

α

) Площадь криволинейного сектора (см. рис.12), ограниченного кривой, заданной в полярных координатах уравнением , , – непрерывная функция, на отрезке находится по формуле .

Пример. Вычислить площадь плоской фигуры, ограниченной лемнискатой (см. рис. 13).

Р ешение. Пусть . Четвертой части искомой площади соответствует изменение от 0 до , следовательно,

II. Вычисление длины дуги плоской кривой

1) Пусть дуга кривой задана уравнением , где – непрерывно дифференцируемая функция. Тогда длина дуги вычисляется по формуле .

Пример. Найти длину окружности (см. рис. 14).

Р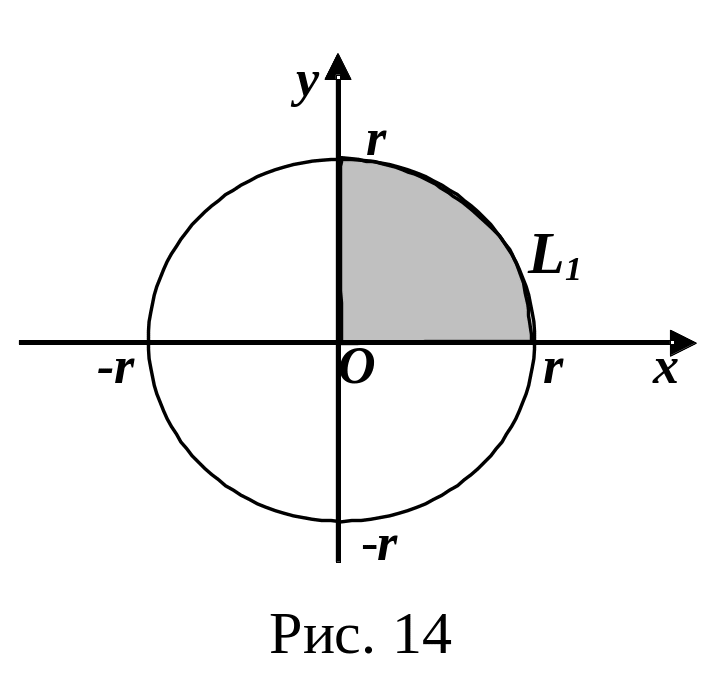 ешение. Вычислим часть длины окружности. Уравнение дуги , лежащей в первом квадранте будет иметь вид . Следовательно, . Тогда

.

2) В случае, когда кривая задана параметрическими уравнениями , , где – непрерывно дифференцируемые функции, длина дуги вычисляется по формуле .

Здесь – значения параметра , соответствующие концам дуги и .

Пример. Найти длину дуги кривой от до .

Решение. Найдем производные по параметру :

. Тогда

=

= .

3) Если кривая задана в полярных координатах уравнением , , то длина дуги .

Пример. Найти длину дуги кривой от до .

Решение. . Следовательно,

= .