2. Определенный интеграл

2.1. Понятие определенного интеграла

П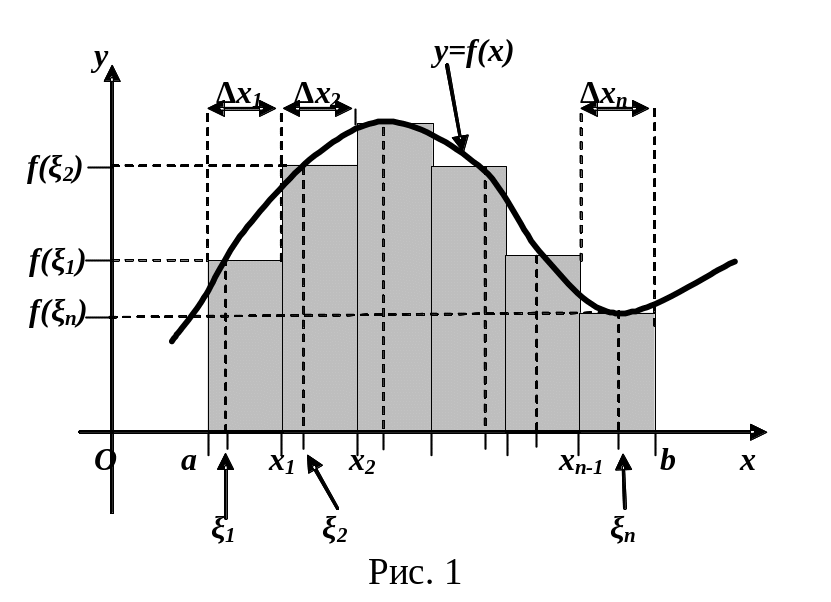 усть функция определена на отрезке . Разобьем произвольным образом этот отрезок точками на частичных отрезков длиной . Выберем в каждой из них точку _, . Сумма вида называется _– ой интегральной суммой функции на отрезке . Геометрически сумма представляет собой алгебраическую сумму площадей прямоугольников, заштрихованных на рис. 1, в основании которых лежат частичные отрезки , а высоты равны .

Определение. Предел интегральной суммы , найденный при условии, что длина наибольшего частичного отрезка стремится к нулю (если этот предел существует и конечен) называется определенным интегралом от функции по отрезку и обозначается , т.е. по определению

.

Функция называется подынтегральной функцией, – подынтегральным выражением, a, b – соответственно нижним и верхним пределами интегрирования, x – переменной интегрирования.

Теорема. Если функция непрерывна на отрезке , то она интегрируема на , т.е. предел интегральной суммы существует и не зависит от способа разбиения отрезка на частичные отрезки и выбора на них точек .

Следствие. Кусочно-непрерывная на отрезке функция интегрируема на этом отрезке.

2.2. Геометрический смысл определенного интеграла

Если , , то геометрически определенный интеграл выражает площадь фигуры, ограниченной графиком функции , осью и двумя прямыми (см. рис. 2). Эта фигура называется криволинейной трапецией.

В общем случае, когда функция на отрезке принимает значения разных знаков, определенный интеграл выражает разность площадей криволинейных трапеций, расположенных над осью и под ней, так как площадям криволинейных трапеций, расположенных под осью присваивается знак " - ".

2.3. Основные свойства определенного интеграла

. . . .

. . . .

. . . .

.

.

(Здесь и далее предполагается, что указанные интегралы существуют).

2.4. Оценки интегралов. Формула среднего значения

. Если на и , то .

. Если на и , то .

. Если , и , то .

Теорема (теорема о среднем). Если функция непрерывна на , то на этом отрезке существует точка с такая, что

. (2.1.)

Р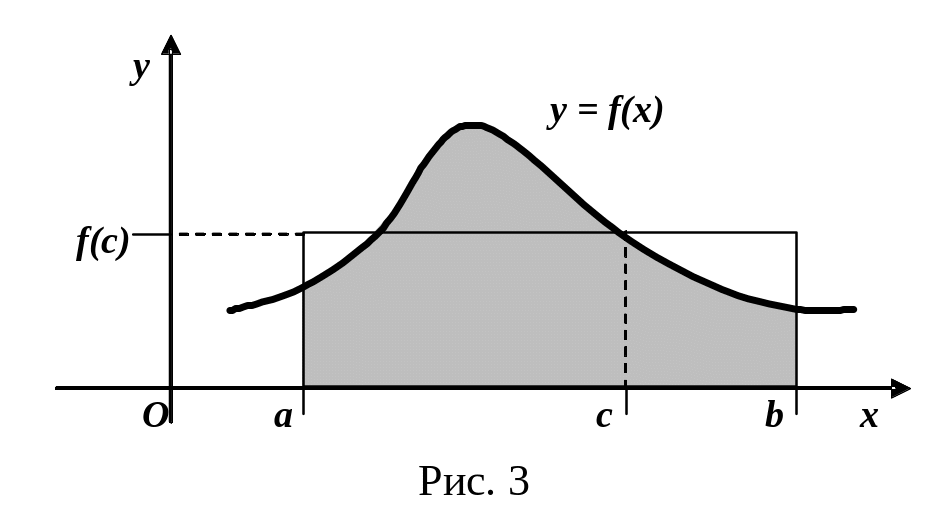 авенство (2.1.) называется формулой среднего значения, а величина – средним значением на .

Замечание. Геометрический смысл теоремы заключается в том, что величина определенного интеграла при равна площади прямоугольника, имеющего высоту и основание (b – a) (см. рис.3).

2.5. Связь между определенным и неопределенным интегралом. Интеграл с переменным верхним пределом

О пределение. Функция , аргументом которой является верхний предел определенного интеграла называют интегралом с переменным верхним пределом.

Замечание. Геометрически функция представляет собой площадь заштрихованной на рис. 4 криволинейной трапеции, если .

Теорема. Производная интеграла от непрерывной функции по переменному верхнему пределу существует и равна значению подынтегральной функции в точке x, равной верхнему пределу, т.е.

. (2.2)

Следствие. Интеграл с переменным верхним пределом является первообразной для непрерывной функции на отрезке .

Так как всякая другая первообразная может отличаться от только на постоянную, то из следствия следует связь между неопределенным и определенным интегралом: .