Модуль 5 функция нескольких переменных

1. Понятие функции нескольких переменных

Определение. Если каждой упорядоченной паре действительных чисел из некоторой области по определенному правилу ставится в соответствие определенное число , то говорят, что на множестве задана функция двух переменных и . При этом пишут или

: ® , где - закон соответствия.

Пример 1: - площадь прямоугольника со сторонами, длины которых равны и .

Определение. Множество называется областью определения функции и обозначается: , множество - областью значений, и - независимыми переменными или аргументами.

Определение. Графиком функции двух переменных называют поверхность, образованную множеством точек пространства, координаты которых удовлетворяют уравнению .

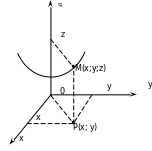
Пара значений и определяет на плоскости точку , а - аппликату соответствующей точки на поверхности (рис.2).

Говорят, что есть функция точки и обозначают .

Пример 2. Найти область определения функции .

Решение. Эта функция определена, если , т.е. . Областью определения функции является часть плоскости, заключенная между двумя прямыми и .

Пример 3: Найти область определения функции и построить в плоскости .

Решение. Для того чтобы имело действительное значение, необходимо выполнение условия или .

В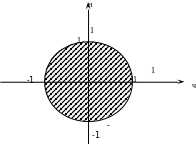 се точки , координаты которых удовлетворяют последнему неравенству, лежат в круге радиуса 1 с центром в начале координат и на границе этого круга (рис.1).

Рис.1 Рис.2

Таким образом ={ }.

Определение. Линией уровня функции называется линия на плоскости , в точках которой функция сохраняет постоянное значение .

Определение. Поверхностью уровня функции называется по-верхность , в точках которой функция сохраняет постоянное значение .

Пример 4. Найти поверхности уровня функции .

Решение. Уравнение семейства поверхностей уровня имеет вид . Поверхности уровня являются плоскостями с нормальным вектором ={1,1,3}.

Пример 5. Найти линии уровня функции .

Решение. Уравнение семейства линий уровня имеет вид . Придавая различные действительные значения, получим окружности с центром в начале координат.

Замечание. Определение функции двух переменных легко обобщается на случай трех и большего числа переменных.

Определение. Пусть - множество упорядоченных систем чисел, - заданное натуральное число; - числовое множество. Если каждой такой системе соответствует в силу некоторого определенного закона число , то говорят, что на задана функция -переменных , при этом пишут: .

2. Предел и непрерывность функции двух переменных

Определение. Число А называется пределом функции в точке , если для любого e > 0 существует d > 0, такое, что при всех удовлетворяющих условиям и справедливо неравенство

|.

Если А - предел функции в точке , то символически это записывается в виде: .

Пример. Вычислить .

Решение: т.к. .

Определение. Функция называется непрерывной в точке , если справедливо равенство .

Например, функция непрерывна в любой точке плоскости, за исключением точки , в которой функция терпит разрыв.

Определение. Функция, непрерывная во всех точках некоторой области D, называется непрерывной в данной области.

Так же как для функции одной переменной, используя данные определения и теоремы о пределах можно доказать, что арифметические операции над непрерывными функциями и построение сложных функций из непрерывных функций приводит к непрерывным функциям.