Тема 3.7.Логарифмическая функция, её свойства и график

Цели урока:

Образовательные: 1. Ввести понятие логарифмической функции, дать определение.

2. Изучить основные свойства логарифмической функции.

3. Сформировать умение выполнять построение графика логарифмической функции.

Развивающие: 1. Формировать графическую и функциональную культуру учащихся.

Воспитательные: 1. Воспитывать ответственное отношение к труду.

3. Показать взаимосвязь математики с окружающей действительностью.

Оборудование: компьютер, мультимедийная установка, авторская презентация к уроку, учебник «Алгебра и начала анализа 11 класс»

Ход урока.

1.Орг. Момент

2. Проверка домашнего задания

3. Актуализация.

Сформулируйте определение функции.

Назвать функции, заданные формулами и соответствующие им графики.

Назвать основные этапы исследования свойств функции.

Сформулируйте определение логарифма.

Вычислите: (задание по вариантам, работают все, взаимопроверка)

1 вариант.

2 Вариант.

4. Изложение нового материала. «Логарифмическая любовь»

На плакате (доске) изображены графики показательной и логарифмической функций

-Любовь зла, полюбишь и козла, - сказал логарифм и печально затих в самом начале оси Х

-Да, и кто же этот козел? Вернее коза?- спросил аргумент Х

Логарифм глубоко вздохнул:

-Показательная функция… Не понимаю, чего хорошего ты нашел в ней? Да ты посмотри на кривую ее поведения!

- А что кривая? У меня ведь тоже вон как крутизна-то меняется.

- Ну, ты совсем другое дело, ты ведь мужчина! Да ладно, я помогу тебе.

А в это время показательная функция беззаботно прогуливалась где-то в самой отрицательной части оси ОХ, она даже не думала, что в четвертом квадрате кто-то сильно страдает по ней, такая уж она была легкомысленная, эта показательная функция.

Аргумент Х стал возрастать, логарифм нехотя пополз вдоль оси ОУ навстречу показательной функции, которая в то время находилась в точке А(0;1),и эта точка, подслушав разговор логарифма и аргумента Х, все разболтала ей. Показательная функция заинтересовалась логарифмом и даже стала приближаться к нему, но им так и не суждено было встретиться; злая и завистливая линейная зависимость, которая уже давно охотилась за бедным логарифмом, встала между ними.

Показательная функция, видя, что логарифм не один, круто повернула верхи умчалась к еще не покоренному У. Таковы женщины! Они безразличны к тем, кто их любит, и любят тех, кто к ним безразличен. Сердце логарифма было разбито. Он, даже не посмотрев на повторную линейную зависимость, ушел на веки к бесконечности, которая хоть и не была такой красивой и подвижной как показательная функция, но всегда делила с ним любое горе и любую радость. Хотя радости в жизни неудачника логарифма было очень и очень мало, да и не в этом счастье.

Аргумент Х похлопал друга по плечу и сказал:

-Не огорчайся, друг, ведь даже и в каплях слез отражается солнце, помнишь, что сказал Шекспир: «Непостоянство – имя твое, женщина, даже если ты являешься математической функцией»

Итак, тема нашего сегодняшнего занятия…(студенты озвучивают название темы)

Задание 1.

Обозначьте изменяющуюся величину через x. Обозначьте его через y значение логарифма.

Задайте формулой полученную зависимость y от x (проверяем результаты каждого варианта). Записываем на доске: y=log ₂ x, y=log _1/2 x

Задаются ли этими формулами функции? Подумайте, как бы вы назвали эту функцию? (Эту функцию называют логарифмической)

Объявляется тема урока с записью в тетрадях.

Вопрос. Какую же функцию мы назовём логарифмической? (даётся определение логарифмической функции).

Логарифмической называется функция вида у = log_a x, где а – заданное число, а > 0, а ≠ 1.

Рассмотрим свойства логарифмической функции.

1) Областью определения логарифмической функции является множество всех положительных чисел.

Это утверждение следует из определения логарифма, так как только при х > 0 выражение log_a x имеем смысл.

2) Множество значений логарифмической функции представлено множеством R всех действительных чисел.

Это утверждение следует из того, что для любого числа b (b – действительное чсило) есть такое положительное число х, что log_a x = b, т.е. уравнение log_a x = b имеет корень. Такой корень существует; он равен х = а^b, так как log_a а^b = b.

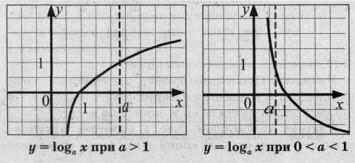
3) Логарифмическая функция у = log_a x является возрастающей на промежутке х > 0, если а > 1,

и убывающей, если 0 < а < 1.

4) Если а > 1, то при х > 1 функция у = log_a x принимает положительные значения, при при 0 < х < 1 – отрицательные.

Если 0 < а < 1, то функция у = log_a x принимает положительные значения при 0 < х < 1, отрицательные – при х > 1.

Отметим, что график любой логарифмической функции у = log_a x проходит через точку (1; 0).

При решении уравнений часто используется теорема: если log_a х₁ = log_a х₂, где а > 0, а ≠ 1, х₁ > 0, х₂ >0, то х₁ = х₂.

Рассмотрим несколько задач.

Задача 1.

Решить уравнение log₅ (3х– 2) = log₅ 7.

Решение.

Используя доказанную теорему, получаем 3х – 2 = 7, откуда 3х = 9, х = 3.

Ответ. х = 3.

Задача 2.

Решить неравенство log₂ х < 3.

Решение.

Пользуясь тем, что 3 = log₂ 2³ = log₂ 8, запишем данное неравенство так: log₂ х < log₂ 8.

Так как функция у = log₂ х определена при х > 0 и возрастает, то неравенство log₂ х < log₂ 8 выполняется при  х > 0 и х < 8.

Ответ. 0 < х < 8.

Задача 3.

Решить неравенство log_1/3 х ≤ -2.

Решение.

Запишем данное неравенство таким образом: log_1/3 х ≤ log_1/3 9. Функция у = log_1/3 х определена при х ≥ 0 и убывает, поэтому неравенство выполняется при х > 0 и х ≥ 9.

Ответ. х ≥ 9.

Задание 2. Построить графики функций y=log ₂ x и y=log _1/2 x

Задание 3. Используя свойства логарифмов, по построенным графикам сформулируйте основные свойства логарифмической функции.