МИНИСТЕРСВО СЕЛЬСКОГО ХОЗЯЙСТВА РФ

ФГБОУ ВПО “Великолукская государственная сельскохозяйственная академия”

Инженерный факультет

Кафедра “Автомобили, тракторы и сельскохозяйственные машины”

КОНТРОЛЬНАЯ РАБОТА

по дисциплине “Теплотехника”

«Расчёт циклов поршневых двигателей внутреннего сгорания»

Выполнил: студент ЭЛ 31 группы

Двойнев Д.Н

Принял: преподаватель

Максимов Н.М.

Великие Луки

2012

Исходные данные для расчёта

Рабочее тело обладает свойствами:

а) газовая смесь по массе - ; ; ;

б) давление в начале сжатия -

в) температура в начале сжатия -

г) степень сжатия двигателя -

д) степень повышения давления -

е) степень предварительного расширения -

ж) количество подведённой теплоты -

1. Изображение цикла в P-ν и T-s-диаграммах и указание термодинамических процессов, из которых он состоит.

Так как из исходных данных известно, что степень предварительного расширения ρ=1,6 и степень повышения давления λ=1,2, то это свидетельствует о том, что рассматриваемый мною цикл – это цикл Тринклера (цикл со смешанным подводом теплоты).

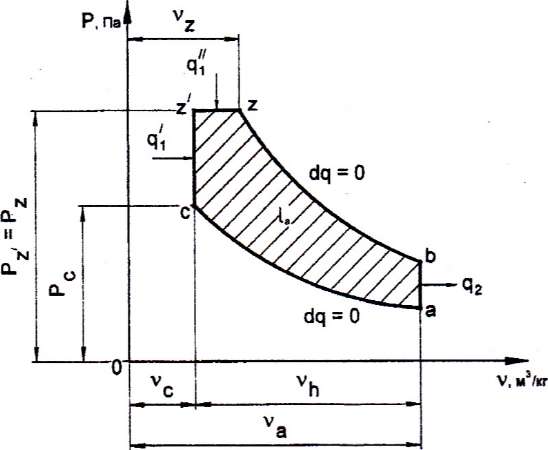
Рисунок 1 - Диаграмма цикла двигателя внутреннего сгорания со смешанным подводом теплоты, при ν=const и P=const в P-ν- координатах

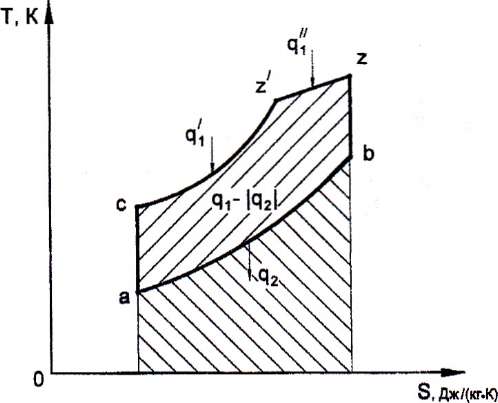
Рисунок 2 - Диаграмма цикла двигателя внутреннего сгорания со смешанным подводом теплоты, при ν=const и P=const в T-s- координатах

Цикл двигателя внутреннего сгорания со смешанным подводом теплоты состоит из следующих термодинамических процессов:

ac – адиабатное сжатие рабочего тела;

cz’ – изохорный подвод теплоты при ν=const (в реальном двигателе сжигание топлива);

z’z – изобарный подвод теплоты при p=const (в реальном двигателе досжигание топлива);

zb – адиабатное расширение рабочего тела;

ba – изохорный отвод теплоты в охладитель.

2. Определение параметров рабочего тела в характерных точках цикла.

Для определения параметров рабочего тела, определю сначала:

- газовую постоянную для смеси R, Дж/(кг К);

- коэффициент Пуассона, показатель адиабаты смеси K.

Газовую постоянную смеси можно найти из формулы

(1)

, (2)

где - универсальная газовая постоянная ( =8314 Дж/(кмоль К));

- молярная масса смеси и компонента, кг/кмоль (таблица А.1 (Приложение А));

(3)

Подставляя известные значения величины в формулу (1), получаю

(4)

Теперь найду молярную массу, подставив данные в выражение (3)

Определение показателя адиабаты K

, (5)

где и - массовые теплоёмкости смеси кДж/(кг К)

, (6)

, (7)

где и - массовые теплоёмкости компонентов смеси, Дж/(кг К)

- массовая доля компонентов в смеси.

, (8)

, (9)

, (10)

где - показатель адиабаты компонента (таблица А.1 (Приложение А));

- газовая постоянная компонента, кДж/(кг К).

Из таблицы А.1 (Приложение А) нахожу показатель – К для каждого компонента смеси: K ; K ; K ; K

Подставляя известные величины в формулы (9) и (10), получаю

Теперь нахожу и

(11)

Зная и , найду К

Определяю параметры в характерных точках цикла (рисунок 1).

Параметры точки «а»:

Удельный объём точки «а», найду из формулы

(13)

Параметры точки «с»:

(14)

(15)

(16)

Параметры точки «z’»:

(17)

(18)

Параметры точки «z»:

(19)

(20)

Параметры точки «b»:

(21)

(22)

3. Определение термического КПД двигателя через параметры цикла.

Термический КПД для цикла со смешанным подводом теплоты определяется по формуле

(23)

Подставляя известные значения в формулу (23), получаю

или

4. Определение количества подведённой и отведённой теплоты.

Определяю количество подведённой теплоты, кДж/кг, по формуле

(24)

где

- теплота, подведённая по изобаре, кДж/кг.

Подставляя известные величины в формулу (24), получаю

Определяю количество отведённой теплоты ( , кДж/кг) по формуле

(25)

.

5. Сравнение расчётного термического КПД с его значением, определённым через подведённую и отведённую теплоту, а так же с КПД цикла Карно

Термический КПД цикла через подведённую и отведённую теплоту определяется по формуле

(26)

Подставляя известные величины в формулу (26), получаю

или =61,8%.

Термический КПД цикла Карно нахожу по формуле

(27)

где и - минимальная и максимальная температура цикла, К.

Подставляя известные величины в формулу (27), получаю

или .

Сравниваю полученные КПД:

; (28)

0,618=0,618<0,816.

6. Определяю работу по процессам цикла и суммарную работу за цикл

Так как процесс (a-с) адиабатный, то работа определяется по формуле

(29)

Подставляя известные значения в формулу, получаю

Так как процесс (c-z’) изохорный, то ,

Процесс (z’-z) изобарный, и работа определяется по формуле

(30)

Процесс (z-b) адиабатный, как и процесс (a-c). Поэтому, справедлива формула

(31)

Процесс (b-a) изохорный, значит .

Работа за цикл будет складываться из всех работ процессов цикла по формуле

(32)

.