Функции полезности

В данном разделе рассмотрены три функции полезнос­ти, основанные на понятиях независимости по предпочтению и независимости по полезности критериев. Прежде чем перехо­дить к рассмотрению конкретных функций, введём некоторые обозначения.

Для каждого критерия k_j(j=1,…,т)определим области определения: – наименее предпочтительное из допустимых значений: – наиболее предпочтительное значение. В зависимости от содержания критерия в качестве может быть минимально допустимое значение (примером такого критерия является тактовая частота процессора ПЭВМ) или максимальное из допустимых (стоимость ПЭВМ). Также и может быть максимальным или минимальным значением критерия.

Таким образом, каждый критерий изменяется в интервале .

Функция полезности U(k₁,..., k_m) изменяется в интервале[0;1],причем ,a .

Будем обозначать через (отрицаниеk_j) подмножество критериев {k₁,...,k_j-1,k_j+1,...,k_m}, т.е. всё множество за исключени­емk_j. Аналогично,подмножество, не включающее k_j и k_i. Подмножество будем называть дополнением критерияk_j,aподмножество–дополнением пары критериев k_j и k_i.С учётом введённых обозначений следующие записи функции полезности идентичны:

.

Запись означает, что критерий , а все остальные .

В последующих пунктах данного раздела будут рассмотре­ны полилинейная, мультипликативная и аддитивная функции полезности. Для каждой функции будут сформулированы условия её существования, т.е. условия, когда она может обоснованно использоваться, а также изложены вопросы определения её параметров.

Полилинейная функция полезности

Прежде чем переходить к рассмотрению условий сущес­твования полилинейной функции, введём определение независи­мости критерия от своего дополнения.

Определение 3.1.Критерийk_jнезависим по полезности от своего дополнения ,если функция полезности представляется в виде

,(3.1)

где – функция от дополненияk_j.

Поясним содержательный смысл (3.1). Для этого постро­им функцию полезности в зависимости от одного критерия k_j (рис.3.1).Это не что иное, как условная функция полезности при фиксированном дополнении. Условная функцияизменяется в интервале [;].

Перейдём к другой условной функции полезности, поменяв значения критериев, входящих в дополнение, на.

На рис.3.1изображена и вторая условная функция с ин­тервалом изменения [;].

Условие (3.1) означает, что две любые условные функции полезности связаны между собой положительным линейным преобразованием. Действительно,

Откуда

, где; .

Сучетом вышеприведён­ной интерпретации условия (3.1), проверка независимости по полезности критерия от своего дополнения достаточно проста. Для этого необхо­димо зафиксировать дополне­ние, например ,и по­строить условную функцию полезности от одного крите­рия, приняв, а (рис.3.2).Назо­вём такую функциюнормиро­ванной условной функцией полезности.

Нормированная условная функция должна отражать из­менения предпочтения многокритериального объекта при изме­нении только одного критерия.

Поменяв значения критериев, входящих в дополнение на ,вновь построим нормированную условную функцию. Если эта функция не изменяется при изменении дополнения, то, значит, выполняется условие независимости по полезности критерия от своего дополнения. Тогда нормированная условная функция полезности не зависит от ,поэтому её будем обозначать U_j(k_j).

Рассмотрим сначала полилинейную функцию полезности для случая двух критериев k₁иk₂.

Теорема 3.1.Еслиk₁независим по полезности отk₂, а k₂ – отk₁, то функция полезности имеет вид

U( k₁,k₂ ) = W₁U₁( k₁ ) + W₂U₂( k₂ ) + (1 - W₁ - W₂ )U₁( k₁ )U₂( k₂ ), (3.2)

где U₁(k₁), U₂(k₂) – нормированные условные функции полез­ности;W₁,W₂ – шкалирующие коэффициенты.

Доказательство.Из условия независимости по полезностиk₁отk₂ следует:

.(3.3)

При это условие запишется в виде

.

Откуда следует

(3.4)

Подставляя (3.4)в (3.3),получим

(3.5)

Используя условия независимости по полезности k₂ отk₁, аналогично получим

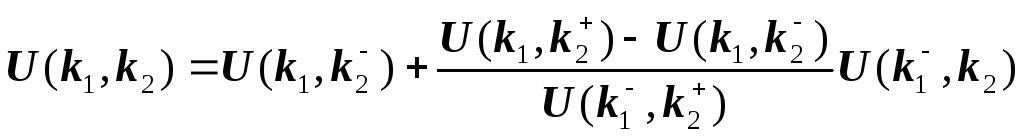(3.6)

Введём в рассмотрение шкалирующие коэффициенты:

(3.7)

Тогда , гдеU₁(k₁), U₂(k₂)– нормированные условные функции полезности.

С учётом введённых шкалирующих коэффициентов (3.5) и (3.6) примут вид

; (3.8)

. (3.9)

Используя (3.9),определим

Подставляя последнее выражение в (3.8),после упрощения получим искомое (3.2).

Параметры полилинейной функции полезности.Чтобы использовать функцию (3.2) на практике, необходимо:

а) построить нормированные условные функции полезности U₁(k₁), U₂(k₂)и убедиться, что они независимы;

б) задать шкалирующие коэффициенты W₁ и W₂, для этого ЛПР необходимо оценить «псевдообъекты», представленные в табл.3.1.

Лицо, принимающее решение, сравнивая с объектами В⁺ иВ^-, имеющими соответственно оценки 1.0и 0.0,должно дать оценки псевдообъектов, которые и являются коэффициентамиW₁, W₂.

Таблица 3.1

Определение шкалирующих коэффициентов

Оцениваемые объекты	k1	k2	Оценки объектов
Объект В+			1.0
Псевдообъект В1			W1
Псевдообъект В2			W2
Объект В-			0.0

Сформулируем теорему о существовании полилинейной функции полезности для трёх критериев: k₁, k₂ иk₃.

Теорема 3.2.Пусть каждый из трёх критериев независим по полезности от своего дополнения, тогда функция полезности имеет вид

,(3.10)

где U_j(k_j) (j=1,2,3)–нормированные условные функции полезности;W_j, W_j,i, W_1,2,3– постоянные коэффициенты. Причем

Доказательство данной теоремы приведено в соответствующей литературе. Отметим, что для определения всех коэффициентовW_j для случая трёх критериев ЛПР должно давать оценку уже шести псевдообъектов.

Теорему 3.2можно обобщить на случайт>3 критериев.

Теорема 3.3.Пусть каждый из критериевk_j(j=1,…, т) независим по полезности от своего дополнения, тогда функция полезности имеет вид

,

где U_j(k_j) – нормированные условные функции полезности,

Из вида полилинейной функции следует, что при большом числе критериев она имеет значительное количество коэффици­ентов, для определения которых требуется от ЛПР много оценок псевдообъектов. Поэтому при т>4ее использование затруднительно.