РЕШЕНИЕ МНОГОКРИТЕРИАЛЬНЫХ ЗАДАЧ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ

При решении практических задач часто возникают ситуации, когда для некоторых объектов отсутствуют данные по одному или нескольким единичным критериям, т.е. имеет место неопределенность в смысле исходных данных для оценки и выбора объектов. В некоторых случаях восполнить недостающие данные можно с привлечением экспертов, т.е. задать ожидаемые значения критериев.

Вместе с тем, отсутствующие данные можно определять, используя определённые принципы, подобные известным критериям выбора решений в условиях неопределённости: Вальда, Гурвица, Лапласа. Причём такие принципы можно использовать как по отношению к отдельным критери­ям, чтобы получить отдельное значение, так и по отношению к интегральным оценкам всего объекта, чтобы выбрать наиболее предпочтительный. Остановимся на каждом из этих подходов отдельно.

Суть первого подхода в том, чтобы определить неизвестное значение критерия для одного объекта на основе определённого принципа.

В табл.5.1 приведён пример, в котором для первого объекта нет данных k₁ и k₂, а для второго объекта отсутствуют данные по k₂.

Числом (-1) в таблице обозначен факт отсутствия данных. Ставится задача внесения в таблицу недостающих данных, т.е. замены -1 на численные значения.

Обозначим через k_1,s (s=l,…,n₁) возможные значения, которые может принимать критерий k₁. Для качественных критериев число возможных значений, как правило, невелико. Пусть – наиболее предпочтительное из k_1,s значение, a – наименее предпочтительное.

Таблица 5.1

Исходные данные МКЗ в условиях неопределенности

Варианты	k1	k2	k3	k4
B1	-1		-1
B2		-1
B3

Аналогично k_2,s (s=l,…,n₂) – возможные значения k₂; k_3,s (s=l,...,n₃) – возможные значения k₃.

В качестве принципов определения недостающих данных можно использовать:

а) пессимистический принцип (аналогия – критерий Вальда), тогда (-1) заменяется на , т.е. ЛПР ориентируется на самое худшее значение критерия;

б) оптимистический принцип, тогда (-1) заменяется на ;

в) сочетание оптимистического и пессимистического принципов (аналогия – критерий Гурвица). В этом случае (-1) заменяется на значение, вычисляемое в соответствии с выражением

,

где α(0;1) – коэффициент оптимизма, задающийся ЛПР, исходя из принятого им риска;

г) принцип среднего из возможных (аналогия – критерий Лапласа), тогда (-1) заменяется на

.

К приведённым принципам, описанным в литературе, можно добавить ещё один, основанный на использовании операторов агрегирования, назовем его принципом учета риска.

д) принцип учёта риска. Определение производится в следующей последовательности:

переход к безразмерным величинам

,

при этом получим, что ;

агрегирование по s=l,…,n_j с использованием операто­ров, квазиконъюнктивного (если ЛПР не желает рисковать) или квазидизъюнктивного (если ЛПР хочет рисковать).

Для лучшей интерпрета­ции параметра жесткости λ, который определяет степень риска, рекомендуется исполь­зовать симметричный опера­тор. Пример генерирующих функций для такого операто­ра приведен на рис.5.1.

Вид генерирующих функ­ций одинаков. φ(x) задается указанием величины a_φ и радиусом R_φ, а ψ(x) – соот­ветственно a_ψ и R_ψ. Рекомен­дуется значения радиусов задавать одинаковыми. Пара­метром жесткости оператора будет λ = a_ψ - a_φ. В качестве коэффициентов V_j в операторе следует использовать 1/n_j;

обратный переход от безразмерных величин к размерностям критерия:

.

При a_φ = 0,5 и a_ψ = 0,5 оператор агрегирования становится аддитивным и данный принцип переходит в принцип среднего.

Достоинством данного принципа по сравнению с принци­пом (в) состоит в том, что учитываются все значения и даже их распределение.

После задания ЛПР принципа определения неизвестных данных все (-1) заменяются конкретными значениями и задача переходит в класс полностью определённых МКЗ. Данный подход может быть использован как при использовании интерактивных методов, так и при оценке объектов по интегральному критерию (при использовании функций полезности или операторов агрегирования).

Рассмотрим второй подход к выбору объектов в условиях неопределённости. Смысл его в том, что сравнение и выбор наиболее предпочтительного варианта осуществляются на основе интегральной оценки объекта, даже при отсутствии данных по отдельным критериям.

Для того чтобы иметь возможность вычисления интеграль­ной оценки объекта, необходимо задать процедуру ее вычисле­ния либо на основе функции полезности, либо на основе агрегирования по многоуровневой системе критериев.

Пусть имеем функцию полезности U(k₁,k₂,k₃,k₄).

В варианте 2 табл.5.1 отсутствуют данные по критерию k₂. Возможное множество вариантов B^2,s (s=l,…,n₂), получаемое из B², представлено в табл.5.2.

Таблица 5.2

Возможные варианты объекта при неопределенности критерия k2

Варианты	k1	k2	k3	k4	U2,s
B2,1		K2,1			u2,1
B2,2		k2,2			U2,2
…	…	…	…	…	…

Для варианта 1 (см. табл.5.1), по которому неизвестны значения k₁ и k₃ возможное множество B¹ будет содержать n₁∙n₃ вариантов.

Таким образом, на основе каждого объекта, имеющего неопределенность по одному или нескольким критериям, генерируется множество возможных вариантов.

Имея функцию полезности U(k₁,k₂,k₃,k₄), можем сделать оценку каждого из возможных вариантов u^1,s (s=l,…, n₁∙n₃), u^2,s (s=l,…,n₂).

Используя вычисленные значения u^2,s (s=l,…,n₂), можем применить описанные в первом подходе принципы для оценки объекта В²:

а) пессимистический принцип:

, в примере ;

б) оптимистический принцип:

, в примере .

Для приведённых выше принципов нет необходимости генерировать все возможные варианты, так как получается, если вместо неизвестных значений критериев подставить минимальные по предпочтению , a получается подстановкой максимальных по предпочтению значений ;

в) сочетание пессимистического и оптимистического принципов:

,

где α – коэффициент оптимизма;

г) принцип среднего из возможных:

.

К перечисленным принципам следует добавить ещё три:

д) принцип среднего и среднеквадратического:

,

где , а r > 0 – коэффициент риска, задаваемый ЛПР.

При r = 0 данный принцип переходит в принцип среднего. Если r > 0, то ЛПР рискует, завышая среднюю оценку, однако он действительно может получить объект с большей, чем средняя, оценкой полезности. Чем больше r, тем больше риск.

Рекомендуется использовать r в интервале [0;1], так как для объектов, не имеющих неопределенности в значениях критериев, D(u^i,s) равна 0, что равнозначно r = 0, и, значит, при r > 1 оценки объектов, имеющих неопределенность, будут сущес­твенно завышаться:

е) принцип наиболее вероятного значения.

Чтобы использовать данный принцип, необходимо построить распределение значений u^i,s (s=l,…,n_i) в виде гистограммы, пример которой приведён на рис.5.2.

В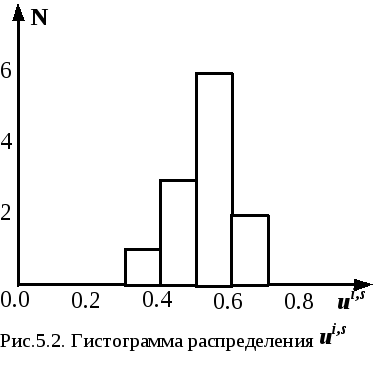 интервал (0,5;0,6) по­пало шесть значений u^i,s из 12 (50%), т.е. этот интервал содержит наиболее вероятное значение uⁱ. Наиболее веро­ятное значение вычислим как среднее из попавших в интервал (0,5;0,6) u^i,s и при­мем его за оценку uⁱ. Дру­гими словами, необходимо выбрать интервал, в который попадает около половины всех значений u^i,s, и где они менее всего отличаются друг от друга, а затем усреднить эти значения.

Самый простой подход к формированию данного интер­вала – исключение 25% максимальных (справа) и 25% мини­мальных (слева) значений u^i,s. Оставшиеся 50% значений следует усреднить, после чего и получим оценку объекта в условиях неопределённости;

ж) принцип учёта риска, основанный на использовании операторов агрегирования. Для оценки вариантов в условиях неопределённости можно использовать квазиконъюнктивные или квазидизъюнктивные операторы, причём все u^i,s (s=l,…,n_i) равнозначны, т.е. V_i = 1/n_i. Используя квазиконъ­юнктивные операторы, ЛПР не рискует. При применении квазидизъюнктивных операторов ЛПР рискует. Степень риска определяется коэффициентом жёсткости соответствующего оператора. Набор операторов агрегирования тот же, что и в принципе (д) при определении недостающих данных в первом подходе.

Какой из подходов и какой принцип выбрать при разрешении неопределённости значений критериев, должно решать ЛПР. Целесообразно использовать несколько принципов, поочередно решая задачу для каждого из них. Решение, более устойчивое к выбору подхода и принципу снятия неопределённости, следует рассматривать как наиболее предпо­чтительное.

Разделы.

Многокритериальные задачи

Интерактивные методы решения МКЗ

Функциии полезности

Оценка объектов по многоуровневой системе критериев