Задания по теме «Потенциал поля системы зарядов и заряженной сферы»

7.1. Имеются два электрода в виде концентрических сфер с радиусами a (внутренняя) и b (внешняя). Такая система называется шаровым конденсатором. Найдите потенциал любой точки поля между электродами.

7.2. Вычислите потенциал электрического поля диполя.

7.3. Найдите потенциал поля системы зарядов, находящихся в объеме с линейными размерами l, на расстояниях .

7.4. Изобразите потенциальную диаграмму системы из двух заряженных сфер.

7.5. Вычислите потенциал поля шара радиусом a, равномерно заряженного по объему: а) внутри шара; б) вне шара. Изобразите график , гдеr – расстояние от центра шара. Решите задачу путем интегрирования уравнения Пуассона в сферических координатах, а также используя связь между напряженностью поля и потенциалом.

7.6. По тонкому проволочному кольцу радиуса R равномерно распределен заряд q. Исследовать зависимость потенциала электрического поля на оси кольца от расстояния до его центра. Найти напряженность как градиент потенциала.

7.7. Сфера радиуса , равномерно заряженная зарядом, окружена тонкой концентрической сферой радиуса. Какой заряднадо сообщить внешней сфере, чтобы потенциал внутренней сферы относительно бесконечности обратился в нуль? Зарядтакже равномерно распределен по его поверхности.

Решение задач

7.1. Напряженность E поля между такими электродами выражается формулой

и, следовательно, изменяется в пространстве так же, как и в случае поля точечного заряда, откуда следует, что разность потенциалов между внутренней сферой и какой – либо точкой поля, удаленной на расстояние r от центра конденсатора, равна

.

Разность потенциалов между электродами (сферами) будет равна

.

Из этих двух формул следует

.

Измерив между электродами, можно вычислить потенциал любой точки поля.

7.2. Пусть система зарядов находится в объеме с линейными размерами l. Найдем потенциал поля, создаваемого этой системой зарядов на расстояниях r, больших по сравнению с l. Выберем начало координат O внутри объема, который занимает система зарядов, и определим положение зарядов с помощью радиусов – векторов(на рисунке ___ показан один из радиус – векторовзаряда). Потенциал в точке, определяемой радиус – вектором, равен

.

Так как , то можно положить, что

(символом мы обозначили единичный вектор). Тогда

.

Воспользуемся формулой

при .

Теперь мы можем записать

.

Первый член этого выражения есть потенциал поля точечного заряда величиной . Второй член такого же вида, как выражение, определяющее потенциал поля диполя. Роль электрического момента диполя играет величина

,

которую называют дипольным электрическим моментом системы зарядов.

7.3. Если поле создано несколькими зарядами, то потенциал этого поля равен сумме потенциалов полей, созданных отдельными зарядами

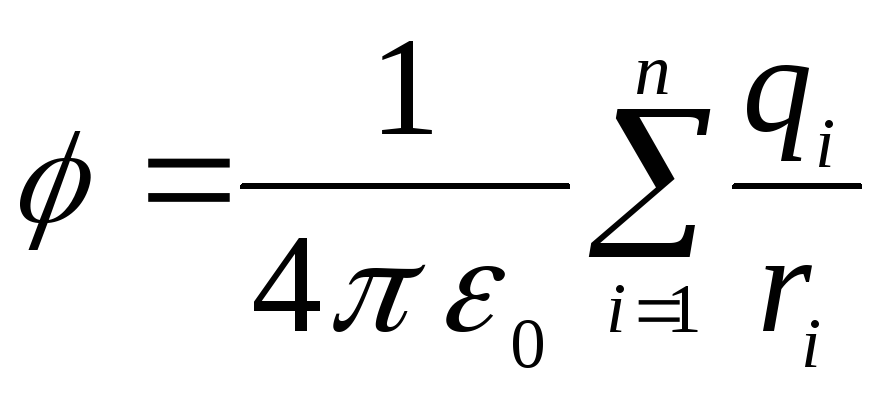
Здесь – потенциал результирующего поля в рассматриваемой точке относительно бесконечности,– расстояние от этой точки дозаряда, а суммирование производится по всем точечным зарядам.

Рассматриваемое поле обладает осевой симметрией, поэтому картина поля в любой плоскости, проходящей через ось диполя, будет одной и той же, а вектор лежит в этой плоскости. Положение точки M относительно диполя будем характеризовать с помощью радиус – вектора, либо с помощью полярных координат r и. Положение зарядаотносительно центра диполя определим вектором, а заряда– вектором. Очевидно, что, где– плечо диполя. Расстояния от зарядовидо выбранной точки M обозначим соответственнои. Так как, то можно положить, что

,

.

Потенциал в точке, определяемой радиус – вектором , равен

.

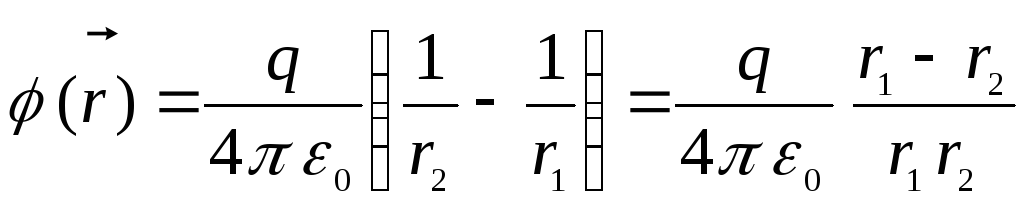Произведение , разность. Следовательно,

,

где – электрический момент диполя.

Из этой формулы видно, что потенциал поля диполя определяется его электрическим моментом. Сравнивая потенциал поля диполя с потенциалом поля точечного заряда, видно, что потенциал поля диполя убывает с расстоянием быстрее , чем потенциал поля точечного заряда.

Из рисунка ___ видно, что . Поэтому

.

7.4. Пусть внутренняя сфера, радиус которой , имеет положительный заряд, а внешняя с радиусом– отрицательный заряд, причем.

Вне сфер потенциал будет равен

,

так как его создают совместно обе сферы (потенциал есть работа внешних сил, совершаемая при перемещении единичного положительного заряда из бесконечности в данную точку поля). Работа по перемещению единичного положительного заряда из бесконечности в область между сферами будет равна сумме двух работ: (работе против сил, действующих со стороны внешней сферы на пути из бесконечности до ее поверхности) и(работе против поля внутренней сферы), т.е.

.

Внутри меньшей сферы потенциал будет постоянен и равен

.

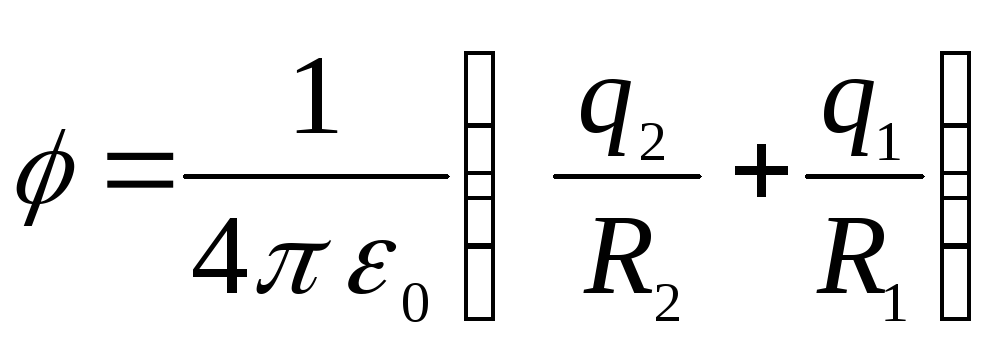График, построенный по первой и второй формулам, изображен на рисунке ____1.

Если заряды сфер будут равны по величине и противоположны по знаку, т.е. (такая система называется сферическим конденсатором), то потенциал во внешней области обращается в нуль, а между обкладками равен

.

Получается график, изображенный на рисунке ___2.

Если внутренняя сфера имеет отрицательный заряд, а внешняя – положительный, то график переворачивается и выглядит так, как изображено на рисунке ____3.

7.5. Интегрирование уравнения Пуассона в сферических координатах. Введем сферическую систему координат ,,, приняв за начало отсчета центр шара. Уравнение Гаусса в дифференциальной форме (уравнение Пуассона), определяющее потенциал поля, принимает вид

,

где .

Вследствие сферически симметричного распределения зарядов, потенциал зависит только от расстояния r и не зависит от углови, т.е.. Поэтому уравнение Пуассона упрощатся и принимает вид

и

.

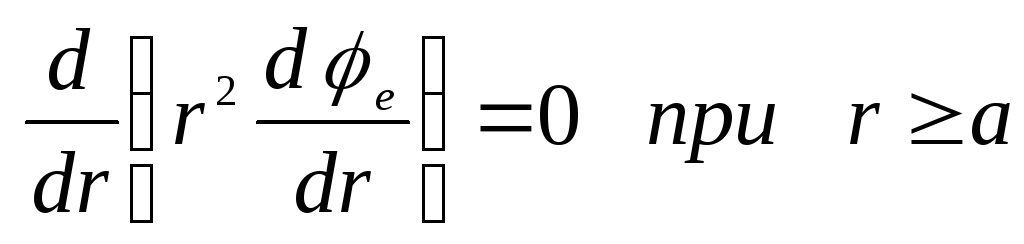Здесь через обозначен потенциал внутри шара, а через– вне шара. Интегрируя эти уравнения, находим

,

.

Постоянные A, B, C, D должны быть определены из следующих граничных условий.

1) Потенциал дожжен оставаться конечным при, откуда непосредственно следует, что.

2) при, откуда следует, что.

3) Потенциал электростатического поля является непрерывной функцией координат, поэтому необходимо, чтобы .

4) Нормальная составляющая вектора не должна испытывать скачка при прохождении через поверхность шара, т.е.при, так как поверхностная плотность заряда на поверхности шара равна нулю. Последнее условие эквивалентно требованию

.

Из последних двух условий находим

,

.

Искомые потенциалы окончательно запишем в виде

,

.

Из этих формул видно, что вне шара потенциал поля аналогичен полю точечного заряда.

Изобразим график .

Пусть ,. Найдем объемную плотность заряда

,

и отношение

.

Теперь можно записать, что потенциал внутри сферы

.

Составим таблицу

	0	0,01	0,015	0,02	0,025	0,03	0,035	0,04
	0

Потенциал вне сферы .

	0,04	0,05	0,06	0,07	0,08	0,09	0,1

Теперь строим график .

Связь между напряженностью и потенциалом.

Зависимость напряженности электростатиического поля от расстояния до центра шара внутри шара имеет вид (см. решение задачи 1.5.4.)

,

т.е. внутри шара напряженность поля растет линейно с расстоянием от центра. При ,, приона достигает максимума и становится равной

.

При напряженность поля зависит от расстояния как напряженность поля точечного заряда.

Изменение потенциала в поле заряженного шара

.

Потенциал поля внутри шара

,

где – потенциал точки на поверхности шара (потенциал поля точечного заряда), равный

.

Окончательно получим

.

Учитывая, что объемная плотность заряда

,

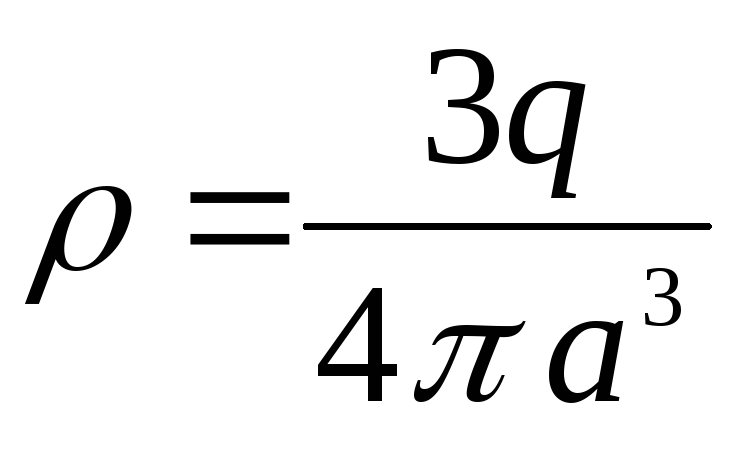можно записать

,

т.е. мы пришли к той же формуле, что и при решении задачи путем интегрирования уравнения Пуассона.

1.7.6. Потенциал результирующего поля в точке A

,

где

есть потенциал поля, созданного зарядом элемента кольца.

есть линейная плотность заряда, r – расстояние от элемента до указанной точки. Из двух последних формул имеем

.

Результирующий потенциал

.

Из геометрических соображений следует, что

.

Следовательно,

.

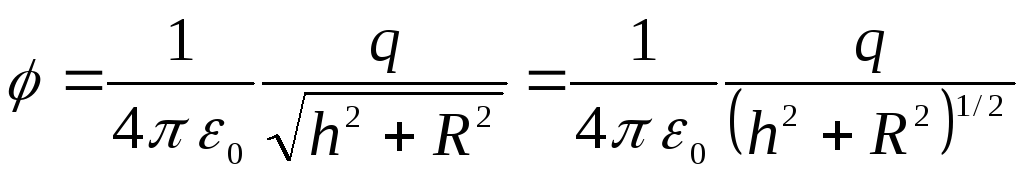Напряженность поля

.

.

Анализ выражений ипоказывает, что в центре кольца () потенциал имеет максимальное значение, а напряженность поля обращается в нуль.

При и потенциал, и напряженность стремятся к нулю.

При производнаяобращается в нуль, следовательно, в этой точке напряженность поля максимальна, а на графике(см. рис. ____) будет точка перегиба. Графикрасположен в 1-й и 3-й четвертях, т.е.,. Это значит, что при переходе через центр кольца () векторменяет свое направление на противоположное.

График расположен в 1-й и 2-й четвертях, т.е. по обе стороны от кольца в точках, лежащих на его оси, потенциал положителен.

На примере решения этой задачи можно убедиться, что при изменении начала отсчета потенциала разность потенциалов между двумя любыми точками не меняется. Не меняется и весь характер зависимости потенциала от расстояния. Например, если выбрать начало отсчета в центре кольца, т.е. если предположить, что , то потенциал любой точки, лежащий на оси кольца, равен

.

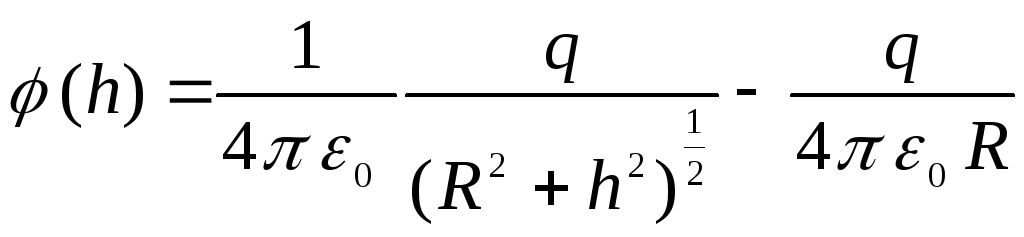Эта формула может быть легко получена на основании принципа суперпозиции.

Если начало отсчета потенциала выбрано в центре кольца, то потенциал поля, созданного элементарным зарядом в точке A, можно представить в виде

.

Интегрируя это выражение по всему кольцу, получим формулу

.

График зависимости , не меняя своего характера, смещается вниз параллельно самому себе на величину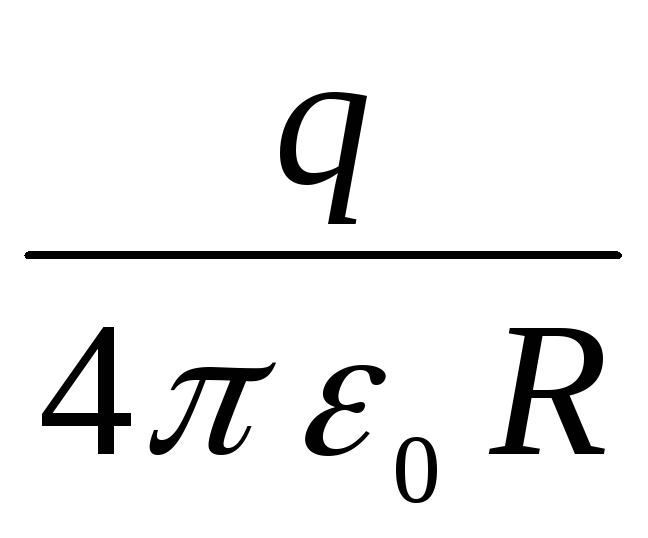(пунктирная линия на рисунке _____2). Припотенциал стремится к значению.

7.7. Потенциал численно равен работе, совершаемой силами электрического поля при перемещении единичного положительного заряда из данной точки поля (в нашем случае, с поверхности внутренней сферы) в бесконечность, т.е.

,

где – результирующая напряженность поля во всех точках интервала интегрирования.

В интервале поле создается только зарядом внутренней сферы. Вектор, независимо от величины и знака заряда, направлен по радиусу от центра. При перемещении единичного положительного заряда отдосилы поля совершают положительную работу. При, т.е. за пределами второй сферы работа сил поля отрицательна и, следовательно, векторнаправлен по радиусу к центру сферы. В точкахполе определяется алгебраической суммой зарядов на обеих сферах. Заряддолжен быть отрицательным и по величине должен быть больше заряда. Так как векторыиколлинеарны (либо антиколлинеарны при), то скалярное произведениеможно заменить произведением(в случае, когда эти два вектора направлены противоположно, напряженность поля должна считаться отрицательной). В формулеподынтегральная функциятерпит разрыв в точке. Поэтому интеграл нужно разбить на два интеграла в пределах отдои отдо:

.

При напряженность

,

а при

.

Подставив эти выражения в соответствующие интегралы, получим

.

Интегрируя и приводя подобные члены, получим

.

Так как по условию задачи , то

.

График зависимости изображен на рисунке ____.

Проанализируем полученный график.

Согласно условию задачи, при заданном значении потенциал на поверхности внутренней сферы. Припотенциал постоянен и равен потенциалу на поверхности, следовательно, графиком на участке отдоявляется прямая линия, совпадающая с осью абсцисс. Привектортерпит разрыв. Так как, то на графике точка(так же, как и точка) представляют особые точки. На участкевекторнаправлен по радиус – вектору. Поэтому, по мере удаления от поверхности внутренней сферы потенциал убывает до некоторого значения. На участкевекторнаправлен навстречу радиус – вектору, поэтому, по мере удаления от поверхности внешней сферы потенциал возрастает, и при. Несмотря на то, что в точкахивектортерпит разрыв, функцияявляется непрерывной.