Національний технічний університет України "КПІ"

Інститут прикладного системного аналізу

Кафедра Системного проектування

Розрахунково-графічна робота

по курсу

“Чисельні методи“

на тему:

"Обчислення визначеного інтегралу методами Боде і Сімпсона та порівняння точності методів"

Виконав: студент гр. ДА-12

Романчук Володимир Ігорович

Перевірив: Корначевський Ярослав Ілліч

Київ – 2012

Зміст

1.Вступ………………………………………………………………………………………………………………………………3

2.Математична частина………………………………………………………………………………………….3

2.1 . Обчислення визначеного інтегралу методом середніх.........3

2.2. Обчислення визначеного інтегралу методом трапецій……….3

2.3.Обчислення визначеного інтегралу методом Сімпсона…….……6

2.4. Обчислення визначеного інтегралу методом Буля………………..7

3.Теоретичний висновок…………………………………………………………………………………………..7

4. Алгоритми………………………………………………………………………………………………………………...9

4.1.Алг. пошуку визначеного інтеграла методом Сімпсона………..9

4.2.Алгоритм пошуку визначеного інтеграла методом Буля…..11

5. Текст програми……………………………………………………………………………………………………..13

6. Тестові приклади………………………………………………………………………………………………….15

7. Висновок……………………………………………………………………………………………………………………19

8. Список використаної літератури…………………………………………………………………19

1.Вступ

Для наближеного обчислення інтеграла функції f(x) використовують методи наближеного інтегрування, найбільш вживані з них базуються на заміні інтеграла скінченною сумою. Для обчислення на проміжку від а(х0) до b(xn), цей проміжок розбивається на n рівних частин, і для точок поділу

x₀ , x₁ , x₂ , x₃ , . . . , x_n-1 , xn

обчислюють значення інтегруючої функції y. Потім потрібно скористуватися формулою наближеного інтегрування.

2.Математична частина

2.1. Обчислення визначеного інтегралу методом середніх.

Це метод прямокутників, у яких на кожному інтервалі за наближення функції береться серединне значення :

.

Сумарна похибка цієї формули буде сума виразів (2) для всіх інтервалів:

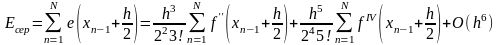
Для будь-якої неперервної функції , знайдеться таке , що .

Тому ; .

Враховуючи, що , маємо остаточно

Похибка методу середніх залежить від квадрату довжини кроку.

2.2. Обчислення визначеного інтегралу методом трапецій.

Формула трапецій

.(1)

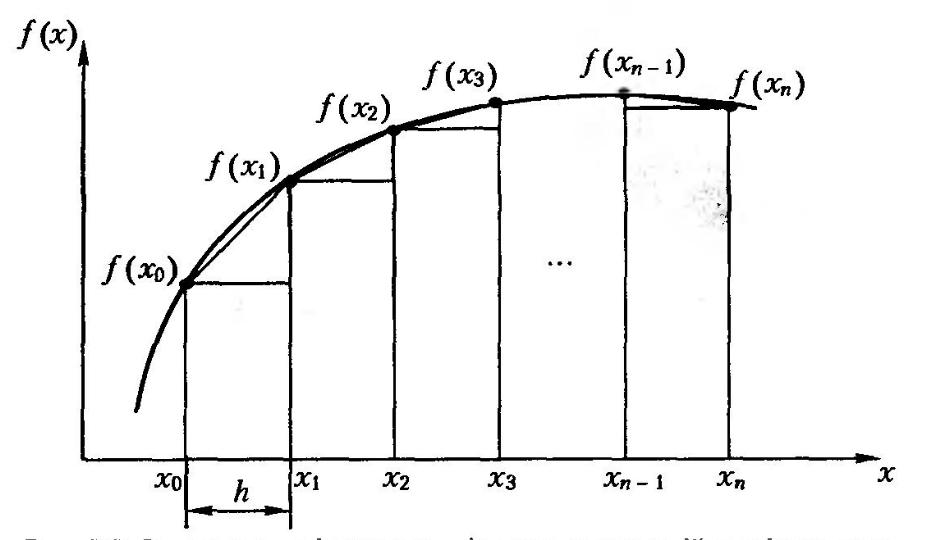
Метод полягає у лінійному наближенні функції на елементарному інтервалі через значення на кінцях інтервалу:

;

;

Тоді

; (1)

; (2)

; (3)

Для більшої зручності при порівнянні методів за точністю виразимо похибки (1) та (3) через значення похідних у серединній точці . Враховуючи, що ; , а також

де (для скорочення), після певних перетворень маємо

.

Таким чином, обидва методи (середніх та трапецій) мають квадратичну точність та при достатньо малому похибка методу середніх вдвічі менша, ніж у методі трапецій та протилежна за знаком.

2.3. Обчислення визначеного інтегралу методом Сімпсона

Формула Cімпсона (парабол)

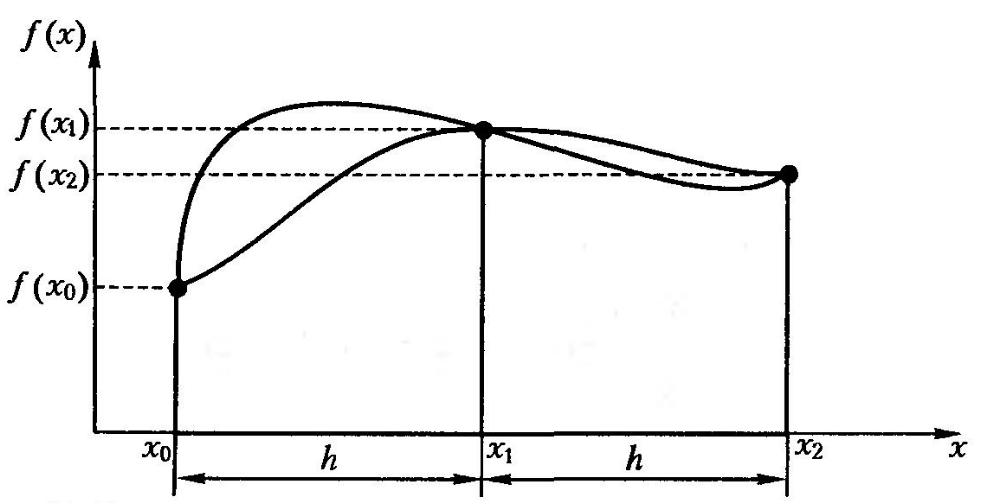
Де n – це кількість розглядуваних точок.

При апроксимації нашого інтегралу замінимо функцію f(x) параболою, що проходить через точки , тобто представимо наближено f(x) в вигляді:

Лагранж запропонував спосіб обчислення таких многочленів:

де базисні поліноми визначаються за формулою:

Очевидно, що мають такі властивості:

при

Звідси випливає, що , як лінійна комбінація , може мати степінь не більший від , та .

Проінтегруємо наш поліном. Вважаючи, що наша задана функція дорівнює інтерполяції Лагранжа, тоді інтеграл заданої функції буде дорівнювати інтегралу полінома.

Проілюструємо вищесказане в пакеті Mathematica 8.0

Таким чином приходимо до наближеної рівності

(3)

Що називається формулою Сімпсона. На цілому відрізку [a,b] формула Сімпсона набуває вигляду:

Перед тим як перходити до оцінки неточностей формули (3) помітимо, що вона являється точною для будь-якого многочлена третьої степені, тобто має місце точна рівність.

Очевидно, що . Цей вираз також наближає обчислюваний інтеграл і дає похибку

2.4. Обчислення визначеного інтегралу методом Буля

Формула Буля (або ще як неправильно його називають метод Боде )

«Boole and Moulton 1960»

По суті формула Буля – це та ж формула Сімпсона, але для інтерполяції 5-го степеня.

Похибка

Також досить відоме правило 3/8 – це інтеграл інтерполяції 4 степеня