
Шпоры со всеми требованиями от Сумина / 16-20
.docx|
16. Математическое ожидание MX дискретной случайной величины. Свойства. Если закон распределения неизвестен, случайную величину изучают по ее числовым характеристикам, одной из которых является математическое ожидание. Опр.1
Математическим ожиданием или средним
значением МX ДСВ X называют MX= Опр.2
Если X
принимает бесконечное, но счетное
множество значений то математическим
ожиданием называется сумма ряда MX= Пример 1 ДСВ Х имеет ряд распределения
Показать, что эта случайная величина не имеет математич. ожидания
|
17. Дисперсия DX дискретной случайной величины. Свойства. Опр.1Дисперсией
DX
ДСВ называется математическим ожиданием
квадратного отклонения случайной
величины X
от ее математического ожидания DX=M Опр.2Если СВ X дискретна с конечными множеством значений то DX= Дисперсия
DX
имеет размерность квадрата случайной
величины, что не всегда удобно. Поэтому
в качестве показателя «разброса»
используется величина
Опр.3Среднеквадратичным
отклонением ДСВ x:
Свойства
дисперсии.
|
18. Функция распределения F(x) случайной величины. Свойства. Для описания закона распределения СВ можно рассматривать вероятности события Х<х Опр.1Функцией распределения СВ Х называется F(x)=P(X<x). F(x) иногда называют интегральной функцией распределения. Замечание 1 Функция распределения любой ДСВ есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины, и равны вероятностям этих значений .Сумма всех скачков функции = 1.
Свойства
F(x)
1).
0≤F(x)≤1
Это следует из того, что функция
распределения это вероятность.2.)Функция
распределения СВ есть неубывающая
функция на всей числовой оси, т.е.
|
||||||||||||
|
19.Непрерывные случайные величины. Плотность распределения вероятностей φ(х) (ее свойства). Опр.1 Случайную величину X называют нерперывной, если множество ее значений бесконечное и несчетное образует числовой промежуток(конечный или бесконечный) Рассмотрим вероятность попадания НСВ на отрезок [x,x+∆x].
P( Делим
обе части на ∆х
и при переходе к пределу ∆х→0,
получим плотность распределения
вероятностей равную
Опр.2
Плотностью распределения называется
производная функции распределения
φ(x)= Замечание 1 Плотность распределения φ(x) является одной из форм закона распределения, существует только для НСВ Свойства плотности распределения.1) φ(x)≥0 Док-во Плотность распределения φ(x)≥0 как производная неубывающей функции распределения F(x)
|
20.Математическое ожидание MX и дисперсия DX непрерывной случайной величины
1)
Математическим ожиданием
НСВ Х, все возможные значения которой
принадлежат отрезку [a,b],
называется определенный интеграл
MX=
2)Дисперсией
НСВ Х , все возможные значения которой
принадлежат отрезку [a,b],
называется определенный интеграл
DX= Замечание Все свойства MX и DX для ДСВ справедливы и для НСВ
|
|
||||||||||||
|
|
18.3
7)
Функция F(x)
непрерывна слева
Тогда
ясно, что
|
|
|
18.1
Док-во
Т.к.
P(
P( 3)F(-∞)=0 F(+∞)=1 Док-во: F(-∞)=P(x<-∞)=0, как вероятность невозможного события x<-∞ F(+∞)=P(x<+∞)=1, как вероятность достоверного события.
4)Вероятность
попадания случайной величины Х в [
P(
|
17.1
2. Постоянный
множитель можно вынести за знак дисп.
возведя его в ^2 D(kX)= Док-во:
Учитывая св-во 2 математического
ожидания, получим
D(kX)=M[kX-M(kX)]2=M(kX-kMX)2=M[k(X-MX)]2= 3.
Дисперсия случ. величины X
может быть записана в виде DX=M Док-во
Пусть
MX=a,
тогда DX=
4 Дисперсия суммы 2-х независимых случайных величин D(X±Y)=DX±DY Док-во: По предыдущему свойству дисперсии D(X±Y)=M D(X±Y)=M |
16.1
Решение
MX= Свойства MX 1) Математическое ожидание постоянной величины равно ей самой Док-во Постоянную величину С=const можно рассматривать как случайную величину, принимающую значение С с p=1.МС=С*1=С 2)
Постоянный множитель можно вынести
за MX.Док-во
Т.к. ДСВ kx
принимает значение
3) Математическое ожидание суммы 2-х случайных величин равно алгебраической сумме мат. ожиданий этих величин. М(X±Y)=MX±MY Док-во:
В соответствии с опред. суммы и разности
случайных величин X
иY
(X-Y)
представляют случайную величину,
которая принимает значения
с
вероятностью
Поэтому
М(X±Y)=
|
|
|
|
19.1
2)
Вероятность попадания НСВ Х на отрезок
[a,b]
равнаP(a≤x≤b)=
Док-во:
P(a≤x≤b)=F(b)-F(a).Т.к.
F(x)-первообразная
для плотности распределения вероятностей
φ(x), то по ф-ле Ньютона-Лейбница имеем
F(b)-F(a)=
Замечание
Геометрически
полученная вероятность равна площади
фигуры, ограниченной сверху кривой
распределения и опирающейся на отрезок
[a,b]
3)Функция
распределения НСВ Х равна F(x)= Док-во Формула получается если подставить пределы в формулу св-ва (2) (a→-∞, если верхний предел b заменить на переменный предел х) 4) Несобственный интеграл 1-го рода от плотности распределения вероятностей НСВ Х равен 1
Док-во:
По
3-му свойству
F(x)= и
при х →+∞ получим F(+∞)=1= |
|
16.24)Математическое
ожидание произведения 2-х независимых
случайных величин M(XY)=MX*MY
Док-во
По
опред. произвед. случ. величины X*Y
представляет собой случайную величину,
которая принимает значение
M(XY)= 5) Математическое ожидание отклонения случ. величины от ее математического ожидания равно нулю. M(X-MX)=0 Док-воM(X-MX)= MX-M(MX), т.к. MX- некоторое число, то по 1 св-ву математич. ожидание M(MX)=MX
|
18.2Док-воПроводя
рассуждения, аналогичные св-ву (2)
P(x< 5)Вероятность того, что НСВ Х примет какое-либо заранее заданное значение равна 0
P(x=
=P( Т.к. Х -НСВ→F(x) непрер-> F(X=X1)=F(X1)-F(X1)=0 6) Вероятности попадания НСВ в интервал, полуинтервал или отр. с одними и теми же концами одна P(a<x<b)=P(a≤x<b)=P(a<x≤b)=P(a≤x≤b) Док-во по св-ву (5)
|
|

 ;
; если этот ряд сходится абсолютно.
Если нет, говорят, что X не имеет MX
если этот ряд сходится абсолютно.
Если нет, говорят, что X не имеет MX





 ;
DX≥0
;
DX≥0


 Дисперсия
постоянной величины=0 Док-во:
Если
C=const,то
DC=
Дисперсия
постоянной величины=0 Док-во:
Если
C=const,то
DC=
 F(
F( F(
F(
 )=F(x+∆x)-
F(
)=F(x+∆x)-
F(

 (x)
(x)
 (замечание
MX=
(замечание
MX= если возможные значения НСВ Х
принадлежат всей числовой оси, при
этом полагается, что насобств. интеграл
1-го рода сходится абсолютно)
если возможные значения НСВ Х
принадлежат всей числовой оси, при
этом полагается, что насобств. интеграл
1-го рода сходится абсолютно) (замечание
DX=
(замечание
DX= -если возможные значения НСВ Х
принадлежат всей числовой оси, при
этом предполагается что данный
несобственный интеграл 1-го рода
сходится)
-если возможные значения НСВ Х
принадлежат всей числовой оси, при
этом предполагается что данный
несобственный интеграл 1-го рода
сходится)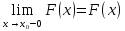 Док-во
выберем
последовательность
Док-во
выберем
последовательность
 сходится к
сходится к
 Обозначим через
Обозначим через
 событиеА={
событиеА={ }
} c
c
 при i>j
и
при i>j
и
 По аксиоме нерперывности
lim(P(
По аксиоме нерперывности
lim(P( =lim(F(
=lim(F( )-F(
)-F( ))=F(
))=F( )-
F(
)-
F( )=0
т.е
)=0
т.е

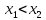 Событие
{X
принимает значения <
Событие
{X
принимает значения < }
можно представить в виде суммы 2-х
событий: {X
принимает значения <
}
можно представить в виде суммы 2-х
событий: {X
принимает значения < }и
{X
принимает значения
}и
{X
принимает значения

 }Вероятность
указанных 2-х событий P(x<
}Вероятность
указанных 2-х событий P(x< )
и P(
)
и P(
 )
. По теореме сложения вероятностей
2-х несовместных событий P(x<
)
. По теореме сложения вероятностей
2-х несовместных событий P(x< )=P(x<
)=P(x< )+P(
)+P(
 )
или P(
)
или P(


 )
≥ 0, то
)
≥ 0, то
 или
или

 )=F(
)=F( )-
F(
)-
F( )≥
0 , откуда F(
)≥
0 , откуда F( )≤F(
)≤F( )
)
 )
равна приращению ее функции распределения
на этом промежутке.
)
равна приращению ее функции распределения
на этом промежутке.
 =
F(
=
F( )-
F(
)-
F(

 M
M =
= DX
DX ;
; M
M =
= -2
-2 +
+ =MX-
=MX- =
= -т.к.
a-
постоянная величина.
-т.к.
a-
постоянная величина. =M(
=M( )-(
)-( ,
обозначая MX=
,
обозначая MX= ,
MY=
,
MY= ,
И учитывая что Y
и X
независимы M(XY)=MX*MY,
запишем
,
И учитывая что Y
и X
независимы M(XY)=MX*MY,
запишем ±2
±2 +M
+M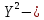 (
( ±2
±2 +
+ )=
M
)=
M ±2
±2 +M
+M ∓2
∓2 -
-
 =
= =
= =∞
→
MX
не существует.
=∞
→
MX
не существует. (i=1..n),то
M(kX)=
(i=1..n),то
M(kX)= =
=
 kMX
kMX
 +
+ (
( -
- (i=
(i= ,
j=
,
j= )
) =
P[(X=
=
P[(X= )(Y=
)(Y= )]
)] =
=
 ±
± =
= ±
± =
MX±MY
=
MX±MY
 =P(a≤x≤b)
=P(a≤x≤b)


 =1
=1 с вероятностями
с вероятностями
 независимы
независимы
 (здесь X=
(здесь X= ),
поэтому
),
поэтому =
= =MX*MY
=MX*MY )=P(x<
)=P(x< )+
P(
)+
P( ≤x<
≤x< ),
откуда P(
),
откуда P( ≤x<
≤x< )=
P(x<
)=
P(x< )-
P(x<
)-
P(x< )=
F(
)=
F( )-
F(
)-
F(
 Док-во
P(
Док-во
P(
 )=
F(
)=
F( )-
F(
)-
F( Пусть
Пусть
 ,
тогда P(
,
тогда P(
 )=
)=
 )=
F(
)=
F( )-
F(
)-
F(