
Шпоры со всеми требованиями от Сумина / 6-10
.docx|
6. Элементы комбинаторики. Размещения, перестановки и сочетания в схемах случайного выбора без возвращения и с возвращением. (ч.1)
Пусть
Если
элемент
Если
элемент
Существует две схемы выбора m элементов из исходного множества
Схема случайного выбора без возвращения:
Число
размещений
Пример
1.
Составить различные размещения из
трех элементов по два элемента множества
D={a,b,c}
и подсчитать их число. Размещения:
(а,b),
(a,c),
(b,c),
(c,a),
(b,a),(c,b).
Ии число равно
|
6.(ч.3) Пример 5. Из 3-х элементов мн-ва D{a,b,c} составить все сочетания по 2 элемента с повторениями и подсчитать их число. Сочетания:
(a,b), (a,c), (b,c), (a,a), (b,b), (c,c). Их
число равно: 6= Число
перестановок
Пример 6. Сколько различных 5-ти значных чисел можно составить из цифр 3,3,5,5,8-? Решение:
здесь n1=2;
n2=2;
n3=1.
n1+n2+n3=5;
следов-но P5(2,2,1)= |
7. Аксиоматическое построение теории вероятностей. Борелевское поле событий, вероятностное пространство. (ч.1) Отправным
пунктом аксиоматики явл-ся непустое
множ-во Ω=Ω( Событием
А{ Будем рассматривать некоторые семейства подмножеств множества Ω. Указанное семейство подмножеств F множества Ω называется борелевским, если 1. В F есть хотя бы один элемент (даже невозможное событие ∅) 2.
Если А∈F,
то
3.
Наряду с конечными или счетными
множествами события
Замечание 1. Отметим, что если Ω=Ω(ω1,…,ωn)-простр-во элемент. событий, то σ-алгебра F содержит все 2n подмножеств {ωl1, ωl2,…,ωl3) ∈Ω Лемма1 Всякое F содержит достоверное событие Ω Док-во По треб. 1 существует хотя
бы один элемент А, по треб.2
Лемма2 Всякое F содержит невозм. событие ∅ Док-во Коль скоро Ω∈F(согласно лемме 1), то невозможное событие ∅=Ω∈F по треб. 2
|
|
7.(ч.3) событий есть невозможное событие,
т.е.
Определение2 Измеримое прост-во (Ω,F ) вместе с опред. на σ-алгебре функцией P(A) удовлетворяющее аксиомам 1-4 называется вероятностным пространством (Ω,F, P) Следствие1 Вероятность невозможное события ∅∈F=0 Док-во: Т.к. Ω=∅∪Ω и ∅∩Ω=∅(несовместные события), то Р(Ω)=Р(∅∪Ω)=Р(∅)+Р(Ω)=1 след-но Р(∅)=0 Следствие2
Для
∀
события А∈F
справедливо: P( Док-во:
Т.к. А∪ Следствие3 Каково бы ни было событие А∈F: 0≤P(A)≤1 Док-во:
Согласно аксиоме 1 Р(А)≥0. Далее
Р(А)+Р( Следствие4 Если событие А∈F влечет за собой событие B∈F, то P(А)≤P(B) Док-во:
Пусть АϲВ.
Запишем В\А= Следствие5 Если события А и В ∈ F, то P(А∪B)=P(А)+P(B)-P(А∩B) Док-во В суммах А∪B=A∪(B\A∩B), B=A∩B∪(B\A∩B) слагаемые явл. Несовместными событиями, поэтому по аксиоме 3 имеем: P(А∪B)=P(A)+P(B\A∩B) P(B)=P(A∩B)+P(B\ A∩B), отсюда, вычитая почленно из 1-го равенства 2-ое, получим: Р(А∪В)- Р(В)= Р(А)-Р(А∩∩В) или Р(А∪В)= Р(А)+Р(В)-Р(А∩В)
|
8.Условная вероятность события. Независимые события (ч.1)
В
ряде случаев приходится рассматривать
вероятность события А при дополнительном
условии, что произошло другое событие
В. Такую вероятность будем называть
условной и обозначать P(A|B)
или
Нетрудно
вывести ф-лу для условной вер-ти в
рамках классич. Теории вер-тей. Пусть
с опытом Ω связаны элементы события
Если
событие В произошло, то наступило одно
из к событий, благопр. В При условии
наступления события В событие А
благоприятств. r событий P(A|B)= Теорема1 Умножение вероятностей. Вероятность произведений 2-х событий равна произведению вероятности одного из них на условную вероятность друго, найденную в предположении, что первое событие уже наступило. Док-во: умножая правую и левую части равенств (1) и (2) соответственно на Р(В) и Р(А), получим: P(AB)=P(A)P(B|A)=P(B)P(A|B) Замечание 1. В случае, если Р(А) или Р(В)=0 соответствующие фор-лы (1) и (2) для условной вер-ти не имеют смысла, ибо события А и В явл. невозможными, однако теор. умножения вер-тей
|
9. Формула полной вероятности. Формулы Байеса. (ч.1) Следствием 2-х основных теорем теории вер-тей - теор. сложения и теор. умножения явл. формула полной вер-ти и фор-лы Байеса. Фор-ла полной вер-ти. Теорема1 Вероятность события А, которое может наступить при условии появления одного из
n
событий(гипотез) Н1,
Н2,…,Нn,
образующих полную группу попарно
несовместных событий равна: P(A)=
Док-во:
Событие А может наступить лишь при
условии наступления одного из
событий(гипотез) Н1,
Н2,…,Нn,
образующих полную группу т.е. А=А P(A)=P( АH1+АH2+..+АHn)=P(АH1 )+P(АH2 )+..+P(АHn )= P(H1 )P(A│H2)+…+ P(Hn )P(A│Hn) Формула
Байеса. Следствием
теоремы умножения и формулы полной
вер-ти явл-ся фор-лы Байеса. Эти фор-лы
применятся,
когда событие А, которое может появиться
с одним из событий (гипотез)
Для
получения искомой формулы запишем
теорему
умножения вероятностей событий А и
Нi(i=1,…n)
в 2-х формах: P(A P(
|
|
10. Теорема Бернулли. (ч.1) Теорема1
Если вероятность Р наступления события
А в каждом испытании постоянна, то
вероятность Pn(m)
того, что событие А наступит m раз в n
независимых испытаниях равна Pn
(m)= Док-во
Пусть события
i=1..n;
соб. Bm={в
n независимых испытаниях событие А
происходит m раз} Представим событие
Bm
через соб. Аi
(i=1,…,n)(элементарные
события в схеме Бернулли). Например
при n=3 m=2 событие B2
можно записать в следующем виде: :
В общем случае событие В запишется так:
Число
всех комбинаций(слагаемых суммы (2))
равно числу сочетаний
В
связи с тем, что указанные комбинации
между собой несовместны, по теореме
сложения вероятностей получим:
Пример 1. Вероятность изготовления на автоматическом станке стандартной детали равна 0,8. Найти вероятность появления возможного числа бракованных деталей (m=0,1,2,3,4,5) среди 5-ти отобранных деталей. Решение: искомые вер-ти находим по фор-ле Бернулли: |
|
|
|
7.(ч.2) Определение1 Мн-во Ω вместе с выдел. в нем борелевским полем событий F назыв. измеримым пр-м. Будем обозначать ( Ω, F) Замечание 2. Отметим, что если Ω-конечное множ-во, то совокупность всех подмножеств Ω, включая и пустое множ-во ∅ и само множ-во Ω, образует Борелевское поле событий F. Пример
1. Бросание
игральной кости. Множ-во
элемент. событий состоит из 6-ти элем.
ω1,
ω2,…,
ω6,
где событие ωi(i= Аксиомы, опред. вероятность. А1 Каждому событию А∈F ставится в соотв. неотрицательное число P(А), назыв. вероятностью (т.е. P(А)>0) А2 Вероятность достоверного события Ω принадлеж. F равна 1 А3
Если конечное или счетное множество
событий
P( А4
Если последовательность событий А1,…,
|
|
6.(ч.2) Общее
число перестановок
Pn
из
n
элементов равно: Pn=Ann= Пример 2. Составить различные перестановки из 3-х элементов мн-ва D={a,b,c} и посчитать их число. Перестановки: (а,b,с), (а,с,b), (b,a,c), (b,c,a), (c,a,b), (c,b,a). Их число равно: 6-Р3=3!=6.
Число
сочетаний
Пример 3. Сост. различные сочетания из 3-х элем. по 2 элем. мн-ва D{a,b,c} и посчитать их число.
Сочетания:
(a,b), (b,c), (c,a). Их
число равно: 3=
Отметим
разницу между размещениями
Схема случайного выбора с возвращением:
Число
размещений
Пример 4. Из 3-х элементов множ-ва D={a,b,c} составить все размещения по 2 элемента с повторениями и подсчитать их число. Решение:
Размещения
(a,b),
(a,c),
(b,c),
(b,a),
(c,a),
(c,b),(c,c),
(b,b),
(a,a):
их число равно:
Число
сочетаний
|
|
9. (ч.2) Полученные формулы наз-ся формулами Байеса. Замечание 1. Значение фор-лы Байеса состоит в том, что при появлении события А, т.е. по мере поступления новой информации можно проверять и корректировать выдвинутые до испытания гипотезы, основываясь на переходе от их априорных вер-тей к апостериорным (рис.1) |
8.(ч.2) остается справедливой и при Р(А)=0 Следствие 1. Теорема умножения вер-тей обобщается на случай произвольного числа событий:
P( Определ. 1. Событие А называется независимым от события В, если его вер-ть не меняется от того, произошло событие В или нет, т.е. Р(А│В)=Р(А). В противном случае, если Р(А│В)≠Р(А), событие А называется зависимым от события В. Теорема2 Если событие А не зависит от события В, то и соб. В не зависит от соб. А Док-во Т.к. А не зав. от В то P(A|B)=P(A) Запишем теорему умнож. вер-тей в двух формах: P(AB)=P(A)P(B|A)=P(B)P(A|B).Заменяя Р(А│В) на Р(А), получаем P(A)P(B|A)=P(B)P(A) или P(B|A)=P(B), т.е. соб. В не зависит от соб. А. Т.о., завис-ть и независ-ть событий всегда возможна
Определение2
Независимые
события
Пример 1. 3 события А,В и С независимы в совокуп., если независимы события А и В, В и С, А и С, А и ВС, В и АС, С и АВ Замечание 2. Для независ. событий теор. умнож. вер-тей для 2-х и нескольких событий принимает вид: Р(АВ)=Р(А)*Р(В) Р(А1,А2,…,Аn)=Р(А1)*Р(А2)…Р(Аn) |
|
|
|
|
10. (ч.2) На рис. видно, что что существует значение m=m0=1, при котором Рn(m) принимает значение max. Это значение m0 наз-ся наивероятнейшим. Многоугольник – распределение вер-тей. Для нахождения m0 запишем систему неравенств: Pn(m0)≥ Pn(m0+1) Pn(m0) ≥Pn(m0-1) Решим
1-ое нер-во системы, используя формулу
Бернулли и фор-лу числа сочетаний
(n-
m0)!=
(n-
m0-1)!
(n-
m0),
то получаем нер-во:
Замечание 2. Отметим, что разность np+q-(np-q)=p+q=1, то всегда существует хотя бы одно целое значение m0, удовлетворяющее неравенству (4). Пример 2. Сколько раз необходимо подбросить игр. кость, чтобы наивероятнейшее выпадение тройки было равно 10? Решение: В данном случае p=1/6, q=1-p=5/6, m0=10. Согласно нер-ву (4), можно записать: n*1/6-5/6 ≤ 10 ≤ n*1/6+1/6 или n-5 ≤ 60 ≤ n+1 n-5 ≤ 60 59 ≤ n ≤ 65 n+1 ≥ 60 т.е. необходимо подбросить игр. кость от 59 до 65 раз включительно.
|

 ,
i=1,k
элементы некоторого конечного множества
,
i=1,k
элементы некоторого конечного множества можнет быть выбрать
можнет быть выбрать
 способоми, элемент
способоми, элемент
 можно выбрать другими
можно выбрать другими
 способами, и т.д
способами, и т.д
 способами, отличными от первых (k-1),
то выбор одного из элементов или
способами, отличными от первых (k-1),
то выбор одного из элементов или
 ,…,
или
,…,
или
 может быть осуществлен
может быть осуществлен
 способами.
способами. можно выбрать
можно выбрать
 способами, после такого выбора элемент
способами, после такого выбора элемент
 может быть выбран
может быть выбран
 способами,…,
после каждого (k-1)
выбора элемент
способами,…,
после каждого (k-1)
выбора элемент
 может быть выбран
может быть выбран
 способами, то выбор всех элементов
способами, то выбор всех элементов
 в указанном периоде может быть
осуществлен
в указанном периоде может быть
осуществлен
 способами.
способами. из n элементов по m элементам равно:
из n элементов по m элементам равно: =
=

 =
= =
= =
= =6.
=6. из n
элементов с повторением:
из n
элементов с повторением:
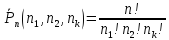 где
n=
где
n=
 3*2*5=30
3*2*5=30 ),
называемое простр-вом элементарных
событий, а его элементы ω1,…,
),
называемое простр-вом элементарных
событий, а его элементы ω1,…,
 - элементарными событиями.
- элементарными событиями.
 }
тогда назовем любое подмножество
множества Ω
}
тогда назовем любое подмножество
множества Ω

 ∈
F,
борелевскому полю F принадл. всевозможные
суммы
∈
F,
борелевскому полю F принадл. всевозможные
суммы
 и произведения
и произведения

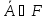 ,
тогда событие Ω=
А∪
,
тогда событие Ω=
А∪ ∈F
по треб. 3
∈F
по треб. 3
 )=1-P(A)
)=1-P(A) =Ω
и А∩
=Ω
и А∩ =∅,
то Р(Ω)=Р(А∪
=∅,
то Р(Ω)=Р(А∪ )=Р(А)+Р(
)=Р(А)+Р( )=1
след-но Р(
)=1
след-но Р( )=1-Р(А)
)=1-Р(А) )=1,
но Р(
)=1,
но Р( )≥0
след-но 1-Р(А)≥0, т.е. Р(А)≤1
)≥0
след-но 1-Р(А)≥0, т.е. Р(А)≤1 ∩В
(рис.1). Очевидно, что В=(В\А)∪А,
т.к. события В\А и А несовместные,то
Р(В)=Р((В\А)∪А)=Р(В\А)+Р(А),
т.к. Р(В\А)≥0, то Р(В)-Р(А)≥0, т.е. Р(А)≤Р(В)
∩В
(рис.1). Очевидно, что В=(В\А)∪А,
т.к. события В\А и А несовместные,то
Р(В)=Р((В\А)∪А)=Р(В\А)+Р(А),
т.к. Р(В\А)≥0, то Р(В)-Р(А)≥0, т.е. Р(А)≤Р(В) .
Это означает вер-ть события А при
условии, что событие В уже произошло.
.
Это означает вер-ть события А при
условии, что событие В уже произошло.
 Пусть событие А благопр. m событиям из
этой группы, событие В (не являющ-ся
невозм) благопр. к событиям. Событие
А∩В=АВ благоприятствует r событий
(r≤m,
r≤k)
Пусть событие А благопр. m событиям из
этой группы, событие В (не являющ-ся
невозм) благопр. к событиям. Событие
А∩В=АВ благоприятствует r событий
(r≤m,
r≤k) (1). Точно также если событие А не явл.
невозможным, получаем: P(B|A)=
(1). Точно также если событие А не явл.
невозможным, получаем: P(B|A)= (2)
(2)
 причем ввиду несовместности соб.
Н1,…,Нn,
события Н1А,
Н2А,…,
НnА
также несовместны, поэтому на основании
теорем слож. и умн. Вер-тей можно
записать
причем ввиду несовместности соб.
Н1,…,Нn,
события Н1А,
Н2А,…,
НnА
также несовместны, поэтому на основании
теорем слож. и умн. Вер-тей можно
записать
 ,…,Нn
, произошло и необходимо произвести
конечную переоценку априорных (до
опыта) вероятностей P(
,…,Нn
, произошло и необходимо произвести
конечную переоценку априорных (до
опыта) вероятностей P( ),
P(
),
P( ),…,
P(
),…,
P( ),
т.е. необходимо найти апостериорные
(после опыта) условные вероятности
P(
),
т.е. необходимо найти апостериорные
(после опыта) условные вероятности
P( |А),
P(
|А),
P( |А),…,
P(
|А),…,
P( |А).
|А). )=P(A)P(
)=P(A)P( ,
откуда
,
откуда
 q=1-p
(1)
q=1-p
(1) и
и
 {появление
или непоявление события А в i-ом
испытании}
{появление
или непоявление события А в i-ом
испытании} =
= .
. ..
.. (2)
(2) .
Вероятность каждой такой комбинации
по теореме умножения вероятностей
равна
.
Вероятность каждой такой комбинации
по теореме умножения вероятностей
равна
 P(
P( ,
P(
,
P( )=1-p,
i=1,…,n
)=1-p,
i=1,…,n
 )
означает выпадение i
очков.
Борелевское поле событий состоит из
26=64
(1+
)
означает выпадение i
очков.
Борелевское поле событий состоит из
26=64
(1+ =7+15+90+15+6+1=64)
элементов: ∅, {ω1},
{ω2},…,
{ω1ω2},…,
{ ω5ω6},
{ω1ω2ω3},…,{
ω1ω2
ω3ω4
ω5ω6}=Ω
=7+15+90+15+6+1=64)
элементов: ∅, {ω1},
{ω2},…,
{ω1ω2},…,
{ ω5ω6},
{ω1ω2ω3},…,{
ω1ω2
ω3ω4
ω5ω6}=Ω ∈F
попарно несовм. то
∈F
попарно несовм. то
 )=P(
)=P(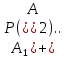
 ∈F
такова, что каждое последующее влечет
за собой предыдущее, т.е
∈F
такова, что каждое последующее влечет
за собой предыдущее, т.е
 Ɔ
Ɔ Ɔ…
Ɔ… и произведение всех
и произведение всех
 =n!
=n! из n элементов по m элементам:
из n элементов по m элементам:
 =
= =
=
 =
= =
= =3
=3 и сочетаниями
и сочетаниями
 :
в размещениях учитывается порядок
следования элементов, в сочетаниях-нет.
:
в размещениях учитывается порядок
следования элементов, в сочетаниях-нет. из n
элементов по m
элементам с повторением:
из n
элементов по m
элементам с повторением:


 из n элементов по m элементам c
повторением:
из n элементов по m элементам c
повторением:
 =
=
 )=P(
)=P( )P(
)P( )P(
)P( )..P(
)..P( )
) назыв. независимыми в совокупности,
если независимы любые 2 из них и
независимы любое из данных событий и
любые комбинации(произведения)
остальных событий.
назыв. независимыми в совокупности,
если независимы любые 2 из них и
независимы любое из данных событий и
любые комбинации(произведения)
остальных событий. .
Запишем
.
Запишем .
Т.к. (m0+1)!=
m0!(m0+1),
.
Т.к. (m0+1)!=
m0!(m0+1), q≥
q≥ p,
или (m0+1)q≥(n-m0)p,
откуда m0≥np-q
(т.к. p+q=1).
Решая аналогично 2-е нер-во, получим,
что m0≤np+p.
Получим окончательно: np-q≤m0≤np+p
(4)
p,
или (m0+1)q≥(n-m0)p,
откуда m0≥np-q
(т.к. p+q=1).
Решая аналогично 2-е нер-во, получим,
что m0≤np+p.
Получим окончательно: np-q≤m0≤np+p
(4)