
Шпоры со всеми требованиями от Сумина / 11-15
.docx|
11.Теорема
Пуассона
Если
вероятность p настпления события А в
каждом исытании →0 при n→∞, причем
pn→λ,
то вероятность
Док-во
Функция Бернули
Учитывая,
что предел
|
12.
Локальная теорема Муавра-Лапласа
Если вероятность наступления некоторого
события А в n независмых испытаниях
постоянна и равна p(0<p<1),
то вероятность
m=
Рассмотрим теперь:
=
- (np+ -(nq- по
условию
|
13.(1)
Интегральная теорема Муавра-Лапласа
Если m
есть число наступления события А в n
независимых испытаниях, в каждом из
которых вероятность этого события
равна p(0≤P≤1),
то равномерно относительно а и b
(-∞≤a<b≤+∞) при n→∞
имеет место соотношение
Док-во
Будем доказывать частный случай, когда
а и b конечны. Введем для кратности
обознач
у= Вероятность
|
||||
|
14.Полиномиальная схема Как отмечалось выше, схема Бернули представляет n независимых испытаний с 2-мя исходами. При этом в каждом испытании событие А может появиться с одной и той же вер-тью р, а событие Ā с вер-тью q=1-p. В полиномиальной схеме осуществляется переход от n-ти независимых испытаний с 2-мя исходами (А и Ā) к n-ти независимых испытаний с к (к>2) исключающих друг друга испытаний А1….Аn. При этом в n независимых испытаниях событие А1, А2,...Аk наступает m1, m2, …, mk раз с вероятностями p1, p2,…,pk (m1+ +m2+ …+ mk=n). Тогда можно записать, что:
Формула
получается с учетом того, что события
состояли в появлении в n незав. испытаниях
события
А число несовместных вариантов определено числом перестановок с повторением из n элементов.
|
15.Закон распределения дискретной случайной величины (ряд распределения) Под случайной величиной понимается переменная величина, которая в зависимости от исхода испытания случайно принимает одно значение из множества возможных значений. Какое именно – заранее неизвестно Примеры 1) Число очков выпавших при однократном бросании игральной кости есть случ. величина, которая может принимать одно из значений: 1, 2, 3, 4, 5, 6 2)Кол-во бракованных изделий в данной партии. 3) Число произведенных выстелов до 1-ого попадания в цель. 4) Дальность полета артиллерийского снаряда. Определение 1 Случайная величина называется дискретной, если множество ее значений конечное или бесконечное, но счетное. Определение 2 Случайная величина называется непрерывной величиной, если бесконечное счетное множество ее значений образует числовой промежуток (конечный или бесконечный). Случайные величины обычно обозначаются буквами X, Y, Z,….,а их значения соответствующими строчными буквами x, y, z. Определение 3 Случайной величиной назовем вещественно значащую ф-ию X=f(ω), определенную на вероятностном пр-ве (Ω, F, P) и измеримую относительно борелевсого поля событий F Определение 4 Подсуммой(произведением) случайных величин X и Y, понимают случ. величину Z=X+Y (Z=X*Y), возможные значения которых состоят из сумм (произведений) каждого возможного значения случ. величины X и каждого возможного значения случайной величины Y. |
13(3).
Т.к.
| Замечание 1 Простым следствием соотношения Pn(a,b)= Аналогично локальной ф-ле М-Л приближенные значения вер-тей, даваемые интегральной ф-лой (2) на практике использ-ся как точные, если npq≥20 Замечание
2 Выражение
Ф(х)= что а) ф-ция Ф(х)-нечетная т.е. Ф(-х)=Ф(х) б)при х→∞ Ф(х)→0,5 (при |x|≥5 можно считать, Что
Ф(х)= Следствие 1 С помощью интегральной формулы Муавра-Лапласа можно найти вер-ть отношения относит. частоты nA/n соб. А от вер-ти р в n независимых испытаниях. Имеет место Pn
(|nA/n
– p|<ε)≈2Ф(ε |
||||
|
|
|
|
||||
|
13(2). единственная
точка
Т.к
мах значение вероятности
⇒| Действительно,
при таком m
в полуинтервале
≤|x||x- |
12. ⇒Разложим ln в ряд маклорена ln(1+ ln(1- Нетрудно
получить что
Далее,
Замечание 1 Чем больше n, тем точнее приближенная (3), называемая локальной ф-лой Муавра-Лапласа. Приближенные значения вер-ти, даваемые ф-лой (3) на приктике используются как точные, если npq≥20
Замечание
2
Выражение φ(x)= При посторении графика y= φ (x) необходимо учитывать, что 1) φ(-x)= φ(x) (при |x|≥4 можно считать, что φ(x)=0) |
11.
Замечание
Если p
– cosnt
и мала, число n
велико, а число np=λ,
незначительно (np≤10), то из пред.
равенства следует формула
|
||||
|
13.4 Док-во Из нер-ва |nA/n – p|<εследует, что ε≤nA/n – p≤ε, np-nε≤nA≤np+nε По формуле (2) получаем, Pn(np-nε≤nA≤np+nε)≈
Пример 1 Вер-ть попадания в цель при одном выстреле равна 0,6. Найти вер-ть того, что при n=1200 независимых выстрелах, отклонение «частоты» от вер-ти по модулю не превышает ε=0,05 Решение
P1200(|nA/n-0,6|≤0,05)≈2Ф(0,05 =2Ф(3,54)=0, 9996 |
15. Определение 5 Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Для ДСВ закон распределения может быть задан в виде таблицы, аналитически, графически. Простейшей формой записи закона распределения ДСВ Х является таблица:
Такая таблица (матрица) называется рядом распределения дискретной случ. величины Х. Отметим, что событие X=x1, X=x2,…, X=xn образуют полную группу попарно несовместных событий, поэтому
Ряд распределения может быть изображен графически. Полученная ломанная называется многоугольником или полигоном распределения вероятностей |
14. Замечание 1 Частный случай 2-х исходов при m1=m, m2=n-m, p1=p, p2=q=1-p полиномиальная формула (1) переходит в формулу Бернули. |
||||
|
|
|
|

 того, что в n
независимых испытаний событие А
наступит m
раз, определяет предельное равенство
того, что в n
независимых испытаний событие А
наступит m
раз, определяет предельное равенство


 {
{ }
, запишем:
}
, запишем: =
=

 ,
того, что в этих испытаниях событие А
наступит ровно m раз, удовлетворяет
при n→∞ соотношению
,
того, что в этих испытаниях событие А
наступит ровно m раз, удовлетворяет
при n→∞ соотношению Равномерно
для всех m
таких, что x=
Равномерно
для всех m
таких, что x= наход-ся на конечном отрезке Док-во
По
формуле Стирлинга при k→∞; k!=
наход-ся на конечном отрезке Док-во
По
формуле Стирлинга при k→∞; k!= ,
|
,
| |≤
|≤
 +np→n-m=nq-
+np→n-m=nq- Если
Если
 прин. конечному отрезку, то числа m и
(n-m)→∞
вместе с n→∞.
Поэтому применим формулу Стирлинга
прин. конечному отрезку, то числа m и
(n-m)→∞
вместе с n→∞.
Поэтому применим формулу Стирлинга
 =
= <
< Видно,
что каков бы не был отрезок а≤
Видно,
что каков бы не был отрезок а≤ ≤b,
величина
≤b,
величина
 равномерно →0 относительно m и n при
n→∞ ⇒
равномерно →0 относительно m и n при
n→∞ ⇒
 ;
ln
;
ln ]=
]= )ln(1+
)ln(1+ );
);
 )ln(1-
)ln(1- )
)

 ⇉
⇉
 Эта вероятность равна
Эта вероятность равна
 распространенной на те значения m
для которых а≤
распространенной на те значения m
для которых а≤ ,
,
 Опред.
Ф-ю у=
Опред.
Ф-ю у= след. образом:
след. образом: =
=
 у=
у= и прямыми x=
и прямыми x= и x=
и x= т.е
т.е
 Отметим на Ох точки а и b
при n→∞
на [a, a+
Отметим на Ох точки а и b
при n→∞
на [a, a+ ]
найдется единственная точка
]
найдется единственная точка
 на
[b,
b+
на
[b,
b+ ]
]
 (1)
(1) -
-
 раз, А2
-
m2
раз, …
раз, А2
-
m2
раз, …
 -
- раз.
Можно представить в виде суммы
несовместных вариантов вероятность
каждой из которых по теореме умножения
для независимых событий=
раз.
Можно представить в виде суммы
несовместных вариантов вероятность
каждой из которых по теореме умножения
для независимых событий=


 |≤max|
|≤max| |
| +
+
 ≈
Ф(b)-Ф(a)
является соотношением Pn(m1≤m≤m2)≈Ф(х2)-Ф(х1)
(2), где Ф(х)=
≈
Ф(b)-Ф(a)
является соотношением Pn(m1≤m≤m2)≈Ф(х2)-Ф(х1)
(2), где Ф(х)= ,
x1=
,
x1= ,
x2=
,
x2=
 наз-ся нормированной
ф-ей Лапласа.
При построении ее графика (рис) следует
учитывать,
наз-ся нормированной
ф-ей Лапласа.
При построении ее графика (рис) следует
учитывать, 0,5)
0,5) )
) такие, что
такие, что
 =
=
 приходится на значение
приходится на значение
 цел. часть, то макс. знач
цел. часть, то макс. знач
 приходится на интервал 0≤
приходится на интервал 0≤ ≤x<
≤x< для которого справедлива локальная
теорема Муавра –Лапласа, поэтому при
n→∞
max
Пn(x)=Пn(x0)<
для которого справедлива локальная
теорема Муавра –Лапласа, поэтому при
n→∞
max
Пn(x)=Пn(x0)<
 |=|
|=| |≤
|≤ <
< Т.к числа а и b
–конечные, то согласно локальной
теореме Муавра-Лапласа при а
Т.к числа а и b
–конечные, то согласно локальной
теореме Муавра-Лапласа при а
 [1+
[1+ (
( )]
где
)]
где
 (
( ⇉0
относительно
⇉0
относительно
 при n→∞ При промежуточном значении
x
при n→∞ При промежуточном значении
x
 [1+
[1+ (
( )]
причем
)]
причем
 =0
=0 имеем
имеем
 [1+
[1+ (
( )]
где
)]
где
 (
( [1+
[1+ (
( )]-1
Т.к
)]-1
Т.к

 |<
|<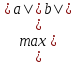 ,
то ясно, что
,
то ясно, что
 =0
=0
 =
=
 =
= 0͇
0͇ ;
; ⇉1
(n→∞) на
[a,b]
⇉1
(n→∞) на
[a,b] а≤
а≤ ≤b;
≤b;
 ;
; ⇉1
или
⇉1
или
 (3)
(3) называется формулой Гауса, а ее график
–кривой вероятностей. (рис)
называется формулой Гауса, а ее график
–кривой вероятностей. (рис) ..=
..=

 =
=



 =
=
 =
2Ф(ε
=
2Ф(ε )
)
 )=
)= (сокращенно
X=
(сокращенно
X= ),
i=1,…n)
),
i=1,…n) =
=