
Шпоры со всеми требованиями от Сумина / 32-37
.docx|
32 Зависимость и независимость двух случайных величин Зная законы распределения СВ X и Y входящих в двумерное СВ, законы распределения можно найти только тогда, когда СВ незавимы. Определение СВ X и Y независимы, если незав. является событие (X<x) и (Y<y) для ∀ действ. чисел x и y, иначе назыв. зависимыми. Теорема1
СВ X
и Y независмы тогда и только тогда,
когда функция распределения F(x,y)= Док-во:
Необходимость.
Пусть СВ X
и Y
независимы, тогда события (X<x) и (Y<y)
независимы. Поэтому Р[(X<x)(Y<y)]=Р(X<x)*Р(Y<y),
т.е. F(x,y)= Достаточность.
Пусть F(x,y)= Замечание1. Заметим. Что равенство (1) есть иначе записанное условие независимости 2-х событий (P(AB)=P(A)P(B) где A=(X<x), B=(Y<y)) Теорема2
НСВ
X и Y независимы тогда и только тогда,
когда φ(x,y)= |
33 Математическое ожидание и дисперсия двумерной случайной величины (дискретной и непрерывной). Определение1:
МО ДСВ (X,Y)
называется совокупность 2-х математических
ожиданий MX
и MY
, определяемых равенством MX= Определение2:
Дисперсия
ДСВ (X,Y)
называется совокупностью 2-х дисперсий
DX
и DY
определяемых равенством: DX=
|
34. Корреляционный момент (ковариация) и коэффициент корреляции. Их свойства (без доказательства). Корреляционным
моментом или ковариацией
2-х СВ X
и Y
называется Kxy=cov(X,Y)=M[(X-MX)(Y-MY)]= Свойства ковариации: 1)ковариация симметрична, т.е. Kxy= Kxх Док-во: следует из определения ковариации. 2)дисперсия СВ есть ковариация её с самой собой, т.е. Kxх=DX, Kxy=DY Док-во: Запишем Kxх< M[(X-MX)(X-MX)]= M(X-MX)2=DX аналогично Кyy=DY 3)Если СВ X и Y независимы, то Kxy=0 Док-во: Из независимости СВ X и Y следует независимость их отношений (X-MX) и (Y-MY) Пользуясь свойствами МО, запишем Kxy= M[(X-MX)(Y-MY)]=M(X-MX)M(Y-MY)=0*0=0
|
|
35 Неравенства Маркова и Чебышева 1)Теорема1.
Неравенство
Маркова:
Если СВХ принимает только неотрицательные
значения и имеет математическое
ожидание, то для любого положительного
числа P(x≥ε)≤ Док-во:
Док-во проведем для непрерывной СВ Х
с плотностью распределения вероятностей
φ(х). Запишем P(x≥ε)= Замечание:
отметим, что неравенство (1) можно
записать в другой форме P(x<ε)≥1- 2)
Теорема2.(
Неравенство
Чебышева)
Для любой СВ Х, имеющей MХ
и DX
справедливо P(|x-MX|≥ε)≤ Док-во: док-во проведем для НСВ Х с плотностью распределения вероятностей φ(х). Обозначим МХ=а. Вероятность P(|x-MX|≥ε есть вероятность попадания СВ Х в область, лежащую вне отрезка [а- ε,а+ ε].
|
36. Закон больших чисел. Теорема Чебышева. Теорема Бернулли (без доказательства) Определение
СВ
Теорема
1.( Закон больших чисел в форме Чебышева)
Если СВ
Док-во:
т.к.
D
|
3 7 Центральная предельная теорема (без доказательства) Теорема ЦПТ Пусть
СВ
P( Замечание. Отметим, что
Замечание следствием ЦПТ являются рассмотренные ранее локальная и интегральная теоремы Муавра-Лапласа. |
|
34.(3)Замечание: Из свойства 3 следует, что если Kxy≠0, то СВ X и Yзависимы. В этом случае СВ X и Y называют корремированными. Однако из того, что Kxy=0, вообще говоря, не следует независимость СВ X и Y. В этом случае (Kxy=0) СВ X и Y называют некорремированными.
Для
DX
и DY
является частными случаями центр.
момента пор
DX=M Определение
Коэффицент корреляции
Отметим, что коэффициент корреляции является лучшей оценкой степени влияния одной СВ на другую по сравнению с ковариацией.
|
|
|
|
34(2)4)D(X Док-во:
Запишем
D(X Аналогично, D(X-Y)=D[X+(-Y)]=DX-2 Kxy+DY 5)Постоянный множитель можно вынести за знак ковариации, т.е. Кcx,y=cКxy=Кx,cy или cov(cX,Y)=c*cov(X,Y)=cov(X,cY) Док-во: Запишем Кcx,y=M[(cX-M(cX))(Y-MY)]=M[c(X-MX)(Y-MY)]=cM[(X-MX)(Y-MY)]=cKx,y 6)Ковариация не изменится, если к одной из СВ или к обоим сразу прибавить постоянную, т.е. Kx+c,y=Kx,y+c=Kx+c,y+c или cov(X+c,Y)=cov(X,Y+c)=cov(X+c,Yc)=cov(X,Y) Без док-ва. 7) Ковариация 2-х СВ X и Y по абсолютной величине не превосходит произведения их средних квадратических отношений, т.е.∣Kxy∣≤σxσy Без док-ва.
|
33.Отметим, что МО MX и MY являются частными случаями начального момента υks порядка k+s двумерной СВ (X,Y) , определяемого равенством υks=M(XkYs) Отсюда MX=M(X1X0)=υ1,0 , MY=M(X0Y1) = υ1,0 Дисперсия DX и DY являются частными случаями центрального момента µks порядка k+s ДСВ (X,Y) определяемого равенством µks=M[(X-MX)k(Y-MY)s] Отсюда DX=M(X-MX)2= µ2,0 DY=M(Y-MY)2= µ0,2 |
32.Док-во:
Необходимость.
Пустть НСВ X и Y независимы, тогда
справедливо равенство (1). Дифференцируем
это неравенство сначала по х, потом
по у, получим Достаточность.
Пусть φ(x,y)=
Теорема3
ДСВ
независима тогда и только тогда, когда
P([(X=
|
|
|
36.Следствие
1
Если СВ X1,X2…Xn
независимы и одинаково распределены,
т.е.
Док-во:
Т.к.
Т.
Бернулли
Если вероятность появления события
А в каждом испытания равна p, число
наступ. этого события при n. независимых
испытаниях равно
|
35.Можно
записать P(|x-а|≥ε)= Имеем
P(|x-а|≥ε)≤1/
ε2 Замечание: Отметим, что неравенство (2) можно
записать в виде P(|x-MX|<ε)≥1- |
|
|
|
34(4)Свойства коэффициента корреляции. 1.Коэффициент
корреляции по абсолютной величине не
превосходит единицы, т.е.
Док-во
: Т.к. согласно св-ву 7 ковариации
∣Kxy∣≤σxσy
, то
2.Если
СВ X
и Y
независимы, тогда по сво-ву 3 ковариации
Kxy=0,
отсюда, что
3.Если
СВ X
и Y
связнаы линейной зависимостью, т.е.
Y=aX+b,
a≠0,
то
4.
Если
Замечание2:
Для
независимых СВ
|
|
|
|
|
|
|
|
) |
|
|
|
|

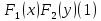

 ,
тогда Р[(X<x)(Y<y)]=Р(X<x)*Р(Y<y). Значит
, СВ X
и Y
независимы.
,
тогда Р[(X<x)(Y<y)]=Р(X<x)*Р(Y<y). Значит
, СВ X
и Y
независимы.
 (xipij),
MY=
(xipij),
MY= (yjpij)
(1), если (X,Y)
– ДДСВ и MX=
(yjpij)
(1), если (X,Y)
– ДДСВ и MX= MY=
MY= (2)
если (X,Y)
–НДСВ.
(2)
если (X,Y)
–НДСВ.
 ,
DY=
,
DY= (3) если (X,Y)
– ДДСВ и DX=
(3) если (X,Y)
– ДДСВ и DX= DY=
DY= (4) если (X,Y)
– НДСВ.
(4) если (X,Y)
– НДСВ. ковариацию часть удобно вычислить по
формуле Kxy=cov(X,Y)=M(X,Y)-MX*MY
В самом деле, запишем Kxy=
M[(X-MX)(Y-MY)]=M(XY-YMX-XMY+MXMY)=M(XY)-MYMX-MXMY+MXMY=M(XY)-MXMY
ковариацию часть удобно вычислить по
формуле Kxy=cov(X,Y)=M(X,Y)-MX*MY
В самом деле, запишем Kxy=
M[(X-MX)(Y-MY)]=M(XY-YMX-XMY+MXMY)=M(XY)-MYMX-MXMY+MXMY=M(XY)-MXMY (1)
(1)

 (2)
(2)
 сходятся по вероятности к А, если для
∀ε>0
D(|
сходятся по вероятности к А, если для
∀ε>0
D(| |<ε)→1
|<ε)→1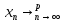 A
A
 сущ. число С>0 такое, что D
сущ. число С>0 такое, что D ,
то для ∀ε>0
,
то для ∀ε>0 (1),
т.е. среднее арифметическое этих СВ
сходится по вероятности к среднему
арифметическому их МО
(1),
т.е. среднее арифметическое этих СВ
сходится по вероятности к среднему
арифметическому их МО

 ,
то
,
то
 Тогда
применяя СВ
Тогда
применяя СВ
 =
=
 неравенство Чебышева (см. билет 35)
имеем
неравенство Чебышева (см. билет 35)
имеем
 Переходя
к пределу при n
Переходя
к пределу при n и учитывая. Что вероятность события
не превосходит единицы, получаем
и учитывая. Что вероятность события
не превосходит единицы, получаем
 независимы, одинаково распред. имеют
конечное математическое ожидание
M
независимы, одинаково распред. имеют
конечное математическое ожидание
M =a
и дисп. D
=a
и дисп. D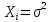 i=1..n
Тогда функция распределения
центрированной и нормированной суммы
этих СВ стрем. равномерно по x∈(-∞;+∞)
при n→∞
к функции распределения станд-й норм-й
СВ
i=1..n
Тогда функция распределения
центрированной и нормированной суммы
этих СВ стрем. равномерно по x∈(-∞;+∞)
при n→∞
к функции распределения станд-й норм-й
СВ
 )
)


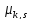 порядка k+s
двум. СВ
порядка k+s
двум. СВ



 2-х СВ X
и Y
называется
2-х СВ X
и Y
называется

 Y)=DX+DY
Y)=DX+DY 2
Kxy
2
Kxy
 Y)=M[(X+Y)-M(X+Y)]2=M[(X-MX)+(Y-MY)]2=M(X-MX)2+2M[(X-MX)(Y-MY)]+M(Y-MY)2=DX+2Kxy+DY
Y)=M[(X+Y)-M(X+Y)]2=M[(X-MX)+(Y-MY)]2=M(X-MX)2+2M[(X-MX)(Y-MY)]+M(Y-MY)2=DX+2Kxy+DY ,
или φ(x,y)=
,
или φ(x,y)=
 ,
интегрируем данное равенство по х и
по y,
получаем
,
интегрируем данное равенство по х и
по y,
получаем ,
т.е.
F(x,y)=
,
т.е.
F(x,y)= . На
основании теор.1 заключаем, что СВ X
и Y
независимы.
. На
основании теор.1 заключаем, что СВ X
и Y
независимы. )(Y=
)(Y= )])=P(X=
)])=P(X= )P(Y=
)P(Y= )
, I
от 1 до n,
J
от 1 до m.
(без док.)
)
, I
от 1 до n,
J
от 1 до m.
(без док.) ,
DXi=σ2
, то для любого
,
DXi=σ2
, то для любого

 ,
т.е. среднее арифметическое СВ сходится
по вероятности к МО , а
,
т.е. среднее арифметическое СВ сходится
по вероятности к МО , а

 (MX1+MX2+..+MXn)=
(MX1+MX2+..+MXn)= (a+a+a..+a)=a,
а дисперсия СВ
(a+a+a..+a)=a,
а дисперсия СВ
 равны числу σ2
,
т.е. ограничены, то применяя ранее
доказанную теорему, получаем
равны числу σ2
,
т.е. ограничены, то применяя ранее
доказанную теорему, получаем

 имеет место
имеет место
 т.е относительная частота υ(А)=
т.е относительная частота υ(А)=
 событие А сходится к вероятности Р
события А:
событие А сходится к вероятности Р
события А:
 ,
т.к. область интегрирования
,
т.к. область интегрирования
 , можно записать в виде (
, можно записать в виде ( или
или
 ≥1
≥1 1/
ε2
1/
ε2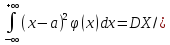 ε2
ε2 (3)
(3) ≤1
или -1≤
≤1
или -1≤ ≤1
≤1 =
= ≤
≤ =1
=1 =
=
 =1
, причем
=1
, причем
 =1,
при а>0,
=1,
при а>0,
 =-1,
при а<0 Без док-ва.
=-1,
при а<0 Без док-ва. =1
, то СВ X
и Y
связаны линейной функциональной
зависимостью. Без док-ва.
=1
, то СВ X
и Y
связаны линейной функциональной
зависимостью. Без док-ва. =0
для линейно связанных
=0
для линейно связанных
 =1,
в остальных случаях -1≤
=1,
в остальных случаях -1≤ ≤1.
Говорят, что СВ связаны положительной
корреляцией, если
≤1.
Говорят, что СВ связаны положительной
корреляцией, если
 >0,
отрицательной, если
>0,
отрицательной, если
 >0
>0