19. Метод k-средних в кластерном анализе.

Задача кластерного анализа носит комбинаторный характер. Прямой способ решения такой задачи заключается в полном переборе всех возможных разбиений на кластеры и выбора разбиения, обеспечивающего экстремальное значение функционала. Такой способ решения называют кластеризацией полным перебором. Аналогом кластерной проблемы комбинаторной математики является задача разбиения множества из nобъектов наmподмножеств. Число таких разбиений обозначается черезS(n,m) и называется числом Стирлинга второго рода. Эти числа подчиняются рекуррентному соотношению:.

При больших n.

Из этих оценок видно, что кластеризация полным перебором возможна в тех случаях, когда число объектов и кластеров невелико.

К решению задачи кластерного анализа могут быть применены методы математического программирования, в частности динамического программирования. Хотя эти методы, как и полный перебор, приводят к оптимальному решению в классе всех разбиений, для задач практической размерности они не используются, поскольку требуют значительных вычислительных ресурсов. Ниже рассматриваются алгоритмы кластеризации, которые обеспечивают получение оптимального решения в классе, меньшем класса всех возможных разбиений. Получающееся локально-оптимальное решение не обязательно будет оптимальным в классе всех разбиений.

Наиболее широкое применение получили алгоритмы последовательной кластеризации. В этих алгоритмах производится последовательный выбор точек-наблюдений и для каждой из них решается вопрос, к какому из mкластеров ее отнести. Эти алгоритмы не требуют памяти для хранения матрицы расстояний для всех пар объектов.

Остановимся на наиболее известной и изученной последовательной кластер-процедуре – методе k-средних (k-means). Особенность этого алгоритма в том, что он носит двухэтапный характер: на первом этапе в пространствеЕ_nищутся точки – центры клacтеров, а затем уже наблюдения распределяются по тем кластерам, к центрам которых они тяготеют. Алгоритм работает в предположении, что числоmкластеров известно. Первый этап начинается с отбораmобъектов, которые принимаются в качестве нулевого приближения центров кластеризации. Это могут быть первые mиз списка объектов, случайно отобранные m объектов, либоmпопарно наиболее удаленных объектов.

Каждому центру приписывается единичный вес. На первом шаге алгоритма извлекается первая из оставшихся точек (пометим ее как) и выясняется, к какому из центров она оказалась ближе всего в смысле выбранной метрикиd. Этот центр заменяется новым, определяемым как взвешенная комбинация старого центра и новой точки. Вес центра увеличивается на единицу. Обозначим черезn-мерный вектор координатi-го центра на-м шаге , а через– вес этого центра. Пересчет координат центров и весов на-м шаге при извлечении очередной точки осуществляется следующим образом:

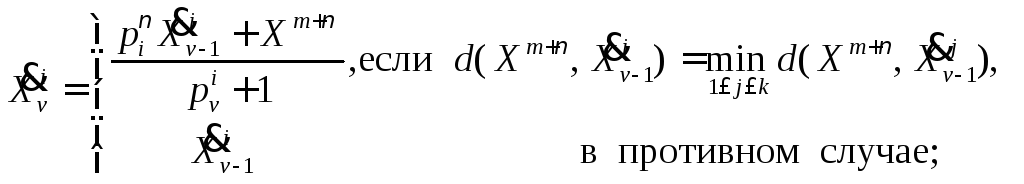(9.5)

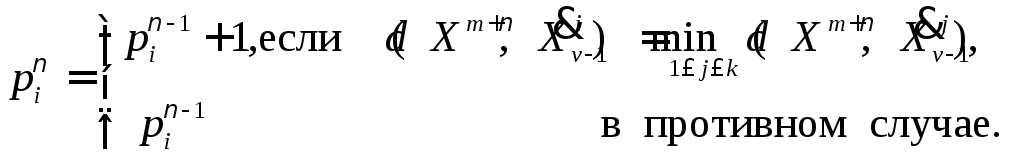(9.6)

При достаточно большом числе классифицируемых объектов имеет место сходимость векторов координат центров кластеризации к некоторому пределу, то есть, начиная с некоторого шага, пересчет координат центров практически не приводит к их изменению.

Если в конкретной задаче устойчивость не имеет места, то производят многократное повторение алгоритма, выбирая в качестве начального приближения различные комбинации из mточек.

После того как центры кластеризации найдены, производится окончательное распределение объектов по кластерам: каждую точку ,i=1,2,…,Nотносят к тому кластеру, расстояние до центра которого минимально.

Описанный алгоритм допускает обобщение на случай решения задач, для которых число кластеров заранее неизвестно. Для этого задаются двумя константами, одна из которых называется мерой грубости, а втораяΨ₀– мерой точности.

Число центров кластеризации полагается произвольным (пусть ), а за нулевое приближение центров кластеризации выбирают произвольныеточек. Затем производится огрубление центров заменой двух ближайших центров одним, если расстояние между ними окажется меньше порога. Процедура огрубления заканчивается, когда расстояние между любыми центрами будет не меньше. Для оставшихся точек отыскивается ближайший центр кластеризации, и если расстояние между очередной точкой и ближайшим центром окажется больше, чемΨ₀, то эта точка объявляется центром нового кластера. В противном случае точка приписывается существующему кластеру, координаты центра которого пересчитываются по правилам, аналогичным (9.5), (9.6).