
Решения / 7 семинар
.doc|
Семинар №7 «Случайные величины» (1 из 12) |
Семинар №7 «Случайные величины» (2 из 12) |
|
1.
В лотерее имеется 10 билетов, из
которых один выигрышный. Размер
выигрыша 10 рублей; стоимость билета
1 рубль. Найти распределение случайной
величины , равной
чистому выигрышу участника лотереи,
который вытаскивает билет первым.
Указание. Для удобства
будем считать, что билеты занумерованы
и что билет 1– выигрышный. ={1,
2,…,10}. (1)=9, (j)=
–1, j= Решение: Выигрыш 1 билет из 10-ти. Тогда чистый выигрыш либо 9, либо -1, следовательно P{=9}=1/10, P{= –1}=9/10. 2. Из ящика с 10 одинаковыми карточками, на которых написаны цифры 0,1,…,9 два раза с возвращением вынимаются по одной карточке. Введем случайные величины: 1– цифра на 1-й карточке, 2– цифра на 2-й карточке, = 1+2. Найти распределение случайных величин 1, 2, . Найти вероятность события {2}. Нарисовать график функции распределения с.в. 1. Указание. ={ (i, j): i, j =0, 1,…,9}. 1(i, j)= 1(i), 2(i, j)= 2(j), (i, j)= i+j. {=k}={(0, k), (1, k–1),…, (k, 0)}, 0k9; {=9+k}= {(k, 9), (k+1, 8),…, (9, k)}, 1k9.Ответ:P{1=k}=P{2=k}=0.1,P{=k}=(k+1)/100,0k9, P{=k}= =(10– k)/100, 1k9, P{2}=0.06. Решение: Цифра на 1-ой
карточке: P{1}=
1/10, цифра на 2-ой: P{2}=1/10.
Сумма цифр равна k,тогда
возможны случаи: (0,k),(1,k-1),…,(k-1,1),
(k,0) – их количество
k+1-или
(9,k),(8,k+1),…,(k+1,8),(k,9).
Тогда P{1+2=k}=
k+1/100 ( т.к. всего
100 способов);
=1/100 + 2/100 +
3/100= 6/100; P{=k)=(10-k)/100
;
3. В опыте, описанном в задаче 2, введем случайную величину , равную числу четных чисел на вынутых карточках. Величины 1 и 2 определим равенствами: 1=1, если на 1-й карточке четная цифра, и 1=0 в противном случае; 2=1, если на 2-й карточке четная цифра, и 2=0 в противном случае. Найти законы распределения 1, 2, .
|
Проверить, что =1+2. Нарисовать график функции распределения с.в. . Ответ: P{=0}=P{=2}=1/4, P{=1}=1/2, P{1=0}=P{2=0}=1/2. Решение:
4. Брошено две игральные кости. Найти закон распределения случайной величины , равной сумме выпавших очков. Найти вероятность событий: {4}, {>4}. Ответ: P{=k}=(k–1)/36, 2k7, P{=k}=(13–k)/36, k>7. P{4}=1/6. Решение:
=(13-k)/36,
5.
Из урны, содержащей n
шаров, среди которых m
белых и n –m
черных, извлекают k
шаров. Определить закон распределения
числа белых шаров,
среди выбранных по схеме случайного
выбора а) без возвращения; б) с
возвращением. а) гипергеометрическое
распределение; б)
Решение: Всего n
шаров, m белых и n-m
чёрных. Извлекаем k
шаров. а) Необходимо вытащить : i
белых шаров из m белых,
(k-i) чёрных
из (n-m)
чёрных. Всего вариантов вытаскивания
:
|
|
Семинар №7 «Случайные величины» (3 из 12) |
Семинар №7 «Случайные величины» (4 из 12) |
|
Решение: Всего n
шаров, m белых и n-m
чёрных. Извлекаем k
шаров. а) Необходимо вытащить : i
белых шаров из m белых,
(k-i) чёрных
из (n-m)
чёрных. Всего вариантов вытаскивания
:
б) Схема
Бернулли: k испытаний,
i успехов,
6. а) Случайная величина принимает значения x1= –1, x2=0, x3=1 с вероятностями c, 2c, 3c. Найти c. б) Найти
закон распределения случайной величины
, если
в) Найти
закон распределения случайной величины
, если
Решение: а) б)
= с в)
|
7. Для случайной величины , имеющей а) геометрическое распределение вероятностей, найти P{k} (воспользоваться геометрической прогрессией); б) пуассоновское распределение, найти P{>0}; в) биномиальное распределение с n=5, p=1/3 , найти P{24}. Ответ: (1–p)k–1; 1–e–, 130/243. Решение: а) =
8. Дискретная случайная величина задана законом распределения P{= –1}=0.3; P{= –2}=0.1, P{= 1}=0.2, P{= 2}=0.4, найти закон распределения случайной величины =2. Ответ: P{=1}= P{=4}=1/2. Решение:
9.
Задана плотность распределения (x)
случайной величины ,
принимающей значения из (0, +).
Найти плотность распределения (x)
случайной величины ,
если а) =e–
; б)
=ln();
в) =3
; г) =1/2;
д) =
|
|
Семинар №7 «Случайные величины» (5 из 12) |
Семинар №7 «Случайные величины» (6 из 12) |
|
Решение: а)
10.
Задана плотность распределения (x)
случайной величины ,
принимающей значения из (–,
+).
Найти плотность распределения (x)
случайной величины ,
если а) =2;
б) = Ответ:
а)
Решение: a)
|
б)
= в)
-> =
|
|
Семинар №7 «Случайные величины» (7 из 12) |
Семинар №7 «Случайные величины» (8 из 12) |
|
11. На квадрат ={(u, v): | u| 1, | v | 1} брошена точка. Определим случайные величины , , :
Найти: а) вероятность событий P{>0}, P{=1}, P{>1}; б) функцию распределения и плотность распределения с.в. ; в) закон распределения с.в. . Ответ: P{>0}=1/2, P{=1}=/16, P{>1}=1–/4, F(x)= (x+1)/2, (x)=1/2, –1x1. Решение:
a)
|
= 12. Плотность распределения с.в. задана формулой
Найти:
а) постоянную c;
б) плотность распределения
Ответ:
c
=1/2, (x)=
Решение: а)
|
|
Семинар №7 «Случайные величины» (9 из 12) |
Семинар №7 «Случайные величины» (10 из 12) |
|
=> в)
13. Построить пример такого абсолютно непрерывного распределения случайной величины , задаваемого плотностью распределения (x), и такое непрерывной функции g(x), что распределение случайной величины =g() не вырождено и дискретно. Нет решения. 14.
Случайная величина
имеет показательное распределение с
параметром :
P{x}=1–ex
(x0).
Найти плотности распределения случайных
величин: a)
Ответ:
Решение:
Из
нормировки вытекает, что
|
г)
x
|
|
Семинар №7 «Случайные величины» (11 из 12) |
Семинар №7 «Случайные величины» (12 из 12) |
|
15.
Случайная величина
равномерно распределена на [0,1]. Найти
плотность распределения случайных
величин: a)
Ответ:
1/2 (x[1,3]);
e–x
(x>0);
Решение: По
условию =>
б)
в) 16.
Случайная точка B
имеет равномерное распределение на
окружности x2+(y–a)2=r2
с центром в точке A=(0,
a),
а случайная точка C=(,
0) является пересечением оси абсцисс
с прямой, проходящей через A
и B.
Найти функцию распределения и плотность
распределения случайной величины .
(Распределение
называется распределением Коши).
Ответ:
Решение: Пусть Vn– n-мерное векторное пространство над полем из двух |
элементов
GF(2).
Операцию сложения в GF(2)
будем обозначать .
Вектор a=(a1,…,
an)
будем отождествлять с числом
Но a может быть <0 =>
17. Пусть a, b– случайные независимые векторы с равномерным распределением на Vn, c=a+b (mod 2n). Доказать,
что
Решение: Для того,
чтобы
+1/2))]=// 1-ая сумма ¼+1/2-m+1 разряд, следующая m+2, и т.д. до n-ого разряда//= =1/4+1/8+1/16+…+1/4
+ |

 .
. -
гипергеометрическое распределение.
-
гипергеометрическое распределение. -
гипергеометрическое распределение.
-
гипергеометрическое распределение. .
.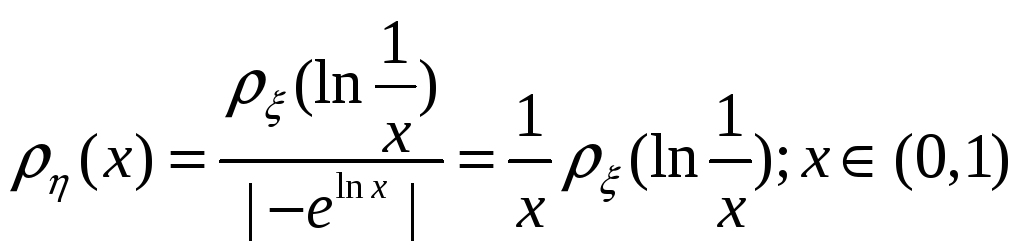 .
б)
.
б)
 .г)
.г)
 .д)
.д)
 .
.
 ,
,
 =>
=> ,
,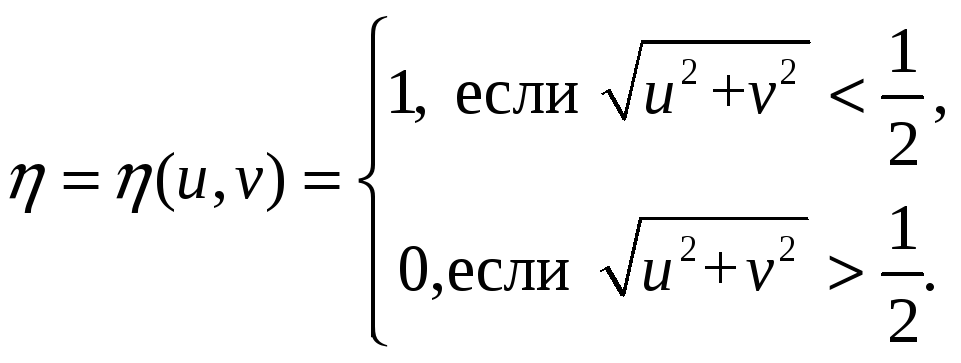






 ;
;







 =
=