Решения / 11 семинар
.doc|
СЕМИНАР №11 «Закон распределения и характеристики n-мерных случайных величин II» (1 из 16) |
СЕМИНАР №11 «Закон распределения и характеристики n-мерных случайных величин II» (2 из 16) |
|
1. Случайная точка (, ) равномерно распределена в квадрате B={0x, y 4}. Найти ,(x, y), F(x), P{–2<<2, 1<3}. Указание:
P{–2<<2,
1<3}= Ответ. ,(x, y)=1/16 при (x, y)B, ,(x, y)=0 при (x, y)B; P{–2<<2, 1<3}=1/4; F(x)=0 при x0, F(x)=x/4 при 0<x4, F(x)=1 при x>4. Решение:
y
|
2.
Случайная точка (,
)
равномерно распределена внутри круга
B={(x,
y)|
Ответ:
,(x,
y)=1/r2
при (x, y)B,
,(x,
y)=0 при (x,
y)B;
(x)= Решение:
a).
|
|
СЕМИНАР №11 «Закон распределения и характеристики n-мерных случайных величин II» (3 из 16) |
СЕМИНАР №11 «Закон распределения и характеристики n-мерных случайных величин II» (4 из 16) |
|
И
б).
Если
|
3. Совместная плотность распределения случайных величин , имеет вид а)
Найти c, (x), P{>2}. б)
Найти c, (x), P{>1}. Ответ: а) c=1/216, (x)=(x+3)/36 при x[0, 6], (x)=0 при x[0, 6], P{>2}=11/18; б) c=3/32, (y)=3y2/16 +1/4 при y[0, 2], (y)=0 при y[0, 2], P{>1}=11/16. Решение: Нет решения. 4. Совместная плотность распределения случайных величин , имеет вид а)
б)
в)
|
|
СЕМИНАР №11 «Закон распределения и характеристики n-мерных случайных величин II» (5 из 16) |
СЕМИНАР №11 «Закон распределения и характеристики n-мерных случайных величин II» (6 из 16) |
|
Зависимы или нет случайные величины , . Найти (x). Указание:
а) Найти (x),
(y)
и проверить, что
Ответ: а) (x)=2x при x[0, 1], (x)=0 при x[0, 1], независимы;
б)–в) (x)= Решение: а)
Найдем
б)
|
в)
5. Совместная плотность распределения случайных величин , имеет вид а)
б)
Найти
Ответ: a)
б)
|
|
СЕМИНАР №11 «Закон распределения и характеристики n-мерных случайных величин II» (7 из 16) |
СЕМИНАР №11 «Закон распределения и характеристики n-мерных случайных величин II» (8 из 16) |
|
Решение: а)
Соответственно
б)
Соответственно
6. Случайные величины , независимы и а)
б) равномерно распределены на отрезке [0, 1]. в)
|
Найти
Указание.
б) F–(y)=P{–y}=1–P{<–y}
и –(y)=1
при y[–1,
0], –(y)=0
при y[–1,
0],
Ответ: a)
б)
Решение: а)
Получаем:
б)
Указания:
|
|
СЕМИНАР №11 «Закон распределения и характеристики n-мерных случайных величин II» (9 из 16) |
СЕМИНАР №11 «Закон распределения и характеристики n-мерных случайных величин II» (10 из 16) |
|
Имеем:
в)
Соответственно
7. Пусть , – независимые случайные величины с функциями распределения F(x) и F(y) соответственно. Найти функцию распределения случайной величины а) =max(, ); б) =min(, ). Указание: F(z)=P{ z}= P{ max(, ) z}= P{ z , z}. Ответ: а) F(z)=F(z)F(z); б) F(z)=1–(1–F(z))(1–F(z)).
|
Решение: ]
а)
б)
8. Совместная плотность распределения случайных величин , имеет вид
Найти функцию распределения случайной величины а) =max(, ); б) =min(, ). Ответ:
Решение:
а).
|
|
СЕМИНАР №11 «Закон распределения и характеристики n-мерных случайных величин II» (11 из 16) |
СЕМИНАР №11 «Закон распределения и характеристики n-мерных случайных величин II» (12 из 16) |
|
Соответственно
б).
Соответственно
При
10. Совместная плотность распределения случайных величин , имеет вид
Пусть =2. Найти E, E, cov(, ). Ответ: E=2/3, E=1/3, cov(, )=0. Решение:
|
11. Совместная плотность распределения случайных величин , имеет вид
Найти E(1–). Ответ: 1/6. Решение:
12. Совместная плотность распределения случайных величин , имеет вид
Найти c, E(2 +2). Ответ: c=3/8, E(2 +2)=14/5.
|
|
СЕМИНАР №11 «Закон распределения и характеристики n-мерных случайных величин II» (13 из 16) |
СЕМИНАР №11 «Закон распределения и характеристики n-мерных случайных величин II» (14 из 16) |
|
Решение:
13. Совместная плотность распределения случайных величин , имеет вид
Найти E, D, ковариацию и корреляцию случайных величин , . Ответ: E=7/12, D=11/144, cov(, )= –1/144, (, )= –1/11.
|
Решение:
14. Непрерывная двумерная случайная величина (, ) распределена равномерно в круге радиуса r с центром в начале координат. Доказать, что , зависимы, но не коррелированны (cov(, )=0). Решение:
|
|
СЕМИНАР №11 «Закон распределения и характеристики n-мерных случайных величин II» (15 из 16) |
СЕМИНАР №11 «Закон распределения и характеристики n-мерных случайных величин II» (16 из 16) |
|
Доказать:
15. Двумерное распределение случайных величин , задано функцией распределения
Найти
Указание.
Показать, что ,
равномерно распределены на [0, 1] и
P{=}=1.
Ответ: 1–
|
Решение:
|




 при
|x|r,
(x)=0
при |x|>r.
при
|x|r,
(x)=0
при |x|>r.






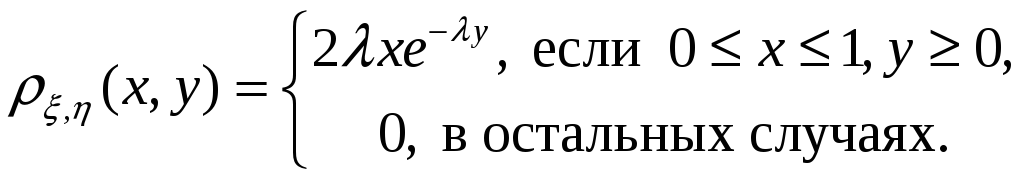

 является
плотностью стандартного нормального
распределения и, следовательно,
является
плотностью стандартного нормального
распределения и, следовательно,
 ,
независимы.
,
независимы.











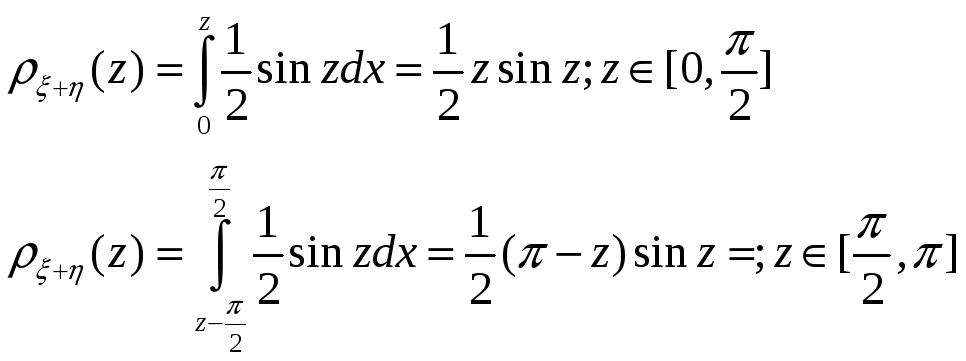

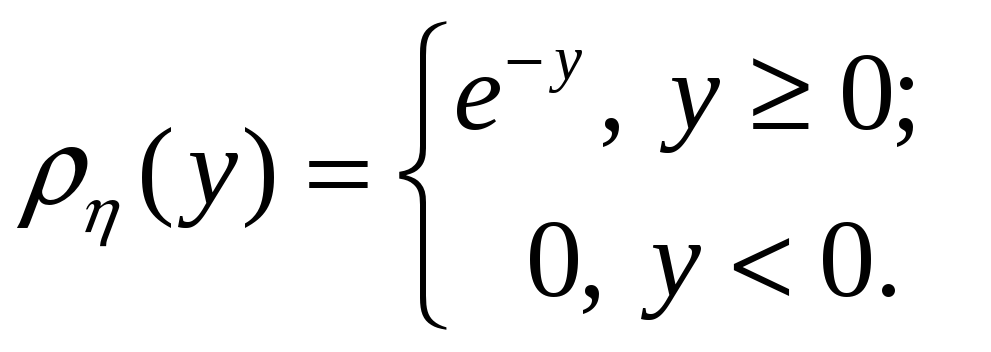







 и
и



















 .
.