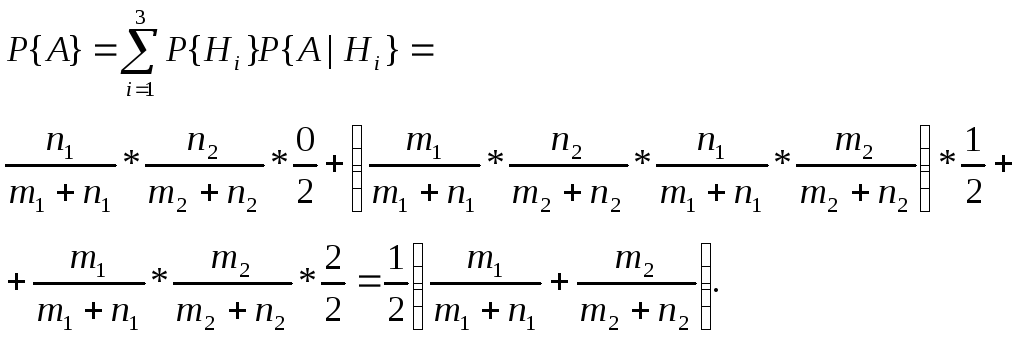Решения / 5 семинар

Семинар №5 «Формула полной вероятности. Формула Байеса»

(1 из 10)

Семинар №5 «Формула полной вероятности. Формула Байеса»

(2 из 10)

1. Среди четырех неразличимых по внешнему виду урн три урны имеют одинаковый состав – 2 белых и 1 черный, а в четвертой урне–один белый и один черный шар. Из случайно выбранной урны случайно вынимается шар. Найти вероятность того, что

а) этот шар–белый. б) была выбрана урна с составом шаров «2 белых и 1 черный», если известно, что вынутый шар оказался белым.

Указание. В качестве гипотез можно выбрать состав шаров выбранной урны:

B₁={в выбранной урне 2 белых и 1 черный шар},

B₂={в выбранной урне 1 белый и 1 черный шар},

A={вынут белый шар}.

Найти P{A|B₁}=2/3, P{A|B₂}=1/2, P{B₁}=3/4, P{B₂}=1/4.

Ответ: P{A}=5/8, P{B₁|A}=4/5.

Решение:

B₁ ={в выбранной урне 2 белых и 1черный}

B₂ ={в выбранной урне 1 белый и 1 черный}

P{A|B₁}=2/3, P{A|B₂}=1/2, P{B₁}=3/4, P{B₂}=1/4;

P{A}=P{B_k}*P{A|B_k}=P{B₁}*P{A|B₁}+P{B₂}*P{A|B₁}=

=3/4*1/2+1/4*1/2=5/8

P{B₁|A}==4/5

2. В урну, содержащую n шаров, опущен белый шар. Какова вероятность извлечь белый шар, если все предположения о первоначальном составе шаров по цвету равновозможны.

Указание. Гипотеза H_k– в урне k белых шаров (k=), A={вынут белый шар}. Ответ: .

Решение:

Гипотеза H_k – k белых шаров k=(0,1)

A={вытянут белый шар}

P{H_k}=1;

P{A|H_k}=;

P{A}=.

3. В тире имеются 5 ружей, вероятности попадания из которых равны соответственно 0,5; 0,6; 0,7; 0,8; 0,9. Определить вероятность попадания при одном выстреле, если стреляющий берет одно из ружей случайно. Ответ: 0,7.

Решение:

5 ружей

– вероятность выбрать m-ное ружье;

4. В первой урне находится 1 белый и 9 черных шаров, а во второй– 1 черный и 5 белых шаров. Из каждой урны по схеме случайного выбора без возвращения удалили по одному шару, а оставшиеся шары ссыпали в третью урну. Найти вероятность того, что шар, вынутый из урны, окажется белым. Ответ: 0,36

Решение:

1 урна: 1 белый, 9 черных;

2 урна: 1 черный, 5 белых.

B₁={из первой урны – белый, из второй - белый};

B₂={из первой урны – черный, из второй - черный};

B₃={из первой урны – белый, из второй - черный};

B₄={из первой урны – черный, из второй - белый};

P{A}=

Семинар №5 «Формула полной вероятности. Формула Байеса»

(3 из 10)

Семинар №5 «Формула полной вероятности. Формула Байеса»

(4 из 10)

5. Из урны, содержащей m белых и n–m черных шаров, утеряно r шаров. Сравнить вероятности извлечения белого шара а) до утери; б) после утери при r =1; в) после утери при r>1.Указание в), .

Ответ: а),б),в) m/n.

Решение:

m - белых;

(n-m) – черных;

r – утерянных.

a) до потери m – белых, всего n P(A)=m/n.

б) после потери r=1

B₁={утеряли белый};

B₂={утеряли черный}

P{A}= + =m/n*(m-1)/(n-1)+(n-m)/n*m/(n-1)=m/n.

в) H={выпал белый при r>1};

H_k={среди потерянных r шаров k белых}

P{A}=;

P{H_k}=;

P{A|H_k}=;

P{A}=.

6. В двух урнах находится соответственно m₁ и m₂ белых и n₁ и n₂ черных. Из каждой урны случайно извлекается один шар, а затем из этих двух шаров случайно берется один. Какова вероятность, что

этот шар белый? Указание: H₁– среди извлеченных шаров нет белых, H₂– один белый, H₃– оба белых. Ответ: .

Решение:

H₁={извлеченные шары черные};

H₂={извлеченные шары и белые и черные};

H₃={извлеченные шары белые};

A={шар белый}.

7. Посох волшебника может принадлежать к одному из трех типов магий (черной, белой и смешанной) с вероятностями p₁=p₃=0,25 и p₂=0,5. Вероятность того, что посох израсходует данное ему количество магической силы, соответственно равна 0,1; 0,2 и 0,4. Определить вероятность того, что посох израсходует данное ему количество магической силы. Ответ: 0,225.

Решение:

По формуле полной вероятности:

8. Вероятность обнаружения приведений в старинном замке равна 0,8. Вероятность принять замок без приведений за замок с приведениями равна 0,05. Известно, что доля старинных замков с приведениями равна 0,05. Найти условную вероятность, что в замок нет приведений, если он был признан замком с приведениями. Указание: H₁–в замке есть приведения, H₂–замок без приведений, А–замок с приведениями. Ответ: 19/35.

Семинар №5 «Формула полной вероятности. Формула Байеса»

(5 из 10)

Семинар №5 «Формула полной вероятности. Формула Байеса»

(6 из 10)

Решение:

H₁={в замке есть приведения}

P{H₁}=0,05;

H₂={замок без приведений}

P{H₂}=0,95;

A={замок с приведениями}

По формуле Байса

P{H₂|A}=

9. Долговременная практика рекламирования новых видов амулетов показала, что после проведения рекламной компании 5% эльфов и 10% людей желали бы приобрести новый вид кольца удачи, а остальные покупают прежние неусовершенствованные кольца. Число эльфов и людей в городе Приграничном соотносятся как 4:6 и все они покупают магические кольца-амулеты. Какова вероятность, что случайно выбранный покупатель, приобретший новый вид кольца удачи будет человеком. Ответ: 3/4.

Решение:

H₁={житель является эльфом}

P{H₁}=0,4;

H₂={житель является человеком}

P{H₂}=0,6;

A={покупателдь выбрал новые кольца}

P{A|H₁}=0,05, P{A|H₂}=0,1.

По формуле Байса

P{H₂|A}=

10. Имеются n урн, в каждой из которых по m белых и по k черных шаров. Из первой урны случайно извлекается один шар и перекладывается во вторую. Затем из второй урны случайно

извлекается шар и перекладывается в третью урну и.т.д. Определить вероятность извлечения после такого перекладывания белого шара из последней урны. Указание: –из j-й извлекается белый шар, –из j-й извлекается черный шар. Найти P{}, P{}, P{}, P{}. Применить метод математической индукции, положив P{}=, P{}=. Ответ: .

Решение:

n-урн, в каждой m – белых, n – черных.

={из j-ой урны взяли белый шар};

={из j-ой урны взяли черный шар};

P{} = P{}=;

P{}= =

P{} =

Далее показываем что и P{} и p{} равно и соответственно.

А следовательно и при j=n P{}=.

11. В объединенной армии темных сил 70% вампиров и 30% горгулий. Среди вампиров 10% титулованных особ, а среди горгулий– 5% титулованных особ. Все титулованные особы по очереди каждый вечер дежурят по армии. Найти вероятность, что в случайно выбранный день дежурит вампир. Ответ: 14/170,823.

Решение:

H₁={воин вампир}

P{H₁}=0,7;

Семинар №5 «Формула полной вероятности. Формула Байеса»

(7 из 10)

Семинар №5 «Формула полной вероятности. Формула Байеса»

(8 из 10)

H₂={воин гаргулья}

P{H₂}=0,3;

A={воин титулованная особа}

P{A|H₁}=0,1, P{A|H₂}=0,05.

По формуле Байса

P{H₁|A}=

12. По каналу связи может быть передана одна из трех последовательностей букв ААА, ВВВ, ССС с равными вероятностями. При передаче каждая буква независимо от остальных принимается правильно с вероятностью p, и принимается ошибочно за каждую из двух других с вероятностью q. Найти вероятность того, что было передано ААА, если принято ВАА. Указание: –j-я буква искажена, –j-я буква неискаженна, P{AAA| BAA}=0,20,80,8. Ответ: 16/21.

Решение:

={j-ая буква искомая};

={j-ая буква не искомая};

P{AAA|BAA}=P{}P{}P{}=p²q;

P{BBB|BAA}= P{}P{}P{}=pq²;

P{CCC|BAA}= P{}P{}P{}=q³;

P{BAA|AAA}=

13. По каналу связи передается одна из последовательностей букв АААА, ВВВВ, СССС с вероятностями p₁, p₂, p₃ (p₁+ p₂+ p₃=1). Каждая передаваемая буква принимается правильно с вероятностью  и с вероятностями и принимается за две другие буквы. Предполагается, что буквы искажаются независимо друг от

друга. Найти вероятность того, что было передано АААА, если принято ABCA. Ответ: .

Решение:

H₁={AAAA};

H₂={BBBB};

H₃={CCCC};

P{ABCA}=

P{AAAA|ABCA}=

14. При секретном сканировании местности со спутника вероятность обнаружить существо внеземного происхождения равна 1–. Вероятность принять человека за инопланетянина равна . Доля пришельцев по отношению ко всему населению Земли равна . а) Найти условную вероятность, что человек землянин, если он был признан пришельцем при сканировании. б) Вычислить условную вероятность при следующих числовых значениях 1–=0,9; =0,01; =0,01.

Ответ: .

Решение:

B₁={житель земли}

B₂={пришелец}

A={обнаружен}

P{B₁}=; P{B₂}=1-;

P{A|B₁}=1-; P{A|B₂}=;

P{A}=

P{B₂|A}=

Семинар №5 «Формула полной вероятности. Формула Байеса»

(9 из 10)

Семинар №5 «Формула полной вероятности. Формула Байеса»

(10 из 10)

15. Произведено три независимых испытания, в каждом из которых событие А происходит с вероятностью 0,2. Вероятность появления другого события В зависит от числа появлений события А: при однократном появлении события А эта вероятность равна 0,1; при двукратном– 0,3; при трехкратном– 0,7; если событие А не имело место ни разу, то событие B невозможно. Определить наивероятнейшее число появлений события А, если событие B имело место. Ответ: 1.

Решение:

Три испытания: соб. ;

Произошло событие B, тогда возможно: , т.е.

16. В вольном магическом сообществе n чародеев, из которых n_k (k=1, 2, 3) магов изучают искусство гипноза k-й год. Среди двух случайно выбранных чародеев оказалось, что один из них изучает гипноз дольше второго. Какова вероятность, что маг учится этому третий год. Указание. Гипотезы: Н₁– первый маг изучает гипноз первый год, Н₂– второй год. События: A– второй маг изучает гипноз дольше первого, B– второй маг изучает гипноз третий год. , . Ответ: .

Решение:

H₁={1ый маг изучает гипноз 1 год};

H₂={2ой маг изучает гипноз 1 год};

A={второй маг учит дольше первого}.

P{B|A}=