
Решения / 6 семинар
.doc|
Семинар №6 «Схема Бернулли. Полиномиальная схема» (1 из 12) |
Семинар №6 «Схема Бернулли. Полиномиальная схема» (1 из 12) |
|
1. Выписать все элементарные исходы схемы Бернулли с n=3 испытаниями и найти их вероятности, если вероятность успеха равна p. Найти вероятность событий: 1) A={успехи и неудачи чередуются}; 2) A={произошло ровно два успеха, причем не в соседних испытаниях}; 3) A={произошло четное число успехов}. Указание 1) A={УНУ, НУН}. Ответ: pq, p2q, q3+3p2q. Решение:
2. В
схеме Бернулли с n
испытаниями и вероятностью успеха
p найти вероятности
событий: 1) A={ни
одного успеха не произошло}; 2)
A={произошел хотя
бы один успех}; 3) Ak={успех
впервые произойдет на k-м
испытании}. Указание 3) Пусть Ci={успех
в i-м испытании}.
Тогда
Решение: 1) A1={ни одного успеха} P(A1)=(1-p)n=qn 2) A2={успех впервые на k-ом испытании} P(A2)=1-P(A1)=1-qn 3)
P(Ak)= 3.
Брошено 10 игральных костей. Найти
вероятности событий: A={выпало
ровно две 6}, B={выпала
хотя бы одна 6}. Указание. Воспользоваться
схемой Бернулли с n=10,
p=1/6 (десять игральных
костей– десять испытаний, выпадение
6– успех); A={10=2},
B={101},
Решение: 10 костей А={выпало ровно 2 шестерки} n=10 p=1/6 |
P(A)= B={выпала хоть 1 шестерка} B’={не выпало ни одной шестерки} P(B’)=(1-p)10=(5/6)10 P(B)=1-P(B’)=1-(5/6)10 4. Сколько нужно бросить игральных костей, чтобы вероятность выпадения хотя бы одной 1 была не меньше 0,9? Указание. Для произвольного n найти вероятность события {n1}, где n число выпавших 1, и разрешить соответствующее неравенство относительно n. Ответ: P{n1}=1–(5/6)n, нужно бросить 13 костей. Решение: A={выпала хоть одна} P(A) P(A)=1-(5/6)n 0,1 n 5. По каналу связи передается 20 знаков. Вероятность искажения равна 0,01. Найти вероятность того, что искажено не более двух знаков. Указание. Воспользоваться схемой Бернулли с n=20, p=0,01 и событие {n2}={n=0}+{n=1}+{n=2}, где n– число искажений. Ответ:0,9989 Решение: n=20 p=0,01 – вероятности искажений А=(не более 2-х знаков искажено) Р(А)=(1-p)n+p(1-p)n-1+p2(1-p)n-2=
0,9920+ 6. На уроке зельеварения в Хогвартсе ученики приготовили 10 зелий. Считая вероятность приготовления зелья из лягушек, равной p, а зелья из волчьей ягоды – q, определить вероятность того, что на данном уроке было сделано a) k зелий с лягушками; |
|
Семинар №6 «Схема Бернулли. Полиномиальная схема» (3 из 12) |
Семинар №6 «Схема Бернулли. Полиномиальная схема» (4 из 12) |
|
б) зелий с
лягушками не менее 3, но и не более 8.
Ответ а)
Решение: а) Воспользуемся схемой Бернулли, где n=10 и где k успехов Тогда
Р(А)= б) k=3,..,8 Р(B)= 7. В
полиномиальной схеме c
m=3, n=5
и вероятностями исходов p1,
p2 и p3
найти вероятность события {1=2,
2=1, 3=2}.
Ответ 30 Решение: m=3, n=5 p1,p2,p3 A={ Тогда Р(А)= 8. При встрече двух хоббитов шахматистов Фродо и Бильбо исходы одной партии «победа Фродо», «поражение Фродо» и «ничья» имеют вероятности соответственно 0,1; 0,1; 0,8. Найти вероятности того, что матч из 10 партий закончится следующим результатом: 2 победы Фродо, 1 победа Бильбо, а остальные ничьи. Указание. Воспользоваться полиномиальной схемой с n=10, m=3, p1=p2=0,1, p3=0,8. Найти вероятность события {1=2, 2=1, 3=8}. Ответ: 360(0,1)3(0,8)7. Решение: n=10, m=3, p1=p2=0,1, p3=0,8 { P= 9. На планете Орион-23 в году n месяцев. Музей истории планеты |
Земля собралось посетить n орионцев. Найти вероятность, что все их дни рождения приходятся на разные месяцы. Указание. Воспользоваться полиномиальной схемой с n=m, p1=…= pm. Найти вероятность события {1=1,…, m=1}. Ответ: m!/mm. Решение: n=m,
p1=p2=…=pm
. Тогда Р{ 10. В магазине «1000 магических мелочей» 40% покупателей приобрели метлу «Метеор-2004», 30% – ковер-самолет, 20%– волшебные палочки, а 10%–магические кольца. Какова вероятность, что в группе из 10 покупателей будет а) ровно 2, купивших метлу «Метеор-2004»? б) по крайней мере 2, купивших магические кольца? в) ровно один покупатель, купивший ковер-самолет, двое –волшебные палочки, пять– метлу «Метеор-2004» и три– магические кольца? Ответ: a) Решение: n=10, p1=0,4, p2=0,3, p3=0,2, p4=0,1 а) Р{ б)
Р{ в) { Р= 11.
Найти вероятность, что в 2n
испытаниях схемы Бернулли с вероятностью
успеха p появится
m+n
успехов и все испытания с четными
номерами закончатся успехом. Ответ:
|
|
Семинар №6 «Схема Бернулли. Полиномиальная схема» (5 из 12) |
Семинар №6 «Схема Бернулли. Полиномиальная схема» (6 из 12) |
|
Решение: 2n испытаний р- вероятность успеха P(m+n)= Если только четные, то n- испытания, (m+n)-n=m успехов P(m)= 12.
а) Из множества S={ б) Из
множества S={
в) Из множества S={ Указание. б) Множества A1,…, Ar попарно не пересекаются, если каждый элемент xS либо не включается ни в одно из r подмножеств, либо включается ровно в одно множество. Ответ: а)
(1–p2)m,
б) (rpqr–1+qr)m,
в)
Решение:
|
13. Каждую секунду с вероятностью p независимо от других моментов времени по дороге проезжает автомашина. Пешеходу для перехода дороги необходимо 3 с. Какова вероятность, что подошедший к дороге пешеход будет ожидать возможности перехода a) 3 c; б) 4 с; a) 5 c? Указание.
Рассмотреть схему Бернулли. Пусть Аt
–событие, состоящее в том, что в момент
времени t по дороге
мимо пешехода проезжает машина, t=1,2,…
События A1,
A2… независимы,
P{At}=p.
Выразить интересующее событие через
A1, A2…
{пешеход ожидает 4 с}= Решение: а) А - он будет ждать 3 секунды
|
|
Семинар №6 «Схема Бернулли. Полиномиальная схема» (7 из 12) |
Семинар №6 «Схема Бернулли. Полиномиальная схема» (8 из 12) |
|
б) А – ждёт 4 секунды т.е. в первые 3 секунды должна проехать какая-либо машина
в) 1) Первые 3
секунды должны быть заняты: 2) Если в первую
секунду едет машина, то потом опять
случай (1): 3)
=>A
– ждёт 5 секунд:
14.
В одном из матчей по квидичу в Хогвартсе
на первенство школы между командами
двух факультетов ничья не учитывалась,
и игра шла до тех пор, пока один из
участников матча не набирал 6 очков
(выигрыш– 1очко, проигрыш и ничья–
0). Считая участников матча одинаковыми
по силе, а результаты игр независимыми,
найти вероятность, что при таких
правилах в момент окончания матча,
проигравший наберет k
очков, k= Решение: Проводим 6+k испытаний: Необходимо рассмотреть 5+k испытаний: после 6+k испытаний игра заканчивается. А-проигравшая набрала k. А={проигравшая
набрала k в 5+k
играх} Вероятность
того, что первая команда за (5+k)
игр наберёт k очков,
равна:
Получаем в
последнем матче необходимо проиграть- |
15. Производятся 4 независимых опыта, в каждом из которых событие A наступает с вероятностью 0,3. Событие B наступает с вероятностью равной 1, если событие произошло не менее двух раз; не может наступить, если событие A не имело место; и наступит с вероятностью 0,6,если событие A имело место один раз. Определить вероятность появления события B. Ответ: 1–(0,74+ 40,730,30,4). Решение: 4 опыта в каждом Р(А)=0,3.
16. Трое шпионов ищут секретную информацию о новейших научных разработках: микрочипах и новых антивирусных программах. Причем первый и второй шпион находят информацию о микрочипах с вероятностью 0,9, а третий– с вероятностью 0,8. Один из этих шпионов получил 8 файлов с секретной информацией, среди |
|
Семинар №6 «Схема Бернулли. Полиномиальная схема» (9 из 12) |
Семинар №6 «Схема Бернулли. Полиномиальная схема» (10 из 12) |
|
которых 2 о новых антивирусных программах. Какова вероятность, что среди следующих 8 файлов, полученных тем же неуловимым шпионом, 2 будут о новых антивирусных программах, а 6 о микрочипах. Указание.
Событие A–найдена
информация новейших научных разработках.
Гипотеза Hk–
информация найдена k-м
шпионом.
Решение: Нет решения 17.
При прохождении одного порога байдарка
не получает повреждений с вероятностью
p1, полностью
ломается вероятностью p2,
получает серьезное повреждение с
вероятностью p3
(p1+p2+p3=1).
Два серьезных повреждения приводят
к полной поломке. Найти вероятность
того, что при прохождении n
порогов байдарка не будет полностью
сломана. Ответ:
Решение: Схема Бернулли: n испытаний. Необходимо,
чтобы событие
Или событие
18. Пусть n,i–число появлений исхода i в первых испытаниях в полиномиальной схеме (см введение). Найти а) P{n,1=d1}; б) P{n,2=d2,…, n,m=dm| n,1=d1}. Указание. а) Решить двумя способами. 1) Воспользоваться формулой
|
2) Положить Решение: 1)Возможных
способов разместить
При этом
должно произойти
Р= 2) Имеем для
происхождения событий 1,2,…,к (из m
вариантов)
(
Если
|
|
Семинар №6 «Схема Бернулли. Полиномиальная схема» (11 из 10) |
Семинар №6 «Схема Бернулли. Полиномиальная схема» (12 из 12) |
|
19. Игральную кость бросают до тех пор, пока впервые не выпадет меньше 5 очков. Какова вероятность получить на последнем бросании не меньше двух очков? Указание.
Пусть n–число
выпавших очков при n-м
бросании. Положим An={n5},
Bn={2n<5}.
Решить двумя способами. 1) Показать,
что событие C, вероятность
которого требуется найти, можно
представить в виде
Решение: Имеем : если
бросание последнее, то выпало
Необходимо,
чтобы выпало
Получаем:
Р(А)= 20. Испытание в полиномиальной схеме с исходами 1, 2, 3, имеющими вероятности p1, p2, p3 соответственно, заканчиваются, когда впервые не появится исход 3. Найти вероятность того, что испытания закончатся исходом 1. Ответ: p1/(p1+p2). Решение:
Р(А)=Р( 21.
(Задача Банаха). Для прикуривания
гражданин пользовался двумя коробками
спичек, доставая случайно ту или иную
коробку. Через некоторое время он
обнаружил, что одна коробка пуста.
Какова вероятность, что во второй
коробке при этом k
спичек, если вначале в каждой коробке
было по n спичек?
Ответ: Решение: Осталось к спичек => было проведено 2n-k испытаний(прикурив) |
Необходимо, чтобы произошло n «успехов» и (n-k) «неуспехов»: Р= 22.
Движением частицы по целым точкам
прямой управляет схема Бернулли с
вероятностью p исхода
1: если в данном испытании схемы Бернулли
появилась 1, то частица из своего
положения переходит в правую соседнюю
точку, а в противном случае – в левую.
Найти вероятность того, что частица
за n шагов из точки
0 перейдет в точку m.
Указание. Число единиц в n
испытаниях однозначно определяет
положение частицы. Ответ: Решение: Если в n испытаниях выпало к единиц, то частица сдвинется по оси х на (n-k) влево и на к вправо => х(к)=-(n-k)+k=-n+2k; m=-n+2k=>
k= В этом случае
к Получаем: по формуле полиномиальной схемы: Р=
|

 ,
1–
,
1– .
.
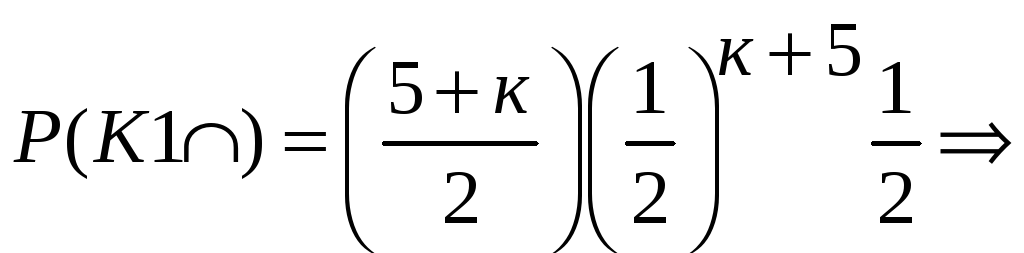 аналогично
аналогично
 ;
;


 ;
б)
;
б)
 .
.


 ;
;