16. Basis in the geometric space (plane and line). The coordinates of a vector in a basis.
A basis on a line is any non-zero vector belonging to this line. A basis on a plane is any pair of linearly independent vectors belonging to the plane. A basis on space is any triple of linearly independent vectors.
A basis is orthogonal if the vectors forming the basis are pairwise orthogonal (mutually perpendicular). An orthogonal basis is orthonormal if the vectors forming the basis have the length 1.
A
spatial basis composed of linearly independent vectors
is denoted by
.
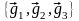An orthogonal or orthonormal basis is denoted by
.
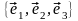Theorem.
Let
be a basis. Then every vector
in the space can be uniquely represented as
where
are some numbers.
Theorem.
Two vectors
and
on
plane are linearly dependent iff their coordinates in some basis
satisfy the condition
.
Proof.
()
Let
and
be linearly dependent. Then
or in coordinate form
.
Excluding
from these two scalar equalities, we have
,
i.e.
.
()
Let
.
Then we have
for
and
,
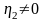i.e. the corresponding coordinates of vectors
and
are proportional and consequently
and
are linearly dependent. The case
is proposed to consider yourself.
Theorem.
Three vectors
,
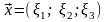and
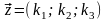in space are linearly dependent iff their coordinates in some basis
satisfy the condition
.
Corollary. The equalities and are necessary and sufficient conditions of collinearity of a pair of vectors on plane and coplanarity of a triple of vectors in space respectively.
17. Cartesian system of coordinates. Radius-vector of a point. Finding the coordinates of a point dividing a segment in some ratio.
The
set consisting of a basis
and a point O
in which are put the beginnings of all basis vectors is called a
common
Cartesian system of coordinates
and is denoted by
.
A system of coordinates
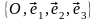generated by an orthonormal basis
is called rectangular
(or orthonormal)
system of coordinates. If a system of coordinates
is given, then for an arbitrary point M
in space can be put in one-to-one correspondence the vector
of
which the beginning is in O
and the end – in M.
Vector
is called the radius-vector
of M
in the system of coordinates
.
The coordinates of the radius-vector of M are called the coordinates
of
M
in the system of coordinates
.
Let
the coordinates of non-coinciding points M1
and M2
in some common Cartesian system of coordinates
with
and
be given. Find the point M such that
.
Solution:
.
Since
,
we have
.
Consequently,
.
23. Fundamental system of solutions of a homogeneous system of equations. Subspaces formed by solutions of a homogeneous linear system of equations.
Consider a homogeneous linear system of equations
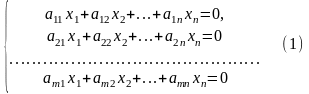
Let
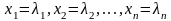be a solution of the system. Write this solution as the vector
The collection of linearly independent solutions
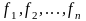of the system of equations (1) is called the fundamental
system of solutions
if any solution of the system of equations (1) can be represented in
form of linear combination of vectors
.
Theorem (on existence of fundamental system of solutions). If the rank of the matrix
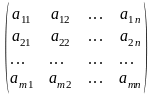
is less than n then the system (1) has non-zero solutions. The number of vectors determining the fundamental system of solutions is found by the formula k = n – r where r is the rank of the matrix.
Thus, if we consider the linear space Rn of which vectors are all possible systems of n real numbers then the collection of all solutions of the system (1) is a subspace of the space Rn. The dimension of this subspace is equal to k.