25)Представление отношений в эвм, матрица отношения.

Удобным способом представления отношений в ЭВМ является матричная форма. Рассмотрим два конечных множества A={a₁,a₂,…,a_m}, B={b₁,b₂,…,b_n} и бинарное отношение P AB . Определим матрицу [P] = (p_ij) бинарного отношения P по следующему правилу:   Полученная матрица содержит полную информацию о связях между элементами и позволяет представлять эту информацию на компьютере.

 Заметим, что любая матрица, состоящая из нулей и единиц, является матрицей некоторого бинарного отношения.

П ример 1.16 Рассмотрим отношение P на множестве A², где A={1,2,3} (см. иллюстрацию).  Матрица этого отношения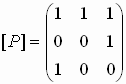 

 

Основные свойства матриц бинарных отношений:

1. Если бинарные отношения P,Q AB, [P] =(p_ij), [Q] = (q_ij), то [P Q] = (p_ij+q_ij), [P Q] = (p_ij·q_ij), где умножение осуществляется обычным образом, а сложение – по логическим формулам (т.е. 0+0=0, во всех остальных случаях 1). Итак: [P Q] = [P]+[Q], [P Q] = [P]*[Q].

Пример 1.17 Пусть отношения P и Q заданы:  . Тогда матрица их суммы [P Q] = [P]+[Q] =  ,  матрица произведения: [P Q] = [P]*[Q] =  .

2. Если бинарные отношения P  A´ B, Q  BC, то [P◦Q] = [P]·[Q] , где умножение матриц [P] и [Q] осуществляется по обычному правилу, а произведение и сумма элементов из [P] и [Q] – по правилам пункта 1.

3. Матрица обратного отношения P^–1 равна транспонированной матрице отношения P: [P^–1]=[P]^T.

4. Если PQ, [P]=(p_ij), [Q]=(q_ij), то p_ij q_ij.  i,j.

5. Матрица тождественного отношения единична: [I_A] = (I_ij) :  I_ij =1  i=j.

6. Пусть R – бинарное отношение на A². Отношение R называется рефлексивным, если  xA (x,x) R, т.е. I_AR (на главной диагонали R стоят единицы). Отношение R называется симметричным, если x,yA (x,y)R  (y,x)R, т.е. R^–1=R, или [R]=[R]^T (матрица симметрична относительно главной диагонали). Отношение R называется антисимметричным, если R  R^–1 I_A, т.е. в матрице [R  R^–1]=[R]*[R]^T вне главной диагонали все элементы равны 0. Отношение R наз. транзитивным, если (x,y)R, (y,z)R (x,z)R, т.е. R◦R R.

Пример 1.18 Пусть отношение P на множестве A², где A={1,2,3}, задано матрицей  .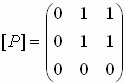

Поскольку на главной диагонали есть нулевые элементы, отношение не рефлексивно. Поскольку матрица не симметрична, отношение тоже не является симметричным. Проверим его антисимметричность, для чего возьмем транспонированную матрицу и вычислим

[PP^-1] = [P]*[P]^T = . Все элементы вне главной диагонали равны 0,  отношение антисимметрично. Проверим транзитивность по матрице: выполняется ли [P◦P]   [P]? [P◦P] =    отношение транзитивно.