2. Цепи переменного тока. Символический метод расчета

 

В общем виде цепи, содержащие   и   описываются системой интегродифференциальных уравнений (см. пример 2). Однако в важном для практики случае сигналов гармонической формы   система сводится к тригонометрическим функциям. Определим напряжения на элементах  ,  ,  . . , где   - индуктивное сопротивление. , где   - емкостное сопротивление.

Из полученных выражений видно, что напряжение на  совпадает с током по фазе, на   опережает ток на  , а на  отстает на  . Определим напряжение на ветви с  .  

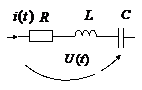
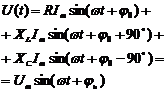      (1)

 

Для определения  и   воспользуемся векторным представлением суммы синусоидальных функций. Векторы напряжений откладываются для действующих значений  (см. также стр. 32):

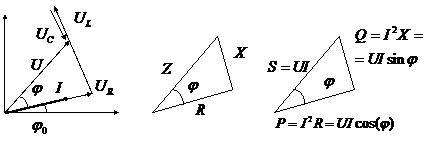Из графических построений видно: ;  - угол сдвига между током и напряжением. Разделив все стороны треугольника напряжений на  , получим подобный ему треугольник сопротивлений, где  - активное сопротивление;  - реактивное сопротивление ветви;  - полное сопротивление ветви. Если умножить все стороны треугольника напряжений на ток  , то получим треугольник мощностей, где  [Вт] – активная мощность;           [ВАр] – реактивная мощность;  [ВА]  - полная мощность. В расчетах более сложных схем использование векторных диаграмм затруднительно. Для анализа электрических схем предложен более изящный метод применения комплексных чисел.

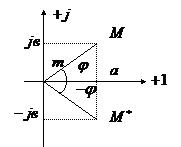; ;    (комплексносопряженное) .

 

При сложении, вычитании удобна алгебраическая форма представления комплексного числа:  . При умножении, делении, возведении в степень более удобна показательная форма: . Для проведения расчетов понадобятся формулы перехода от одной формы к другой: от показательной к алгебраической:    от алгебраической к показательной:             ( , если а<0).

Рассмотрим комплексную функцию  Между ней и вещественной функцией   есть соответствие, т.е. зная одну из них, можно восстановить другую. Оригинал  изображение. Запишем выражение (1) для изображений: Разделив все части члены на  , перейдем от комплексных функций к комплексным числам:   или  , где                                                                    (2)    - комплекс действующего значения тока;  - комплекс действующего значения напряжения. Выражение (2) можно записать более компактно: , где                                                          (3)  - комплексное сопротивление. По выражениям (2) и (3) можно соответственно представить комплексные схемы замещения ветви с  :

 

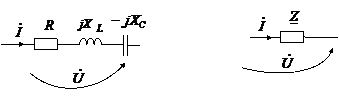
Итак, для определения   для ветви с   следует вначале представить комплексную схему замещения. Далее определить по оригиналу тока его комплекс и рассчитать комплексное сопротивление:

,           . Затем по закону Ома находится комплекс напряжения:  . По найденному   восстанавливается искомое напряжение:

. Аналогичный алгоритм поиска токов для схемы примера 2. На основании исходной схемы сразу же приводится комплексная схема замещения (вначале развернутая, затем компактная):

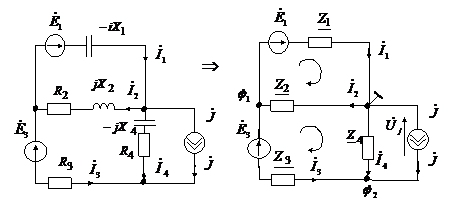
По законам Кирхгофа составляем уравнения: 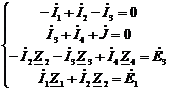     , где известны:

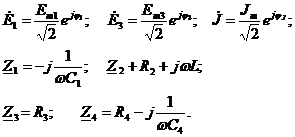Найти:  . Запишем систему уравнений в матричном виде:

 

,     или    . Для определения вектора искомых токов   умножим уравнение слева и справа на  . Получим  . После определения комплексов искомых токов восстанавливаются мгновенные значения токов (оригиналы), например:            и т.д. Для записи баланса мощности в комплексном виде, рассмотрим вначале ветвь  :   , т.е. запись   сразу учитывает активную и реактивную мощности потребителя. Для нашего примера баланс мощности записывается:      или    .    Закон Ома в комплексной форме:  .  

Соединение звездой:

       Если фазные обмотки генератора или потребителя соединить так, чтобы концы обмоток были соединены в одну общую точку, а начала обмоток присоединены к линейным проводам, то такое соединение называется соединением звездой и обозначается условным знаком Y. На рис. 1 обмотки генератора и потребителя соединены звездой. Точки, в которых соединены концы фазных обмоток генератора или потребителя, называются соответственно нулевыми точками генератора (0) и потребителя (0’). Обе точки 0 и 0’ соединены проводом, который называется нулевым, или нейтральным проводом. Остальные три провода трехфазной системы, идущие от генератора к потребителю, называются линейными проводами. Таким образом, генератор соединен с потребителем четырьмя проводами. Поэтому эта система называется четырехпроводной системой трехфазного тока.

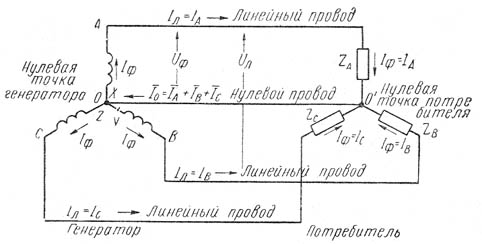
Рис. 1. Соединение звездой

    Сравнивая несвязанную и четырехпроводную системы трехфазного тока, видим, что в первом случае роль обратного провода выполняют три провода системы, а во втором – один нулевой провод. По нулевому проводу протекает ток, равный геометрической сумме токов:

IA, IB и IC, т. е. Ī0= ĪA + ĪB + ĪC.       Напряжения, измеренные между началами фаз генератора (или потребителя) и нулевой точкой (или нулевым проводом), называются фазными напряжениями и обозначаются UA, UB и UC, или в общем виде Uф. Часто задаются величины э.д.с. фазных обмоток генератора. Они обозначаются ЕA, ЕB и ЕC, или Еф. Если пренебречь сопротивлениями обмоток генератора, то можно записать:  ЕA= UA, ЕВ= UВ, ЕC= UС.       Напряжения, измеренные между началами двух фаз: А и В, В и С, С и А – генератора или потребителя, называются линейными напряжениями и обозначаются UАВ, UВС, UСА, или в общем виде Uл. На рис. 1 стрелки показывают выбранное положительное направление тока, которое в линейных проводах принято от генератора к потребителю, а в нулевом проводе – от потребителя к генератору.       Если присоединить зажимы вольтметра к точкам А и В, то он покажет линейное напряжение UАВ. Так как положительные направления фазных напряжений UA, UB и UC выбраны от начал фазных обмоток к их концам, то вектор линейного напряжения UАВ будет равен геометрической разности векторов фазных напряжений UA и UB: ŪAВ=ŪA— ŪВ.      Аналогично можно записать:  ŪВС=ŪВ— ŪС;

ŪСА=ŪС— ŪА.     Иначе можно сказать, что мгновенное значение линейного напряжения равно разности мгновенных значений соответствующих фазных напряжений. На рис. 2 вычитание векторов заменено сложением векторов:  UA и — UB; UВ и — UС; UС и — UА.     Из векторной диаграммы видно, что векторы линейных напряжений составляют замкнутый треугольник.

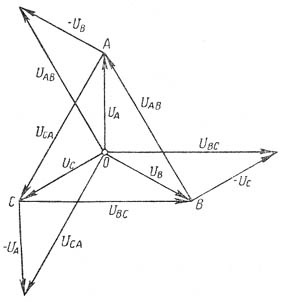
Рис. 2. Фазные и линейные напряжения при соединении звездой

Зависимость между линейным и фазным напряжениями:  UBС=2UBcos30o, так как cos30o=√3/2, то UBС=√3UB, или в общем виде Uл=√3Uф.     Следовательно, при соединении звездой линейное напряжение в √3 раз больше фазного напряжения.      Ток, протекающий по фазной обмотке генератора или потребителя, называется фазным током и обозначается в общем виде Iф. Ток, протекающий по линейному проводу, называется линейным током и обозначается в общем виде Iл. На рис. 1 видно, что при соединении звездой линейный ток равен фазному току, т. е.  Iл=Iф.      Рассмотрим случай, когда нагрузка в фазах потребителя одинакова как по величине, так и по характеру. Такая нагрузка называется равномерной, или симметричной. Это условие выражается равенством. z1= z2= z3.      Нагрузка не будет равномерной, если, например, z1= r1=0,5ом; z2=ωL2=0,5ом и z3=1/ωC3=0,5ом, так как здесь выполнено лишь одно условие – равенство сопротивлений фаз потребителя по величине, в то время как характер сопротивлений различен (r1 - активное сопротивление, ωL2 - индуктивное сопротивление, 1/ωC3 - емкостное сопротивление).       При симметричной нагрузке: IА=UА/zА; IВ=UВ/zВ; IС=UС/zС; IА=IВ=IС.    Фазные коэффициенты мощности вследствие равенства сопротивлений и одинаковости их характера будут одинаковы:  cosφ1=rА/zА; cosφ2=rB/zB; cosφ3=rC/zC; cosφ1=cosφ2=cosφ3.     В нулевом проводе должна протекать геометрическая сумма токов всех трех фаз. Если посмотреть на кривые изменения токов при симметричной нагрузке трехфазной системы, то увидим, что максимальные значения для всех трех синусоид тока одинаковы. Поскольку при симметричной нагрузке сумма мгновенных значений токов трехфазной системы равна нулю, следовательно, ток в нулевом проводе будет равен нулю.     Отбрасывая нулевой провод в четырехпроводной системе, переходим к трехпроводной системе трехфазного тока. Если имеется симметричная нагрузка, как, например, трехфазные двигатели переменного тока, трехфазного тока, трехфазные печи, трехфазные трансформаторы и т. п., то к такой нагрузке подводятся только три провода. Потребители, включенные звездой с несимметричной нагрузкой фаз, нуждаются в нулевом проводе.      При симметричной нагрузке фазные напряжения отдельных фаз равны между собой. При несимметричной нагрузке трехфазной системы симметрия токов и напряжений нарушается. Однако в четырехпроводных цепях часто пренебрегают незначительной несимметрией фазных напряжений. В этих случаях между линейными и фазными напряжениями существует зависимость:

  Uл=√3Uф.

Соединение треугольником:

      Кроме соединения звездой, генераторы, трансформаторы, двигатели и другие потребители трехфазного тока могут включаться треугольником.      Если объединить попарно провода несвязанной шестипроводной системы и соединить фазы, как показано на рисунке 1, получим трехфазную трехпроводную систему, соединенную треугольником.

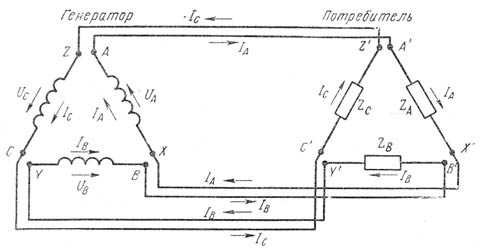
Рис. 1. Несвязанная трехфазная схема.

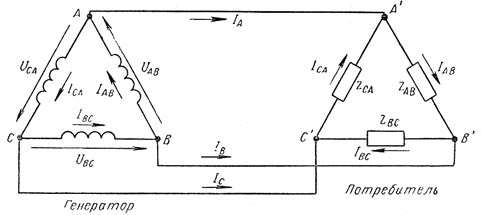
Рис. 2. Связанная трехфазная схема, соединенная треугольником.

      Соединение треугольником выполняется таким образом (рис. 2), чтобы конец фазы А был соединен с началом фазы В, конец фазы В соединен с началом фазы С и конец фазы С соединен с началом фазы А. К местам соединения фаз присоединяют линейные провода. Если обмотки генератора соединены треугольником, то линейное напряжение создает каждая линейная обмотка. У потребителя, соединенного треугольником, линейное напряжение подключается к зажимам фазного сопротивления. Следовательно, при соединении треугольником фазное напряжение равно линейному: Uл=Uф.        Определим зависимость между фазными и линейными токами при соединении треугольником, если нагрузка фаз будет одинакова по величине и характеру. Составляем уравнения токов по первому закону Кирхгофа для трех узловых точек А1, B1 и C1 потребителя: ĪA+ ĪСА= ĪАВ; ĪВ+ ĪАВ= ĪВС; ĪС+ ĪВС= ĪСА; откуда ĪA= ĪАВ—ĪСА; ĪВ= ĪВС—ĪАВ;  ĪС= ĪСА—ĪВС.       Отсюда видно, что линейные токи равны геометрической разности фазных токов. При симметричной нагрузке фазные токи одинаковы по величине и сдвинуты один относительно другого на 120o. Производя вычитание векторов фазных токов согласно полученным уравнениям, получаем линейные токи. Зависимость между фазными и линейными токами при соединении в треугольник:  Iл=2Iфcos30o=2Iф√3/2=√3Iф.     Следовательно, при симметричной нагрузке, соединенной треугольником, линейный ток в √3 раз больше фазного тока.       У двигателей и у других потребителей трехфазного тока в большинстве случаев наружу выводят все шесть концов обмоток, которые по желанию можно соединять либо звездой, либо треугольником. Обычно к трехфазной машине крепится доска из изоляционного материала (клеммная доска), на которую и выводят все шесть концов.         Если у нас есть двигатель, на паспорте которого написано 127/220 в, значит, этот двигатель можно использовать на два напряжения 127 и 220 в.      Если линейное напряжение сети равно 127 в, то обмотки двигателя необходимо включить треугольником. Тогда на обмотку каждой фазы двигателя будет подано напряжение 127 в. При напряжении 220 в обмотки двигателя нужно включить звездой, тогда обмотка каждой фазы также будет под напряжением 127 в.