
- •26. Взаимоиндукция
- •27. Электрическая емкость. Конденсаторы
- •28. Переменный ток
- •29. Способы изображения синусоидальных величин
- •1. Графическое изображение синусоидальных величин.
- •2. Векторное изображение синусоидальных величин.
- •3. Представление синусоидальных величин комплексными числами.
- •30. Сложение синусоидальных величин
- •32. Cреднее значение переменного тока
- •34. Цепь переменного тока с индуктивностью
- •35. Цепь переменного тока, содержащая емкость
- •2. Цепи переменного тока. Символический метод расчета
- •Переходные процессы в электрических цепях
- •Переходные процессы при отключении катушки индуктивности
- •Переходные процессы при замыкании катушки индуктивности
- •Переходные процессы при разрядке конденсатора через резистор
Взаимодействие точечных заряженных тел описывается законом Кулона.
Сила взаимодействия F между точечными заряженными телами Q и q, расположенными в данной среде на расстоянии R друг от друга, прямо пропорциональна произведению зарядов этих тел и обратно пропорциональна квадрату расстояния между ними:
F = Qq/(4πεrεoR2) ,
где Q и q — значения зарядов, Кл (1 Кл = 6,3*1018 зарядов электрона); εг — относительная диэлектрическая проницаемость среды, показывающая, во сколько раз сила взаимодействия в данной среде меньше, чем в вакууме (величина безразмерная); εо=8,86*10-12 Ф/м — электрическая постоянная.
Введем силовую характеристику поля — напряженность:
E=F/q.
Напряженность электрического поля в данной точке определяется силой, действующей на помещенное в эту точку пробное тело, обладающее единичным положительным зарядом.
Единица напряженности
[E] = Н/Кл (ньютон на кулон).
Для поля уединенного точечного заряженного тела на основании закона Кулона
E=Q/(4πεrεoR2).
Рассмотрим в качестве примера электрическое поле уединенного заряженного металлического шара с зарядом -Q.Напряженность электрического поля внутри металлического шара при статическом заряде равна нулю. В самом деле, при наличии электрического поля в проводящей среде электроны благодаря взаимному отталкиванию придут в движение и, следовательно, статическое состояние установится только тогда, когда напряженность поля внутри шара станет равной нулю. Таким образом, избыточный электрический заряд распределится только на его поверхности.
Напряженность поля вне шара и на его поверхности находят, предполагая, что заряд -Q сосредоточен в центре шара.
2. Электрический потенциал. Электрическое поле обладает определенным запасом энергии, т. е. способностью совершать работу. Как известно, энергию можно также накопить в пружине, для чего ее нужно сжать или растянуть. За счет этой энергии можно получить определенную работу. Если освободить один из концов пружины, то он сможет переместить на некоторое расстояние связанное с этим концом тело. Точно так же энергия электрического поля может быть реализована, если внести в него какой-либо заряд. Под действием сил поля этот заряд будет перемещаться по направлению силовых линий, совершая определенную работу. Для характеристики энергии, запасенной в каждой точке электрического поля, введено специальное понятие — электрический потенциал. Электрический потенциал ? поля в данной точке равен работе, которую могут совершить силы этого поля при перемещении единицы положительного заряда из этой точки за пределы поля. Понятие электрического потенциала аналогично понятию уровня для различных точек земной поверхности. Очевидно, что для подъема локомотива в точку Б (рис. 7) нужно затратить большую работу, чем для подъема его в точку А. Поэтому локомотив, поднятый на уровень Н2, при спуске сможет совершить большую работу, чем локомотив, поднятый на уровень Н2 За нулевой уровень, от которого производится отсчет высоты, принимают обычно уровень моря.
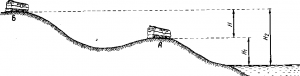 Рис.
7. Разность уровней в поле земного
тяготения
Рис.
7. Разность уровней в поле земного
тяготения
 Рис.
8. Разность потенциалов U между точками
А и Б электрического поля определяет
работу, которая затрачивается на
перемещение заряда q между этими точками
Рис.
8. Разность потенциалов U между точками
А и Б электрического поля определяет
работу, которая затрачивается на
перемещение заряда q между этими точками
Точно так же за нулевой потенциал условно принимают потенциал, который имеет поверхность земли. Электрическое напряжение. Различные точки электрического поля обладают разными потенциалами. Обычно нас мало интересует абсолютная величина потенциалов отдельных точек электрического поля, но нам весьма важно знать разность потенциалов ?1—?2 между двумя точками поля А и Б (рис. 8). Разность потенциалов ?1 и ?2 двух точек поля характеризует собой работу, затрачиваемую силами поля на перемещение единичного заряда из одной точки поля с большим потенциалом в другую точку с меньшим потенциалом. Точно так же нас на практике мало интересуют абсолютные высоты Н1и Н2 точек А и Б над уровнем моря (см. рис. 7), но для нас важно знать разность уровней И между этими точками, так как на подъем локомотива из точки А в точку Б надо затратить работу, зависящую от величины Я. Разность потенциалов между двумя точками поля носит название электрического напряжения. Электрическое напряжение обозначают буквой U (и). Оно численно равно отношению работы W, которую нужно затратить на перемещение положительного заряда q из одной точки поля в другую, к этому заряду, т. е.
U = W / q (2)
Следовательно, напряжение U, действующее между различными точками электрического поля, характеризует запасенную в этом поле энергию, которая может быть отдана путем перемещения между этими точками электрических зарядов. Электрическое напряжение — важнейшая электрическая величина, позволяющая вычислять работу и мощность, развиваемую при перемещении зарядов в электрическом поле. Единицей электрического напряжения служит вольт (В). В технике напряжение иногда измеряют в тысячных долях вольта — милливольтах (мВ) и миллионных долях вольта — микровольтах (мкВ). Для измерения высоких напряжений пользуются более крупными единицами — киловольтами (кВ) — тысячами вольт. Напряженность электрического поля при однородном поле представляет собой отношение электрического напряжения, действующего между двумя точками поля, к расстоянию l между этими точками:
E = U / l (3)
Напряженность электрического поля измеряют в вольтах на метр (В/м). При напряженности поля в 1 В/м на заряд в 1 Кл действует сила, равная 1 ньютону (1 Н). В некоторых случаях применяют более крупные единицы измерения напряженности поля В/см (100 В/м) и В/мм (1000 В/м).
3. Электропроводность
Свойство вещества проводить под действием не изменяющегося во времени электрического поля не изменяющийся во времени электрический ток.
В зависимости от природы токопроводящих частиц и от их
электропроводности все вещества можно условно разделить на пять групп.
1. Непроводящие тела, или изоляторы.
2. Проводники первого рода, или электронопроводящие тела.
3. Полупроводники – вещества, в которых ток переносится электронами
и дырками.
4. Проводники второго рода, или ионные проводники, - вещества, в
которых ток переносится ионами.
5. Смешанные проводники – тела, сочетающие электронную ионную
проводимости.
Мерой способности веществ проводить электрический ток является
электрическая проводимость L – величина, обратная электрическому
сопротивлению R. Так как,
[pic]
то
[pic]
где ? – удельное сопротивление, Ом*м; S – поперечное сечение, м2; 1/?
= – удельная электрическая проводимость.
Удельная электрическая проводимость раствора электролита (Ом-
1*см-1) – это электрическая проводимость объема раствора, заключенного
между двумя параллельными электродами, имеющими площадь 1 м2 и
расположенными на расстоянии 1 м друг от друга.
4. Электрические цепи и их элементы
Электрическая цепь представляет собой совокупность устройств и объектов, образующих путь для электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий об электродвижущей силе, токе и напряжении. В электрической цепи постоянного тока могут действовать как постоянные токи, так и токи, направление которых остается постоянным, а значение изменяется произвольно во времени или по какому-либо закону.
Электрическая цепь состоит из отдельных устройств или элементов, которые по их назначению можно разделить на 3 группы. Первую группу составляют элементы, предназначенные для выработки электроэнергии (источники питания). Вторая группа — элементы, преобразующие электроэнергию в другие виды энергии (механическую, тепловую, световую, химическую и т. д.). Эти элементы называются приемниками электрической энергии (электроприемниками). В третью группу входят элементы, предназначенные для передачи электроэнергии от источника питания к электроприемнику (провода, устройства, обеспечивающие уровень и качество напряжения, и др.).
Источники питания цепи постоянного тока — это гальванические элементы, электрические аккумуляторы, электромеханические генераторы, термоэлектрические генераторы, фотоэлементы и др. Все источники питания имеют внутреннее сопротивление, значение которого невелико по сравнению с сопротивлением других элементов электрической цепи.
Электроприемниками постоянного тока являются электродвигатели, преобразующие электрическую энергию в механическую, нагревательные и осветительные приборы и др. Все электроприемники характеризуются электрическими параметрами, среди которых можно назвать самые основные — напряжение и мощность. Для нормальной работы электроприемника на его зажимах (клеммах) необходимо поддерживать номинальное напряжение. Для приемников постоянного тока оно составляет 27, 110, 220, 440 В, а также 6, 12, 24, 36 В.
Графическое изображение электрической цепи, содержащее условные обозначения ее элементов и показывающее соединения этих элементов, называется схемой электрической цепи. В табл. 2 показаны условные обозначения, применяемые при изображении электрических схем.
Таблица 2. Условные обозначения в электросхемах |
|
Элемент гальванический или
аккумуляторный
|
Контакты замыкающие с выдержкой времени |
Батарея элементов
|
при замыкании
|
Генератор электромеханический
постоянного тока
|
при размыкании
|
Выключатель, контакт замыкающий
|
при замыкании и размыкании
|
Выключатель автоматический
|
Предохранитель плавкий
|
Контакты контактора и электрического реле: |
Обмотка контактора, магнитного
пускателя и реле
|
замыкающие
|
Лампа накаливания осветительная
|
размыкающие
|
|
переключающие
|
|
Лампа газоразрядная осветительная
|
Конденсатор постоянной емкости
|
Амперметр и вольтметр
|
Катушка индуктивности
|
Резистор постоянный
|
Диод полупроводниковый
|
Резистор переменный
|
|
Участок электроцепи, вдоль которого протекает один и тот же ток, называется ветвью. Место соединения ветвей электроцепи называется узлом. На электросхемах узел обозначается точкой. Любой замкнутый путь, проходящий по нескольким ветвям, называется контуром электрической цепи. Простейшая электрическая цепь имеет одноконтурную схему, сложные электрические цепи — несколько контуров.
Элементами электрической цепи являются различные электротехнические устройства, которые могут работать в различных режимах. Режимы работы как отдельных элементов, так и всей электрической цепи характеризуются значениями тока и напряжения. Поскольку ток и напряжение в общем случае могут принимать любые значения, то режимов может быть бесчисленное множество.
Режим холостого хода — это режим, при котором тока в цепи нет. Такая ситуация может возникнуть при разрыве цепи. Номинальный режим бывает, когда источник питания или любой другой элемент цепи работает при значениях тока, напряжения и мощности, указанных в паспорте данного электротехнического устройства. Эти значения соответствуют самым оптимальным условиям работы устройства с точки зрения экономичности, надежности, долговечности и пр.
Режим короткого замыкания — это режим, когда сопротивление приемника равно нулю, что соответствует соединению положительного и отрицательного зажимов источника питания с нулевым сопротивлением. Ток короткого замыкания может достигать больших значений, во много раз превышая номинальный ток. Поэтому режим короткого замыкания для большинства электроустановок является аварийным.
Согласованный режим источника питания и внешней цепи возникает в том случае, когда сопротивление внешней цепи равно внутреннему сопротивлению. В этом случае ток в цепи в 2 раза меньше тока короткого замыкания.
Самыми распространенными и простыми типами соединений в электрической цепи являются последовательное и параллельное соединение.
5. Электродвижущая сила - электрическая разность потенциалов, создаваемая источником электрической энергии (электрохимическим элементом, механическим генератором, термоэлементом, фотоэлементом и пр.).
1. Нагрузкой называют преобразователь электрической энергии в другой ее вид (механическую, химическую, тепловую и т.д.). Нагрузку на электрических схемах принято обозначать буквой R . Единица сопротивления (нагрузки) – ом (Ом). На электрических схемах нагрузку изображают в виде (рис. 1.1).
2. 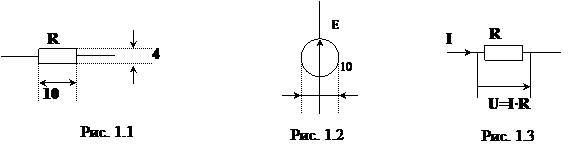
Источником называют преобразователь механической, химической, тепловой и т.д. энергии в электрическую. Источник, генератор на электрических схемах
принято обозначать буквой E. Единица – вольт (В). На электрических схемах его
принято изображать в виде (рис. 1.2).
Источник электродвижущей силы (ЭДС) –
это такой источник, который вырабатывает
постоянную по величине ЭДС (![]() ),
независимо от нагрузки. Такой источник
называют идеальным.
),
независимо от нагрузки. Такой источник
называют идеальным.
Неидеальный (реальный) источник, это
такой источник, у которого внутреннее
сопротивление ![]() не
равно нулю.
не
равно нулю.
3. Напряжение; падение напряжения; разность потенциалов принято на электрических схемах обозначать буквой U . Единица напряжения – вольт (В).
4. Сила электрического тока; электрический ток; ток обозначают буквой I .
Единица тока – ампер (А).
Е сли
по нагрузке R пропустить ток I, то на ней
будет падать напряжение
сли
по нагрузке R пропустить ток I, то на ней
будет падать напряжение![]() .
Это и есть закон Ома для ветви (рис. 1.3).
Закон Ома можно записывать в одной из
следующих форм:
.
Это и есть закон Ома для ветви (рис. 1.3).
Закон Ома можно записывать в одной из
следующих форм:
![]()
Создадим замкнутую цепь (рис. 1.4). Ток в
этой цепи можно определить по закону
Ома для замкнутой ветви: ![]() .
.
5. Электрическая цепь – совокупность соединенных между собой источников и нагрузок, по которым могут протекать
электрические токи.
6. Электрическая схема– графическое изображение электрической цепи на бумаге.
7. Ветвь – участок электрической цепи между двумя узлами, в котором все элементы соединены последовательно.
8. Узел – это точка соединения двух или нескольких ветвей. Узел, объединяющий две ветви называют устранимым, так как он находится внутри новой образованной ветви.
6. Закон Ома
Формулировка закона Ома
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого проводника и обратно пропорциональна его сопротивлению: I = U / R; [A = В / Ом]
Ом установил, что сопротивление прямо пропорционально длине проводника и обратно пропорционально площади его поперечного сечения и зависит от вещества проводника. R = ρl / S, где ρ - удельное сопротивление, l - длина проводника, S - площадь поперечного сечения проводника.
Зако́н О́ма — физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока исопротивлением проводника. Экспериментально установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.
В
своей оригинальной форме он был записан
его автором в виде : ![]() ,
,
Здесь X —
показания гальванометра,
т.е в современных обозначениях сила
тока I, a — величина,
характеризующая свойства источника
тока, постоянная в широких пределах и
не зависящая от величины тока, то есть
в современной терминологии электродвижущая
сила (ЭДС) ![]() , l —
величина, определяемая длиной соединяющих
проводов, чему в современных представлениях
соответствует сопротивление внешней
цепи R и, наконец, b параметр,
характеризующий свойства всей установки,
в котором сейчас можно усмотреть учёт
внутреннего сопротивления источника
тока r[1].
, l —
величина, определяемая длиной соединяющих
проводов, чему в современных представлениях
соответствует сопротивление внешней
цепи R и, наконец, b параметр,
характеризующий свойства всей установки,
в котором сейчас можно усмотреть учёт
внутреннего сопротивления источника
тока r[1].
В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает
Закон Ома для полной цепи:
![]() ,
(2)
,
(2)
где:
— ЭДС источника напряжения(В),
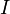 — сила
тока в цепи (А),
— сила
тока в цепи (А),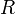 — сопротивление всех
внешних элементов цепи (Ом),
— сопротивление всех
внешних элементов цепи (Ом), — внутреннее
сопротивление источника
напряжения (Ом).
— внутреннее
сопротивление источника
напряжения (Ом).
Из закона Ома для полной цепи вытекают следствия:
При r<<R сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения
При r>>R сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.
Часто[2] выражение:
![]() (3)
(3)
(где ![]() есть напряжение или падение
напряжения, или, что то же, разность
потенциалов между началом
и концом участка проводника) тоже
называют «Законом Ома».
есть напряжение или падение
напряжения, или, что то же, разность
потенциалов между началом
и концом участка проводника) тоже
называют «Законом Ома».
Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:
![]() (4)
(4)
То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.
К другой записи формулы (3), а именно:
![]() (5)
(5)
Применима другая формулировка:
|
Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи. |
|
Выражение (5) можно переписать в виде:
![]() (6)
(6)
где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо[3], впоследствии переименованный в Си́менс (обозначение: См, S).
7.
8. Режимы работы источника ЭДС.
Рассмотрим простую электрическую цепь, состоящую из постоянного источника ЭДС Е с внутренним сопротивлением RВН и приемника энергии с сопротивлением RПР. (рис. 11)
Источник ЭДС Приемник






I


 +
+
Е
U
UПР




RВН UВН



Рис. 11. Электрическая схема для исследования режимов работы источника ЭДС.
ЭДС Е источника является непосредственной причиной возникновения тока I в замкнутой цепи. Допустим, что направление тока I совпадает с направлением ЭДС Е. Направление ЭДС – это направление возрастания потенциала внутри источника ( от – к + ) и обозначается стрелкой внутри него.
Ток в цепи можно определить по закону Ома (здесь и во всех последующих формулах сопротивлением соединительных проводов будем пренебрегать):
![]() ,
(1)
,
(1)
где Е – ЭДС источника – постоянная величина, независящая от режима работы источника; RВН - внутреннее сопротивление источника – так же постоянная величина;
RПР – сопротивление приемника (нагрузки).
Перепишем уравнение (1) в следующем виде:
Е = RВН ∙I + RПР ∙I = UВН + U, (2)
где UВН = RВН ∙I – падение напряжения на внутреннем сопротивлении источника; а U = UПР = RПР ∙I – напряжение на зажимах источника ЭДС равное напряжению на приемнике.
Учитывая выражение (2) найдем напряжение на зажимах источника ЭДС:
U = Е – RВН ∙I = Е – UВН, (3)
U, [В]

1
2
UН

3
UС=E/2

4 [А]

0 IН IС=IКЗ/2 IКЗ I
Рис. 12. Внешняя характеристика источника ЭДС.
Из всех возможных режимов работы источника ЭДС отметим четыре наиболее важные (рис.12):
Точка 1 – холостой ход,
Точка 2 – номинальный режим,
Точка 3 – согласованный режим,
Точка 4 – короткое замыкание.
Проанализируем каждый из перечисленных выше режимов работы источника ЭДС.
Режим холостого хода (т.1) – это режим, при котором сопротивление приемника стремится к бесконечности (RПР = ∞) - на практике это соответствует разрыву электрической цепи, следовательно, ток холостого хода равен нулю (IХ =0). Выражение (3) преобразуется: UХ = Е – RВН∙IХ, (4)
Поскольку на холостом ходу IХ =0 следовательно, напряжение UХ на зажимах источника при пассивной нагрузке будет наибольшим и равным ЭДС Е источника:
UХ = Е
Из опыта холостого хода можно определить ЭДС Е показаниям вольтметра, подключив его непосредственно к разомкнутым зажимам источника ЭДС.
Номинальный режим (т.2) источника характеризуется тем, что напряжение, ток и мощность его соответствуют тем значениям, на которые он рассчитан заводами-изготовителями. При этом гарантируются наилучшие условия работы источника ЭДС (экономичность, долговечность и др.). Величины, определяющие номинальный режим, обычно указывают в паспорте, каталоге или на щитке, прикрепленном к устройству.
При номинальном режиме: UН = Е – RВН∙IН, (5)
Для достижения номинального режима на практике UН должно составлять (0,90,95)E
Согласованный режим (т.3) - это режим, при котором источник отдает в приемник (во внешнюю цепь) максимальную мощность РMAX. Для достижения данного режима работы источника необходимо подобрать величину сопротивления приемника RПР равным внутреннему сопротивлению источника RВН, то есть RПР = RВН (6)
Действительно, мощность, выделяемая в приемнике равна:
![]() ,
где
,
где
![]() ,
(см. формулу 1)
,
(см. формулу 1)
Следовательно,
![]() ;
;
Проведем анализ последней формулы:
Если
RПР = 0, то РПР
=
![]() =0
=0
RПР = ,
то РПР =![]() ,
,
поэтому легко сделать вывод, что РПР имеет экстремум.
Как
известно, положение экстремума любой
функции можно определить из условия:
![]() ,
в нашем случае
,
в нашем случае
![]() ,
следовательно,
,
следовательно,

![]() ,
,
![]() ,
,
![]()
![]()
Таким образом, при согласованном режиме для выделения в приемнике максимальной мощности РПР МАХ, необходимо выполнить условие: RПР = RВН
При согласованном режиме: UС = Е – RВН ∙IС, (7)
Из формулы (7) определим ток, протекающий в цепи при согласованном режиме:
![]() (8)
(8)
Мощность, выделяемая источником равна:
![]() (9)
(9)
а мощность, выделяемая в приемнике:
![]() (10)
(10)
Коэффициент полезного действия (КПД) источника при данном режиме:
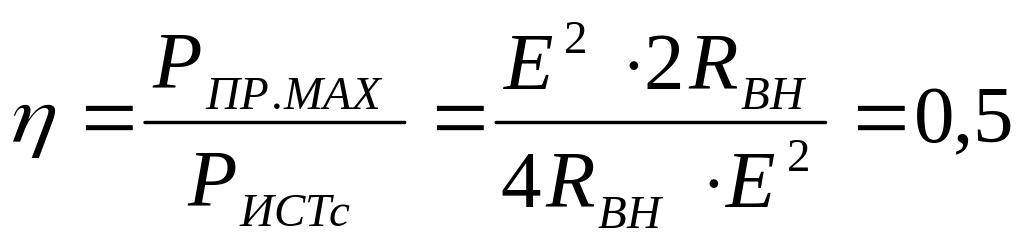 (11)
(11)
Из формулы (11) видно, что 50% энергии источник отдает в приемник, а остальные 50% теряется в самом источнике (на его внутреннем сопротивлении).
Согласованный режим допустим и желателен в системах телемеханики, автоматики, телефонии и т.д., где необходимо выделение в приемнике максимально возможной мощности РПР МАХ, 50% потерями в источнике можно пренебречь, так как такие системы потребляют малую мощность - порядка нескольких Ватт.
Для систем электроснабжения такой режим невозможен, потому что мощности источников энергии исчисляются мегаВаттами (МВт) и 50% потери в источниках будут чрезмерно велики.
Режим короткого замыкания (т.4) характеризуется тем, что сопротивление приемника становится равным нулю RПР = 0. Как правило, на практике это связано с перемыканием приемника электрической энергии проводником с очень малым сопротивлением (RПРОВОД = 0) – так называемое промышленное короткое замыкание, зачастую вызванное неправильной эксплуатацией электротехнических устройств, как например, электрические двигатели, трансформаторы, бытовая техника и т.д.
При RПР = 0 формула (3) трансформируется в следующее выражение:
0 = Е – RВН ∙IКЗ , (12)
так как UКЗ = RПР ∙IКЗ = 0 ∙IКЗ = 0
Как
следует из выражения (12) ток короткого
замыкания равен:
![]() (13)
(13)
Анализируя выражение (13), можно сделать следующий вывод: при Е = const (см. формулу 1) ток короткого замыкания (IКЗ) может достигать очень больших величин из-за малого внутреннего сопротивления источника ЭДС, значительно превышающего номинальные токи (IКЗ >> IН), поэтому режим короткого замыкания, как правило, является очень опасным и нежелательным режимом как для источника, так и для приемника. Однако в некоторых случаях режим короткого замыкания является номинальным для таких электротехнических устройств, как например, сварочные трансформаторы и генераторы, трансформаторы тока и др.
Действительно, современные источники ЭДС изготавливают с достаточно малыми внутренними сопротивлениями RВН. В идеальном случае RВН = 0, следовательно, U = E - 0∙I = E, т.е. напряжение на зажимах такого источника не зависит от величины нагрузки (рис. 13, прямая а) и его называют идеальным источником ЭДС.
 U, [В]
U, [В]


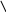


 E
E
1
U'ВН
U''ВН
> U'ВН


 а
а
2


 в
в
U'
U''< U'
 с
с
[A]

0 IНАГР I''КЗ I'КЗ I
Рис. 13. Внешние характеристики источников ЭДС Е.
а – для идеального источника ЭДС с RВН = 0;
в – для реального источника ЭДС с R'ВН 0;
с – для реального источника ЭДС с R''ВН > R'ВН.
На рис. 13 показаны три внешние характеристики источников постоянной ЭДС Е с различными внутренними сопротивлениями RВН. Анализируя кривые а, в и с следует отметить, что в большинстве случаев предпочтительно иметь источник с внешней характеристикой – прямая а, затем прямая в и наихудший вариант – прямая с. Это объясняется тем, что чем больше падение напряжения внутри источника UВН, тем меньше напряжение на его зажимах (см. формулу 3 и рис. 13), а именно U = Е > U' > U'', при условии, что во всех трех случаях ток нагрузки IНАГР (что соответствует суммарной потребляемой мощности приемников) одинаковый.
Согласно ГОСТа 721-77 напряжение на источниках постоянной ЭДС Е и на приемниках должно быть строго регламентировано (установлен номинальный ряд). Так, для источников постоянной ЭДС Е этот ряд: UН = 115 В, 230 В, 460 В и т.д., а для приемников на 5% ниже, что соответствует UН = 110 В, 220 В, 440 В и т.д.
При питании приемников таким напряжением, завод-изготовитель гарантирует наилучшие условия их работы (экономичность, долговечность и др.).
Если считать, что точка 1 прямой в соответствует номинальному напряжению приемников U', то при подключении тех же приемников к источнику с внешней характеристикой – прямая с, напряжение на приемниках становится ниже номинального U'' < U' - точка 2. Это приводит к нарушению нормальной работы приемника, например, если в качестве приемников взять электрические лампочки или обогревательные приборы, то они будут работать в полнакала.
Из опытов холостого хода и короткого замыкания можно определить экспериментальным путем используя формулу (13) внутреннее сопротивление источника ЭДС Е:
![]() (14)
(14)
где Е – определяется по показанию вольтметра из опыта холостого хода, а IКЗ –по показанию амперметра из опыта короткого замыкания.
9.
10. Последовательное соединение – соединение, при котором конец первого проводника соединяют с началом второго, конец второго – с началом третьего и т.д.
Учитель демонстрирует опыты с цепью с последовательно соединёнными лампочками.
Учащиеся делают выводы:
сила тока в цепи при последовательном соединении проводников в любых частях цепи одинакова: I = I1 = I2
общее напряжение в цепи равно сумме напряжений на каждом участке: U = U1 + U2
Обсуждается вопрос: Чему рано общее сопротивление цепи при последовательном соединении проводников?
С помощью закономерностей и закона Ома для участка цепи выводится формула для общего сопротивления проводников: R = R1 + R2.
Обсуждается вопрос: Как найти сопротивление n последовательно соединённых одинаковых проводников? R = nR1
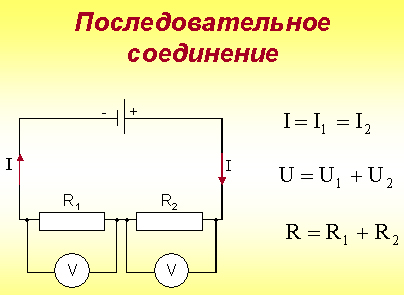
Обсуждается параллельное соединение проводников.
Параллельное соединение – соединение, при котором начала всех проводников присоединяются к одной точке цепи, а их концы к другой.
Учитель демонстрирует опыты с цепью с параллельно соединёнными лампочками.
Учащиеся делают выводы:
cила тока в неразветвлённой цепи равна сумме токов в разветвлениях: I = I1 + I2
yапряжение на каждом из параллельно соединённых проводников одинаково: U = U1 = U2
Обсуждается вопрос: Чему рано общее сопротивление цепи при параллельном соединении проводников?
С
помощью закономерностей и закона Ома
для участка цепи выводится формула для
общего сопротивления проводников: ![]() ,
, ![]() .
.
Обсуждается
вопрос: Как найти сопротивление n
параллельно соединённых одинаковых
проводников? R = ![]()
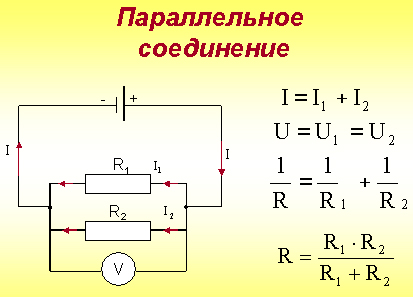
Преимущества и недостатки соединений.
Пример последовательного соединения: гирлянда.
Пример параллельного соединения: потребители в жилых помещениях.
Преимущества и недостатки соединений:
Последовательное – защита цепей от перегрузок: при увеличении силы тока выходит из строя предохранитель, и цепь автоматически отключается. При выходе из строя одного из элементов соединения отключаются и остальные.
Параллельное – при выходе из строя одного из элементов соединения, остальные действуют. При включении элемента с меньшим возможным напряжением в цепь элемент перегорит.
Учащиеся заполняют таблицу в тетради с помощью слайда презентации:
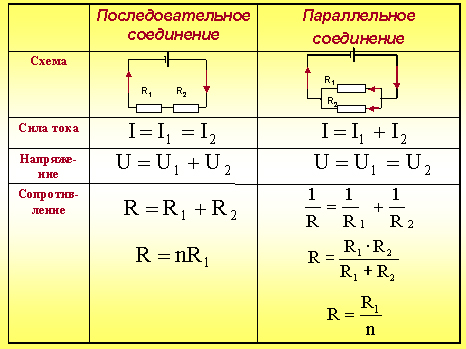
11. Первый закон Кирхгофа
Рассматривая разветвленные электрические цепи, состоящие из нескольких контуров, нам необходимо установить соотношения между токами, приходящими к любому узлу, и токами, уходящими от него. Из физической сущности электрического тока следует, что общее количество носителей тока, притекающее к узлу в течении некоторого промежутка времени, равно количеству носителей, утекающему от узла за тоже время. Если предположить, что это положение не выполняется, то в узловой точке должно происходить накопление зарядов или убыль - утечка зарядов.
На практике эти явления не наблюдаются, следовательно, мы можем утверждать, что сумма величин токов, притекающих к точке разветвления, равна сумме величин токов, утекающих от нее.
Это положение и является формулировкой первого закона Кирхгофа.
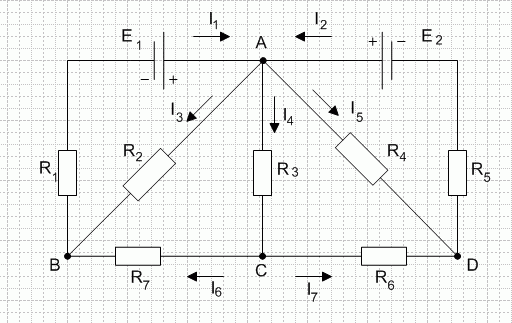
Математическое выражение первого закона Кирхгофа применительно к узлу А:
![]()
откуда
![]()
Условимся токи, притекающие к точке разветвления, считать положительными, а токи, утекающие от нее, - отрицательными и сформулируем окончательно первый закон Кирхгофа:
Алгебраическая сумма величин токов в точке разветвления равна нулю.
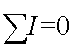
Пример
На рисунке изображена узловая точка и указаны направления и величины в пяти ветвях.
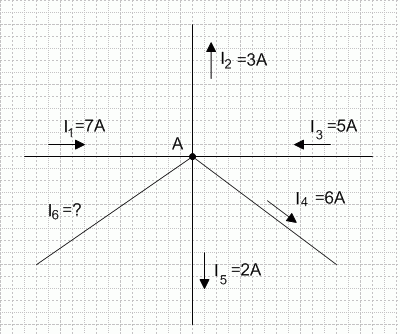
Требуется определить величину и направление тока в шестой ветви.
Решение.
Предположим, что ток в шестой ветви притекает к точке А. Используя первый закон Кирхгофа, составим уравнение ∑I=0

Отсюда
![]()
![]()
![]()
![]()
Знак минус означает, что принятое нами направление тока в шестой ветви неправильное, В действительности ток в этой ветви вытекает из точки А.
Второй закон Кирхгофа
Второй закон Кирхгофа связывает между собой э. д. с., действующие в любом замкнутом контуре, и падения напряжения на сопротивлениях, входящих в данный контур.
Исходя из принципа электрического равновесия, можно сделать логический вывод, что в установившемся режиме, когда токи в контуре не изменяются, все э. д. с. уравновешиваются падениями напряжения.
В самом деле, если предположить, что сумма э. д. с. превышает сумму падений напряжения, то ток в цепи должен возрасти. Наоборот, если сумма падений напряжения превышает сумму э. д. с., то ток должен уменьшиться.
Таким образом, алгебраическая сумма э. д. с., действующих в любом замкнутом контуре, равна алгебраической сумме падений напряжения на всех участках этого контура.
это и есть формулировка второго закона Кирхгофа.
Математически второй закон Кирхгофа выражается формулой:
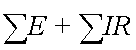
При составлении уравнения второго закона Кирхгофа необходимо учитывать направления токов и э.д.с. для этого выбирают какое либо направление обхода контура (обычно направление движения часовой стрелки) и считают положительными э. д. с, которые создают токи в направлении, совпадающем с направлением обхода и падения напряжения, создаваемые токами, направление которых совпадает с направлением обхода.Так например, на рисунке, обходя контур ABCDA в направлении часовой стрелки, будем считать E1,U1,U3 положительными, а E2 и U2 отрицательными.
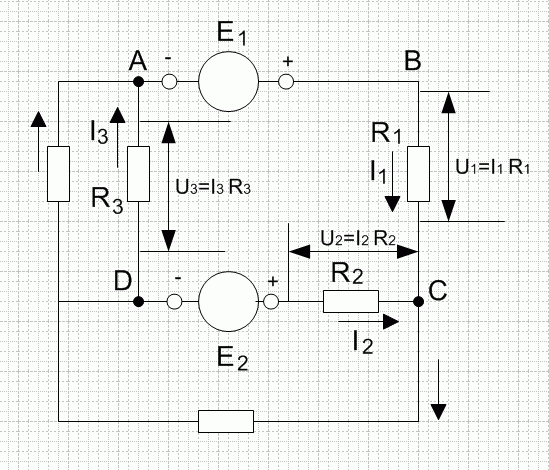
Следовательно, уравнение второго закона Кирхгофа для этого контура запишется так
![]()
К чему применяются????????????
12. МЕТОД УЗЛОВЫХ И КОНТУРНЫХ УРАВНЕНИЙ.
(МЕТОД УРАВНЕНИЙ КИРХГОФА)
Методика решения задачи этим методом.
Направление токов выбирают произвольно. Если в результате решения отдельные токи окажутся отрицательными, то это будет означать, что в действительности они проходят в направлении, противоположном выбранному. Для определения трех неизвестных токов необходимо составить три независимых уравнения, связывающих эти токи. На основании первого закона Кирхгофа для узла «с»:
I1 + I2 — I3 = 0
Уравнение для узла «f» имеет вид:
I3 - I2 - I1 = 0,
то есть совпадает с уравнением для узла «с».
Если сложная цепь имеет n узлов, то число уравнений, которые можно составить на основании первого закона Кирхгофа, на единицу меньше:
n - 1.
Недостающее уравнение можно получить на основании второго закона Кирхгофа. Для контура abcf при обходе по часовой стрелке:
Если направление обхода контура совпадает с направлением ЭДС и токов, то эти ЭДС и соответствующие падания напряжений берутся со знаком «плюс».
При составлении уравнений по второму закону Кирхгофа контуры нужно выбирать так, чтобы каждый из них отличался хотя бы одной ветвью.
Вывод: метод уравнений Кирхгофа сводится к составление системы уравнений в соответствии с первым и вторым законами Кирхгофа и решение этой системы относительно неизвестных токов.
Если электрическая цепь содержит «В» ветвей, то в общем случае необходимо определить «В» токов, т. е. токи в каждой из ветвей. Следовательно общее число уравнений по первому и второму законам Кирхгофа должно быть равно «В».
При числе узлов «У» - число независимых уравнений по первому закону Кирхгофа будет «У — 1», следовательно, остальные «П» уравнений должны быть составлены по второму закону Кирхгофа:
П = В - (У - 1).
Общее число уравнений, составленных по первому и второму законам Кирхгофа, равно числу ветвей, т. е. числу неизвестных токов; это позволяет найти токи во всех ветвях электрической цепи.
13. МЕТОД КОНТУРНЫХ ТОКОВ
Если сложная цепь содержит довольно много узлов и контуров, то ее расчет с помощью первого и второго законов Кирхгофа будет связан с решением большого числа уравнений. Вводя понятие о контурных токах, можно свести уравнения, составленные по законам Кирхгофа, к системе уравнений, составленных только для независимых контуров.
Под контурными токами понимают условные токи, замыкающиеся в соответствующих контурах.
Контурный ток обозначается буквой I с римским индексом, отвечающим номеру независимого контура. Контурный ток равен току в ветви, по которой он протекает индивидуально.
Рассмотрим схему цепи, представленную на рис. 2.14.
Эта схема имеет два независимых контура I и II, в каждом из которых проходят токи I1 и I11. Направления этих токов выбирается произвольными, например по часовой стрелке. Из рассмотрения схемы (рис. 2.14) видно, что реальные токи во внешних ветвях равны контурным: I1 = I1 I3 = I11
Ток во внутренней ветви равен разности контурных токов: I2 = I1 - I11
Для определения контурных токов составим два уравнения:
Собственным сопротивлением контура называется сумма всех сопротивлений в каждом независимом контуре.
Собственное сопротивление обозначается буквой R с двойным индексом соответственно номеру того контура, к которому относится.
Взаимным сопротивлением контуров называется сопротивление, входящее одновременно в каждый из двух смежных контуров.
Взаимное сопротивление обозначается буквой R с двумя индексами соответственно номерам смежных контуров.
Контурной ЭДС называется алгебраическая сумма всех ЭДС в каждом независимом контуре.
Вывод: метод контурных токов сводится к составлению и решению системы уравнений, получаемых только по второму закону Кирхгофа применительно к понятиям контурных токов, сопротивлений и ЭДС.
14. МЕТОД УЗЛОВОГО НАПРЯЖЕНИЯ.
Часто в сложной цепи имеется всего два узла, как, например, в схеме рис. 2.14. В этом случае расчет цепи значительно упрощается, так как достаточно определить так называемое узловое напряжение Uаб.(рис.2.15) После этого токи в ветвях находятся следующим образом:
Все токи в ветвях направляются к узлу, потенциал которого условно принимается за нуль. Узловое напряжение:
где G — проводимость соответствующих ветвей.
Если ЭДС источника направлена к узлу, то произведение ЕG берется со знаком «минус». Токи в ветвях определяются так:
Вывод: метод узлового напряжения сводится к составлению системы уравнений, составленных только по первому закону Кирхгофа; из этих уравнений определяются напряжения в узлах схемы электрической цепи относительно некоторого базисного узла, потенциал которого изначально принимается равным нулю, а токи в ветвях, соединяющих узлы, находят по закону Ома.
15. МЕТОД НАЛОЖЕНИЯ (СУПЕРПОЗИЦИИ)
Этот метод основан на принципе наложения, который утверждает: ток в любой ветви линейной электрической цепи, содержащей несколько источников ЭДС, равен алгебраической сумме токов в этой ветви при действии каждого источника в отдельности. При этом остальные источники заменяются резисторами, имеющими сопротивления, равные внутренним сопротивлениям замененных источников ЭДС.
Справедливость этого принципа следует непосредственно выражения:
Действительно, если в этом выражении положить все ЭДС, кроме Е1, равным нулю, то получим частичный ток I/к в К-й ветви, вызванный действием только ЭДС. E1
Если считать Е2 ≠ 0, а остальные ЭДС равны нулю, то получим частичный ток I//К, вызванный действием только ЭДС Е2и т. д.
Алгебраическая сумма всех частичных токов даст действительный ток, протекающий в к-й ветви.
Принцип наложения применим и к напряжениям, так как они линейно связаны с токами. К расчету же мощности этот принцип применять нельзя, так как мощность является не линейной, а квадратичной формой тока или напряжения: если по участку цепи с сопротивлением R протекает ток I = I1 + I2, то мощность равна:
Р = RI2 = R (I1 + I2)2
а не RI12 + RI22, как формально следовало бы из принципа наложения.
Вывод: метод наложения позволяет найти токи в ветвях без составления и решения системы уравнений, а непосредственно по закону Ома. При этом вначале находят частичные токи от действия каждого источника ЭДС в отдельности, принимая остальные ЭДС равными нулю и оставляя в схеме только их внутренние сопротивления, а затем — действительные токи как алгебраические суммы частичных токов.
16. Нелинейные цепи постоянного тока. Графические методы расчета.
Нелинейные цепи
Нелинейными называются цепи, в состав которых входит хотя бы один нелинейный элемент.
Нелинейными называются элементы, параметры которых зависят от величины и (или) направления связанных с этими элементами переменных (напряжения, тока, магнитного потока, заряда, температуры, светового потока и др.). Нелинейные элементы описываются нелинейными характеристиками, которые не имеют строгого аналитического выражения, определяются экспериментально и задаются таблично или графиками.
Нелинейные элементы можно разделить на двух – и многополюсные. Последние содержат три (различные полупроводниковые и электронные триоды) и более (магнитные усилители, многообмоточные трансформаторы, тетроды, пентоды и др.) полюсов, с помощью которых они подсоединяются к электрической цепи. Характерной особенностью многополюсных элементов является то, что в общем случае их свойства определяются семейством характеристик, представляющих зависимости выходных характеристик от входных переменных и наоборот: входные характеристики строят для ряда фиксированных значений одного из выходных параметров, выходные – для ряда фиксированных значений одного из входных.
По другому признаку классификации нелинейные элементы можно разделить на инерционные и безынерционные. Инерционными называются элементы, характеристики которых зависят от скорости изменения переменных. Для таких элементов статические характеристики, определяющие зависимость между действующими значениями переменных, отличаются от динамических характеристик, устанавливающих взаимосвязь между мгновенными значениями переменных. Безынерционными называются элементы, характеристики которых не зависят от скорости изменения переменных. Для таких элементов статические и динамические характеристики совпадают.
Понятия инерционных и безынерционных элементов относительны: элемент может рассматриваться как безынерционный в допустимом (ограниченном сверху) диапазоне частот, при выходе за пределы которого он переходит в разряд инерционных.
В
зависимости от вида характеристик
различают нелинейные элементы
с симметричными и
несимметричными характеристиками.
Симметричной называется характеристика,
не зависящая от направления определяющих
ее величин, т.е. имеющая симметрию
относительно начала системы координат: ![]() .
Для несимметричной характеристики это
условие не выполняется, т.е.
.
Для несимметричной характеристики это
условие не выполняется, т.е. ![]() .
Наличие у нелинейного элемента
симметричной характеристики позволяет
в целом ряде случаев упростить анализ
схемы, осуществляя его в пределах одного
квадранта.
.
Наличие у нелинейного элемента
симметричной характеристики позволяет
в целом ряде случаев упростить анализ
схемы, осуществляя его в пределах одного
квадранта.
По
типу характеристики можно также разделить
все нелинейные элементы на элементы
с однозначной и неоднозначной
характеристиками.Однозначной
называется характеристика ![]() ,
у которой каждому значению х соответствует
единственное значение y и наоборот. В
случае неоднозначной характеристики
каким-то значениям х может соответствовать
два или более значения y или наоборот.
У нелинейных резисторов неоднозначность
характеристики обычно связана с наличием
падающего участка, для которого
,
у которой каждому значению х соответствует
единственное значение y и наоборот. В
случае неоднозначной характеристики
каким-то значениям х может соответствовать
два или более значения y или наоборот.
У нелинейных резисторов неоднозначность
характеристики обычно связана с наличием
падающего участка, для которого ![]() ,
а у нелинейных индуктивных и емкостных
элементов – с гистерезисом.
,
а у нелинейных индуктивных и емкостных
элементов – с гистерезисом.
Наконец, все нелинейные элементы можно разделить на управляемые и неуправляемые. В отличие от неуправляемых управляемые нелинейные элементы (обычно трех- и многополюсники) содержат управляющие каналы, изменяя напряжение, ток, световой поток и др. в которых, изменяют их основные характеристики: вольт-амперную, вебер-амперную или кулон-вольтную.
Нелинейные электрические цепи постоянного тока
Нелинейные свойства таких цепей определяет наличие в них нелинейных резисторов.
В
связи с отсутствием у нелинейных
резисторов прямой пропорциональности
между напряжением и током их нельзя
охарактеризовать одним параметром
(одним значением ![]() ).
Соотношение между этими величинами в
общем случае зависит не только от их
мгновенных значений, но и от производных
и интегралов по времени.
).
Соотношение между этими величинами в
общем случае зависит не только от их
мгновенных значений, но и от производных
и интегралов по времени.
Параметры нелинейных резисторов
В зависимости от условий работы нелинейного резистора и характера задачи различают статическое, дифференциальное и динамическое сопротивления.
Если нелинейный элемент является безынерционным, то он характеризуется первыми двумя из перечисленных параметров.
С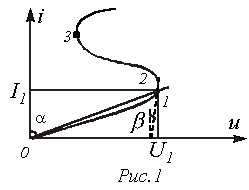 татическое
сопротивление равно отношению
напряжения на резистивном элементе к
протекающему через него току. В частности
для точки 1 ВАХ на рис. 1
татическое
сопротивление равно отношению
напряжения на резистивном элементе к
протекающему через него току. В частности
для точки 1 ВАХ на рис. 1
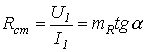 .
.
Под дифференциальным сопротивлением понимается отношение бесконечно малого приращения напряжения к соответствующему приращению тока
![]() .
.
Следует
отметить, что у неуправляемого нелинейного
резистора ![]() всегда,
а
всегда,
а ![]() может
принимать и отрицательные значения
(участок 2-3 ВАХ на рис. 1).
может
принимать и отрицательные значения
(участок 2-3 ВАХ на рис. 1).
В случае инерционного нелинейного резистора вводится понятие динамического сопротивления
![]() ,
,
определяемого
по динамической ВАХ. В зависимости от
скорости изменения переменной, например
тока, может меняться не только величина,
но и знак ![]() .
.
Методы расчета нелинейных электрических цепей постоянного тока
Электрическое состояние нелинейных цепей описывается на основании законов Кирхгофа, которые имеют общий характер. При этом следует помнить, что для нелинейных цепей принцип наложения неприменим. В этой связи методы расчета, разработанные для линейных схем на основе законов Кирхгофа и принципа наложения, в общем случае не распространяются на нелинейные цепи.
Общих методов расчета нелинейных цепей не существует. Известные приемы и способы имеют различные возможности и области применения. В общем случае при анализе нелинейной цепи описывающая ее система нелинейных уравнений может быть решена следующими методами:
графическими;
аналитическими;
графо-аналитическими;
итерационными.
Графические методы расчета
При использовании этих методов задача решается путем графических построений на плоскости. При этом характеристики всех ветвей цепи следует записать в функции одного общего аргумента. Благодаря этому система уравнений сводится к одному нелинейному уравнению с одним неизвестным. Формально при расчете различают цепи с последовательным, параллельным и смешанным соединениями.
а) Цепи с последовательным соединением резистивных элементов.
При
последовательном соединении нелинейных
резисторов в качестве общего аргумента
принимается ток, протекающий через
последовательно соединенные элементы.
Расчет проводится в следующей
последовательности. По заданным
ВАХ ![]() отдельных
резисторов в системе декартовых
координат
отдельных
резисторов в системе декартовых
координат ![]() строится
результирующая зависимость
строится
результирующая зависимость ![]() .
Затем на оси напряжений откладывается
точка, соответствующая в выбранном
масштабе заданной величине напряжения
на входе цепи, из которой восстанавливается
перпендикуляр до пересечения с
зависимостью
.
Затем на оси напряжений откладывается
точка, соответствующая в выбранном
масштабе заданной величине напряжения
на входе цепи, из которой восстанавливается
перпендикуляр до пересечения с
зависимостью ![]() .
Из точки пересечения перпендикуляра с
кривой
опускается
ортогональ на ось токов – полученная
точка соответствует искомому току в
цепи, по найденному значению которого
с использованием зависимостей
определяются
напряжения
.
Из точки пересечения перпендикуляра с
кривой
опускается
ортогональ на ось токов – полученная
точка соответствует искомому току в
цепи, по найденному значению которого
с использованием зависимостей
определяются
напряжения ![]() на
отдельных резистивных элементах.
на
отдельных резистивных элементах.
Применение указанной методики иллюстрируют графические построения на рис. 2,б, соответствующие цепи на рис. 2,а.
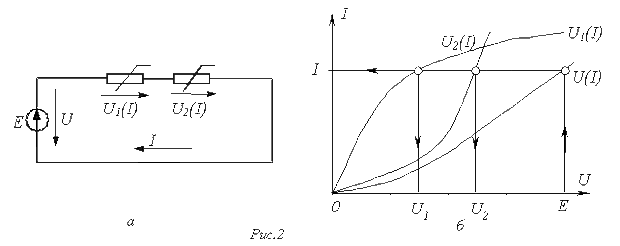
Г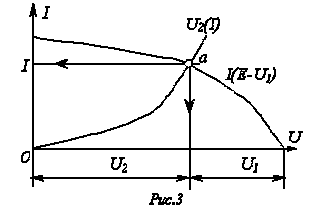 рафическое
решение для последовательной нелинейной
цепи с двумя резистивными элементами
может быть проведено и другим методом
– методом пересечений. В этом
случае один из нелинейных резисторов,
например, с ВАХ
рафическое
решение для последовательной нелинейной
цепи с двумя резистивными элементами
может быть проведено и другим методом
– методом пересечений. В этом
случае один из нелинейных резисторов,
например, с ВАХ ![]() на
рис.2,а, считается внутренним сопротивлением
источника с ЭДС Е, а другой – нагрузкой.
Тогда на основании соотношения
на
рис.2,а, считается внутренним сопротивлением
источника с ЭДС Е, а другой – нагрузкой.
Тогда на основании соотношения ![]() точка
а (см. рис. 3) пересечения кривых
точка
а (см. рис. 3) пересечения кривых ![]() и
и![]() определяет
режим работы цепи. Кривая
строится
путем вычитания абсцисс ВАХ
из
ЭДС Е для различных значений тока.
определяет
режим работы цепи. Кривая
строится
путем вычитания абсцисс ВАХ
из
ЭДС Е для различных значений тока.
Использование данного метода наиболее рационально при последовательном соединении линейного и нелинейного резисторов. В этом случае линейный резистор принимается за внутреннее сопротивление источника, и линейная ВАХ последнего строится по двум точкам.
б) Цепи с параллельным соединением резистивных элементов.
При
параллельном соединении нелинейных
резисторов в качестве общего аргумента
принимается напряжение, приложенное к
параллельно соединенным элементам.
Расчет проводится в следующей
последовательности. По заданным
ВАХ ![]() отдельных
резисторов в системе декартовых
координат
строится
результирующая зависимость
отдельных
резисторов в системе декартовых
координат
строится
результирующая зависимость ![]() .
Затем на оси токов откладывается точка,
соответствующая в выбранном масштабе
заданной величине тока источника на
входе цепи (при наличии на входе цепи
источника напряжения задача решается
сразу путем восстановления перпендикуляра
из точки, соответствующей заданному
напряжению источника, до пересечения
с ВАХ
),
из которой восстанавливается перпендикуляр
до пересечения с зависимостью
.
Затем на оси токов откладывается точка,
соответствующая в выбранном масштабе
заданной величине тока источника на
входе цепи (при наличии на входе цепи
источника напряжения задача решается
сразу путем восстановления перпендикуляра
из точки, соответствующей заданному
напряжению источника, до пересечения
с ВАХ
),
из которой восстанавливается перпендикуляр
до пересечения с зависимостью ![]() .
Из точки пересечения перпендикуляра с
кривой
опускается
ортогональ на ось напряжений – полученная
точка соответствует напряжению на
нелинейных резисторах, по найденному
значению которого с использованием
зависимостей
определяются
токи
.
Из точки пересечения перпендикуляра с
кривой
опускается
ортогональ на ось напряжений – полученная
точка соответствует напряжению на
нелинейных резисторах, по найденному
значению которого с использованием
зависимостей
определяются
токи ![]() в
ветвях с отдельными резистивными
элементами.
в
ветвях с отдельными резистивными
элементами.
Использование данной методики иллюстрируют графические построения на рис. 4,б, соответствующие цепи на рис. 4,а.
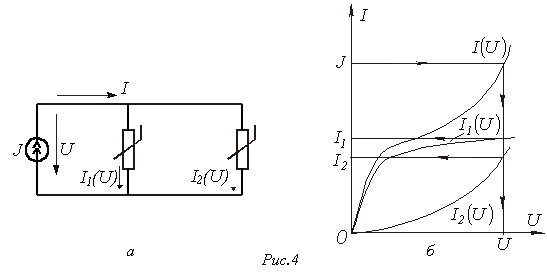
в) Цепи с последовательно-параллельным (смешанным) соединением резистивных элементов.
1. Расчет таких цепей производится в следующей последовательности:
Исходная схема сводится к цепи с последовательным соединением резисторов, для чего строится результирующая ВАХ параллельно соединенных элементов, как это показано в пункте б).
2. Проводится расчет полученной схемы с последовательным соединением резистивных элементов (см. пункт а), на основании которого затем определяются токи в исходных параллельных ветвях.
Метод двух узлов
Для цепей, содержащих два узла или сводящихся к таковым, можно применять метод двух узлов. При полностью графическом способе реализации метода он заключается в следующем:
Строятся
графики зависимостей ![]() токов
во всех i-х ветвях в функции общей величины
– напряжения
токов
во всех i-х ветвях в функции общей величины
– напряжения ![]() между
узлами m и n, для чего каждая из исходных
кривых
между
узлами m и n, для чего каждая из исходных
кривых ![]() смещается
вдоль оси напряжений параллельно самой
себе, чтобы ее начало находилось в точке,
соответствующей ЭДС
смещается
вдоль оси напряжений параллельно самой
себе, чтобы ее начало находилось в точке,
соответствующей ЭДС ![]() в
i-й ветви, а затем зеркально отражается
относительно перпендикуляра,
восстановленного в этой точке.
в
i-й ветви, а затем зеркально отражается
относительно перпендикуляра,
восстановленного в этой точке.
Определяется,
в какой точке графически реализуется
первый закон Кирхгофа ![]() .
Соответствующие данной точке токи
являются решением задачи.
.
Соответствующие данной точке токи
являются решением задачи.
М етод двух узлов может быть реализован и в другом варианте, отличающемся от изложенного выше меньшим числом графических построений.
В качестве примера рассмотрим цепь на рис. 5. Для нее выражаем напряжения на резистивных элементах в функции :
|
(1) |
|
(2) |
|
(3) |
Далее
задаемся током, протекающим через один
из резисторов, например во второй
ветви ![]() ,
и рассчитываем
,
а затем по
с
использованием (1) и (3) находим
,
и рассчитываем
,
а затем по
с
использованием (1) и (3) находим ![]() и
и ![]() и
по зависимостям
и
по зависимостям ![]() и
и ![]() -
соответствующие им токи
-
соответствующие им токи ![]() и
и ![]() и
т.д. Результаты вычислений сводим в
табл. 1, в последней колонке которой
определяем сумму токов
и
т.д. Результаты вычислений сводим в
табл. 1, в последней колонке которой
определяем сумму токов
![]() .
.
Таблица 1. Таблица результатов расчета методом двух узлов
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Алгебраическая
сумма токов в соответствии с первым
законом Кирхгофа должна равнять нулю,
поэтому получающаяся в последней колонке
табл. 1 величина ![]() указывает,
каким значением
следует
задаваться на следующем шаге.
указывает,
каким значением
следует
задаваться на следующем шаге.
В
осях ![]() строим
кривую зависимости
строим
кривую зависимости ![]() и
по точке ее пересечения с осью напряжений
определяем напряжение
между
точками m и n. Для найденного значения
по
(1)…(3) рассчитываем напряжения на
резисторах, после чего по заданным
зависимостям
определяем
токи в ветвях схемы.
и
по точке ее пересечения с осью напряжений
определяем напряжение
между
точками m и n. Для найденного значения
по
(1)…(3) рассчитываем напряжения на
резисторах, после чего по заданным
зависимостям
определяем
токи в ветвях схемы.
17. Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения[1], магнитная составляющая электромагнитного поля[2]
Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты).
Кроме этого, оно появляется при наличии изменяющегося во времени электрического поля.
Основной
силовой характеристикой магнитного
поля является вектор
магнитной индукции ![]() (вектор
индукции магнитного поля)[3][4].
С математической точки зрения
(вектор
индукции магнитного поля)[3][4].
С математической точки зрения ![]() — векторное
поле, определяющее и конкретизирующее
физическое понятие магнитного поля.
Нередко вектор магнитной индукции
называется для краткости просто магнитным
полем (хотя, наверное, это не самое
строгое употребление термина).
— векторное
поле, определяющее и конкретизирующее
физическое понятие магнитного поля.
Нередко вектор магнитной индукции
называется для краткости просто магнитным
полем (хотя, наверное, это не самое
строгое употребление термина).
Ещё одной фундаментальной характеристикой магнитного поля (альтернативной магнитной индукции и тесно с ней взаимосвязанной, практически равной ей по физическому значению) является векторный потенциал.
Нередко в литературе в качестве основной характеристики магнитного поля в вакууме (то есть в отсутствие магнитной среды) выбирают не вектор магнитной индукции
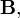 а
вектор напряжённости
магнитного поля
а
вектор напряжённости
магнитного поля  ,
что формально можно сделать, так как в
вакууме эти два вектора совпадают[5];
однако в магнитной среде вектор
не
несет уже того же физического смысла[6],
являясь важной, но всё же вспомогательной
величиной. Поэтому при формальной
эквивалентности обоих подходов для
вакуума, с систематической точки зрения
следует считать основной характеристикой
магнитного поля именно
,
что формально можно сделать, так как в
вакууме эти два вектора совпадают[5];
однако в магнитной среде вектор
не
несет уже того же физического смысла[6],
являясь важной, но всё же вспомогательной
величиной. Поэтому при формальной
эквивалентности обоих подходов для
вакуума, с систематической точки зрения
следует считать основной характеристикой
магнитного поля именно 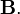
Магнитное поле можно назвать особым видом материи[7], посредством которого осуществляется взаимодействие между движущимися заряженными частицами или телами, обладающими магнитным моментом.
Магнитные поля являются необходимым (в контексте специальной теории относительности) следствием существования электрических полей.
Вместе, магнитное и электрическое поля образуют электромагнитное поле, проявлениями которого являются, в частности, свет и все другие электромагнитные волны.
Напряжённость магнитного поля
[править]
Материал из Википедии — свободной энциклопедии
(перенаправлено с «Напряженность магнитного поля»)
Напряжённость магнитного поля |
|
|
|
Размерность |
L−1I |
Единицы измерения |
|
СИ |
А/м |
СГС |
Э |
Примечания |
|
векторная величина |
|
Напряжённость магни́тного по́ля (стандартное обозначение Н) — векторная физическая величина, равная разности вектора магнитной индукции B ивектора намагниченности M.
В
СИ: ![]() где
где ![]() — магнитная
постоянная.
— магнитная
постоянная.
В
СГС: ![]()
В простейшем случае изотропной (по магнитным свойствам) среды и в приближении достаточно низких частот изменения поля B и H просто пропорциональны друг другу, отличаясь просто числовым множителем (зависящим от среды) B = μ H в системе СГС или B = μ0μ H в системе СИ (см.Магнитная проницаемость, также см. Магнитная восприимчивость).
В системе СГС напряжённость магнитного поля измеряется в эрстедах (Э), в системе СИ — в амперах на метр (А/м). В технике эрстед постепенно вытесняется единицей СИ — ампером на метр.
1 Э = 1000/(4π) А/м ≈ 79,5775 А/м.
1 А/м = 4π/1000 Э ≈ 0,01256637 Э.
[править]Физический смысл
В вакууме (или в отсутствие среды, способной к магнитной поляризации, а также в случаях, когда последняя пренебрежима) напряжённость магнитного поля совпадает с вектором магнитной индукции с точностью до коэффициента, равного 1 в СГС и μ0 в СИ.
В магнетиках (магнитных средах) напряжённость магнитного поля имеет физический смысл «внешнего» поля, то есть совпадает (быть может, в зависимости от принятых единиц измерения, с точностью до постоянного коэффициента, как например в системе СИ, что общего смысла не меняет) с таким вектором магнитной индукции, какой «был бы, если магнетика не было».
Например, если поле создаётся катушкой с током, в которую вставлен железный сердечник, то напряжённость магнитного поля H внутри сердечника совпадает (в СГС точно, а в СИ — с точностью до постоянного размерного коэффициента) с вектором B0, который был бы создан этой катушкой при отсутствии сердечника и который в принципе может быть рассчитан исходя из геометрии катушки и тока в ней, без всякой дополнительной информации о материале сердечника и его магнитных свойствах.
При этом надо иметь в виду, что более фундаментальной характеристикой магнитного поля является вектор магнитной индукции B. Именно он определяет силу действия магнитного поля на движущиеся заряженные частицы и токи, а также может быть непосредственно измерен, в то время как напряжённость магнитного поля H можно рассматривать скорее как вспомогательную величину (хотя рассчитать её, по крайней мере, в статическом случае, проще, в чём и состоит её ценность: ведь H создают так называемые свободные токи, которые сравнительно легко непосредственно измерить, а трудно измеримые связанные токи — то есть токи молекулярные и т. п. — учитывать не надо).
Правда, в обычно используемое выражение для энергии магнитного поля (в среде) B и H входят почти равноправно, но надо иметь в виду, что в эту энергию включена и энергия, затраченная на поляризацию среды, а не только энергия собственно поля[1]. Энергия магнитного поля как такового выражается только через фундаментальное B. Тем не менее видно, что величина H феноменологически и тут весьма удобна.
Закон Био́—Савара—Лапла́са — физический закон для определения вектора индукции магнитного поля, порождаемого постояннымэлектрическим током. Был установлен экспериментально в 1820 году Био и Саваром и сформулирован в общем виде Лапласом. Лаплас показал также, что с помощью этого закона можно вычислить магнитное поле движущегося точечного заряда (считая движение одной заряженной частицы током).
Закон Био—Савара—Лапласа играет в магнитостатике ту же роль, что и закон Кулона в электростатике. Закон Био—Савара—Лапласа можно считать главным законом магнитостатики, получая из него остальные ее результаты.
В современной формулировке закон Био—Савара—Лапласа чаще рассматривают как следствие двух уравнений Максвелла для магнитного поля при условии постоянства электрического поля, т.е. в современной формулировке уравнения Максвелла выступают как более фундаментальные (прежде всего хотя бы потому, что формулу Био—Савара—Лапласа нельзя просто обобщить на общий случай полей, зависящих от времени).
Для тока текущего по контуру (тонкому проводнику)
Пусть
постоянный ток
течёт
по контуру (проводнику) ![]() ,
находящемуся в вакууме,
,
находящемуся в вакууме, ![]() —
точка, в которой ищется (наблюдается)
поле, тогда индукция магнитного
поля в этой точке выражается интегралом
(в Международной
системе единиц (СИ))
—
точка, в которой ищется (наблюдается)
поле, тогда индукция магнитного
поля в этой точке выражается интегралом
(в Международной
системе единиц (СИ))
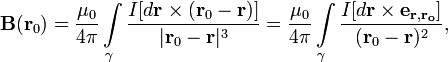
где
квадратными скобками обозначено векторное
произведение, r -
положение точек контура
, dr -
вектор элемента контура, вдоль которого
идет проводник (ток течет вдоль него);
-
константа (магнитная
постоянная); ![]() -
единичный вектор, направленный от
источника к точке наблюдения.
-
единичный вектор, направленный от
источника к точке наблюдения.
В принципе контур может иметь ветвления, представляя собой сколь угодно сложную сеть. В таком случае под выражением, приведенным выше, следует понимать сумму по всем ветвям, слагаемое же для каждой ветви является интегралом приведенного выше вида (контур интегрирования для каждой ветви может быть при этом незамкнутым).
В случае простого (не ветвящегося) контура (и при выполнении условий магнитостатического приближения, подразумевающих отсутствие накопления зарядов), ток I одинаков на всех участках контура и может быть вынесен за знак интеграла. (Это справедливо отдельно и для каждого неразветвленного участка разветвленной цепи).
Если же взять за точку отсчёта точку, в которой нужно найти вектор магнитной индукции, то формула немного упрощается:
![]()
где ![]() -
вектор описывающий кривую проводника
с током
,
-
вектор описывающий кривую проводника
с током
, ![]() -
модуль
,
-
модуль
, ![]() -
вектор магнитной индукции, создаваемый
элементом проводника
-
вектор магнитной индукции, создаваемый
элементом проводника ![]() .
.
Направление ![]() перпендикулярно
плоскости, в которой лежат векторы
перпендикулярно
плоскости, в которой лежат векторы ![]() и
и ![]() .
Направление вектора магнитной индукции
может быть найдено по правилу
правого винта: направление
вращения головки винта дает направление
,
если поступательное движение буравчика
соответствует направлению тока в
элементе. Модуль вектора
определяется
выражением (в системе СИ)
.
Направление вектора магнитной индукции
может быть найдено по правилу
правого винта: направление
вращения головки винта дает направление
,
если поступательное движение буравчика
соответствует направлению тока в
элементе. Модуль вектора
определяется
выражением (в системе СИ)
![]()
Векторный потенциал даётся интегралом (в системе СИ)
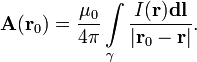
[править]Для распределенных токов
Для случая, когда источником магнитного поля являются распределенные токи, характеризуемые полем вектора плотности тока j, формула закона Био — Савара принимает вид (в системе СИ):
![]()
где j = j(r), dV - элемент объема, а интегрирование производится по всему пространству (или по всем его областям, где j≠0), r - соответствует текущей точке при интегрировании (положению элемента dV).
Векторный потенциал:
![]()
[править]Следствия
Хотя в современном подходе, как правило, сам закон Био-Савара выступает следствием уравнений Максвелла, однако исторически его открытие предшествовало уравнениям Максвелла, поэтому уравнения Максвелла для случая магнитостатики можно рассматривать как следствия закона Био-Савара. С чисто формальной точки зрения в случае магнитостатики оба подхода можно считать равноправными, т.е. в этом смысле то, что из них считать исходными положениями, а что следствиями, зависит от выбора аксиоматизации, который в случае магнитостатики может быть тем или другим с равным формальным правом и практически равным удобством.
Основными следствиями закона Био-Савара являются (в указанном выше смысле) уравнения Максвелла для случая магнитостатики, в интегральной форме имеющие вид
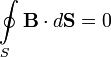
-вариант теоремы Гаусса для магнитного поля (это уравнение остается в электродинамике неизменным и для общего случая)
и
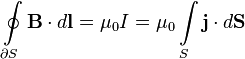
- уравнение для циркуляции магнитного поля в магнитостатике (здесь дано для случая вакуума, в системе СИ). Эта формула (и вывод ее из закона Био-Савара) есть содержаниетеоремы Ампера о циркуляции магнитного поля.
Дифференциальная форма этих уравнений:
![]()
![]()
где j —
плотность тока (запись в системе СИ,
в гауссовой
системе единиц константа
вместо
принимает
вид ![]() ).
).
[править]Вывод из уравнений Максвелла
Закон Био — Савара — Лапласа может быть получен из уравнений Максвелла для стационарного поля. При этом производные по времени равны 0, так что уравнения для поля в вакууме примут вид (в системе СГС)
![]()
![]()
![]()
![]()
где ![]() — плотность
тока в пространстве. При этом
электрическое и магнитное поля оказываются
независимыми. Воспользуемся векторным
потенциалом для магнитного поля (в
системеСГС):
— плотность
тока в пространстве. При этом
электрическое и магнитное поля оказываются
независимыми. Воспользуемся векторным
потенциалом для магнитного поля (в
системеСГС):
![]()
Калибровочная инвариантность уравнений позволяет наложить на векторный потенциал одно дополнительное условие:
![]()
Раскрывая двойной ротор по формуле векторного анализа, получим для векторного потенциала уравнение типа уравнения Пуассона:
![]()
Его частное решение даётся интегралом, аналогичным ньютонову потенциалу:
![]()
Тогда магнитное поле определяется интегралом (в системе СГС)
![]()
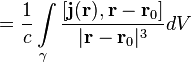
аналогичным по форме закону Био — Савара — Лапласа. Это соответствие можно сделать точным, если воспользоваться обобщёнными функциями и записать пространственную плотность тока, соответствующую витку с током в пустом пространстве. Переходя от интегрирования по всему пространству к повторному интегралу вдоль витка и по ортогональным ему плоскостям и учитывая, что
![]()
получим закон Био — Савара — Лапласа для поля витка с током.
[править]Применение
Допустим
требуется найти модуль магнитной
индукции в центре очень тонкой (все
витки уложены вблизи одной окружности)
катушки с числом витков ![]() ,
по которой течет ток
.
Найдём магнитную индукцию, создаваемую
одним витком катушки. Из формулы
,
по которой течет ток
.
Найдём магнитную индукцию, создаваемую
одним витком катушки. Из формулы
![]()
получим модуль магнитной индукции как
![]()
где
-
как следствие, радиус катушки -
константа, ![]() -
угол между вектором
и
(элемента
витка), ввиду взаимной перпендикулярности,
всегда равен
-
угол между вектором
и
(элемента
витка), ввиду взаимной перпендикулярности,
всегда равен ![]() .
Проинтегрировав обе части получаем
.
Проинтегрировав обе части получаем
![]()
где ![]() -
сумма длин всех элементов проводника
витка или длина окружности, тогда
-
сумма длин всех элементов проводника
витка или длина окружности, тогда
![]()
Так как в катушке содержится витков, то суммарный модуль магнитной индукции равен
![]()
18. Говоря об индукции магнитного поля, прежде всего, стоит разобраться, что собой представляет само магнитное поле, где оно образуется и как определить его наличие.
Итак, магнитное поле представляет собой невидимое для глаза силовое поле, которое может оказывать воздействие на движущиеся электрические заряды, а также тела, которые обладают магнитным моментом. Само магнитное поле появляется в результате движения заряженных частиц, таким образом, мы можем его наблюдать вокруг абсолютно любых проводников, по которым движется ток. Но существуют и постоянные магниты, вокруг которых мы так же можем наблюдать магнитное поле, хотя и в меньшей степени.
Ниже на иллюстрации, наглядно показано с помощью железной стружки, как на самом деле выглядит магнитное поле (Рис. 1). Итак, мы разобрались, что собой представляет магнитное поле, теперь подробнее обратим внимание на одну из основных его характеристик, а именно магнитную индукцию.
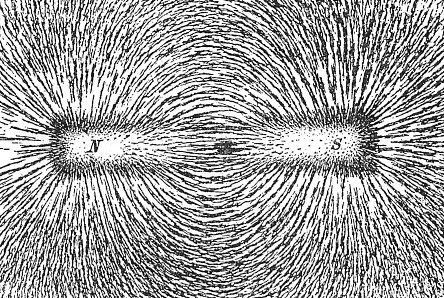
Рисунок 1
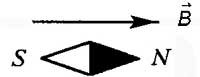
Рисунок 2
Индукция магнитного поля – это векторная физическая величина, которая является силовой характеристикой магнитного поля. Направление магнитной индукции совпадает с направлением, который указывает магнитная стрелка в магнитном поле (Рис. 2), а модуль данной величины равен отношению модуля магнитной силы, которая действует на движущуюся перпендикулярно заряженную частицу, к модулю скорости и заряда этой частицы. Магнитная индукция согласно СИ измеряется в теслах (Тл).
Таким образом, можем записать формулу, которая показывает числовое значение магнитной индукции, хотя магнитная индукция это векторная величина мы обратим внимание на ее модуль.
Индукция магнитного поля, формула
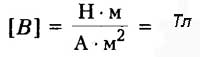 Исходя
из того, что вектор магнитной индукции
считается одной из физических величин,
которая является фундаментальной
в теории электромагнетизма, его можно
встретить в огромном множестве уравнений,
в каких-то случаях непосредственно, а
иногда через напряженность магнитного
поля, связанную с ним. Так что, по сути,
единственной областью в классической
теории электромагнетизма, в которой
отсутствует вектор магнитной индукции,
является, пожалуй, только чистая
электростатика.
Исходя
из того, что вектор магнитной индукции
считается одной из физических величин,
которая является фундаментальной
в теории электромагнетизма, его можно
встретить в огромном множестве уравнений,
в каких-то случаях непосредственно, а
иногда через напряженность магнитного
поля, связанную с ним. Так что, по сути,
единственной областью в классической
теории электромагнетизма, в которой
отсутствует вектор магнитной индукции,
является, пожалуй, только чистая
электростатика.
Индукция магнитного поля бесконечного соленоида
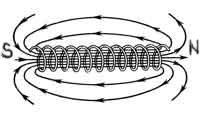
Рисунок 3
Особый интерес представляет индукция магнитного поля внутри соленоида, длина которого в значительной степени превосходит его диаметр. Любой соленоид представляет собой катушку с одинаковыми витками проволоки, наглядно он показан на рис.3. Магнитная индукция внутри такого соленоида повсюду имеет одинаковое направление, которое параллельно оси соленоида, а это значит, что линии поля между собой параллельны.
Индукция магнитного поля бесконечного соленоида, измеряемая внутри него различными способами в разных точках соленоида, показывает, что если витки соленоида располагаются равномерно, то магнитная индукция внутри соленоида во всех точках имеет, как одинаковое направление, так и одинаковое числовое значение. Отсюда вывод, что магнитное поле внутри бесконечного равномерно навитого соленоида является однородным.
Индукция магнитного поля в центре кругового тока
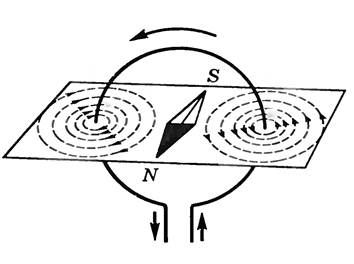
Рисунок 4
Напоследок приведем еще один интересный факт, который уже касается кругового тока. Исследования доказали, что индукция магнитного поля в центре кругового тока, а точнее ее линии не составляют правильные окружности (рис. 4), однако они замыкаются, обходя при этом проводник с током. Здесь направление линий индукции магнитного поля определяется при помощи правила буравчика (правого винта): если буравчик вращать в направлении течения тока в проводнике, то движение острия винта укажет направление индукции магнитного поля в центре кругового тока.
19. Кривая намагничивания и петля гистерезиса
Ферромагнитные материалы благодаря их способности намагничиваться широко применяют при изготовлении электрических машин, аппаратов в других электротехнических установок. Основными характеристиками их являются: кривая намагничивания, ширина петли гистерезиса и потери мощности при перемагничивании.
Процесс намагничивания ферромагнитного материала можно изобразить в виде кривой намагничивания в соответствии с рисунком 9, которая представляет собой зависимость индукции В от напряженности Н магнитного поля. Так как напряженность магнитного поля определяется силой тока, посредством которого намагничивается ферромагнитный материал, эту кривую можно рассматривать как зависимость индукции от намагничивающего тока I.
Кривую намагничивания можно разбить на три участка: Оа, на котором магнитная индукция возрастает почти пропорционально намагничивающему току (напряженности поля); а-б, на котором рост магнитной индукции замедляется («колено» кривой намагничивания), и участок магнитного насыщения за точкой б, где зависимость В от H становится опять прямолинейной, но характеризуется медленным нарастанием магнитной индукции при увеличении напряженности поля по сравнению с первым и вторым участками кривой.
Следовательно, при большом насыщении ферромагнитные вещества по способности пропускать магнитный поток приближаются к неферромагнитным материалам (магнитная проницаемость их резко уменьшается). Магнитная индукция, при которой происходит насыщение, зависит от рода ферромагнитного материала.
Рисунок 9
Чем больше индукция насыщения ферромагнитного материала, тем меньший намагничивающий ток требуется для создания в нем заданной индукции и, следовательно, тем лучше он пропускает магнитный поток.
Магнитную индукцию в электрических машинах, аппаратах и приборах выбирают в зависимости от предъявляемых к ним требований. Если необходимо, чтобы случайные колебания намагничивающего тока мало влияли на магнитный поток данной машины или аппарата, то выбирают индукцию, соответствующую условиям насыщения (например, в генераторах постоянного тока с параллельным возбуждением). Если желательно, чтобы индукция и магнитный поток изменялись пропорционально намагничивающему току (например, в электроизмерительных приборах), то выбирают индукцию, соответствующую прямолинейному участку кривой намагничивания.
Большое практическое значение, особенно в электрических машинах и установках переменного тока, имеет процесс перемагничивания ферромагнитных материалов. На рисунке 10 показан график изменения индукции при намагничивании и размагничивании ферромагнитного материала (при изменении намагничивающего тока I или напряженности магнитного поля Н).
Рисунок 10
Как видно из этого графика, при одних и тех же значениях напряженности магнитного поля магнитная индукция, полученная при размагничивании ферромагнитного тела (участок а-б-в), будет больше индукции, полученной при намагничивании (участки О-а и д-а). Когда напряженность поля (намагничивающий ток) будет доведена до нуля, индукция в ферромагнитном материале не уменьшится до нуля, а сохранит некоторое значение Вr соответствующее отрезку Об. Это значение называется остаточной индукцией.
Явление отставания, или запаздывания, изменений магнитной индукции от соответствующих изменений напряженности магнитного поля называется магнитным гистерезисом, а сохранение в ферромагнитном материале магнитного поля после прекращения протекания намагничивающего тока - остаточным магнетизмом.
При изменении направления намагничивающего тока можно полностью размагнитить ферромагнитное тело и довести магнитную индукцию в нем до нуля. Обратная напряженность Нс, при которой индукция в ферромагнитном материале уменьшается до нуля, называется коэрцитивной силой. Кривую О-а, получающуюся при условии, что ферромагнитное вещество было предварительно размагничено, называют первоначальной кривой намагничивания.
Следовательно, при перемагничивании ферромагнитного вещества, например при постепенном намагничивании и размагничивании стального сердечника электромагнита, кривая изменения индукции будет иметь вид петли; ее называют петлей гистерезиса.
ферромагнетик парамагнетик петля гистерезиса
20.
Зако́н Ампе́ра —
закон взаимодействия электрических
токов. Впервые был установлен Андре
Мари Ампером в 1820 для
постоянного тока. Из закона Ампера
следует, что параллельные проводники с
электрическими токами, текущими в одном
направлении, притягиваются, а в
противоположных — отталкиваются.
Законом Ампера называется также закон,
определяющий силу, с которой магнитное
поле действует на малый
отрезок проводника с током. Выражение
для силы ![]() ,
с которой магнитное поле действует на
элемент объёма
,
с которой магнитное поле действует на
элемент объёма ![]() проводника
с током плотности
проводника
с током плотности ![]() ,
находящегося в магнитном поле с
индукцией
,
находящегося в магнитном поле с
индукцией ![]() ,
в Международной
системе единиц (СИ) имеет
вид:
,
в Международной
системе единиц (СИ) имеет
вид:
![]() .
.
Если
ток течёт по тонкому проводнику, то ![]() ,
где
,
где ![]() —
«элемент длины» проводника — вектор,
по модулю равный
—
«элемент длины» проводника — вектор,
по модулю равный ![]() и
совпадающий по направлению с током.
Тогда предыдущее равенство можно
переписать следующим образом:
и
совпадающий по направлению с током.
Тогда предыдущее равенство можно
переписать следующим образом:
-
Сила , с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока в проводнике и векторному произведению элемента длины проводника на магнитную индукцию :
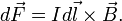
Направление силы определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила левой руки.
Модуль силы Ампера можно найти по формуле:
![]()
где — угол между векторами магнитной индукции и тока.
Сила ![]() максимальна
когда элемент проводника с током
расположен перпендикулярно линиям
магнитной индукции (
максимальна
когда элемент проводника с током
расположен перпендикулярно линиям
магнитной индукции (![]() ):
):
![]()
Проводник с током в магнитном поле. Энергия, заключенная в магнитном поле, может проявлять себя в виде электромагнитных сил, которые возникают при взаимодействии магнитного поля с движущимися электрическими зарядами. Электромагнитная сила, возникающая при движении электрического заряда в магнитном поле, действует на него в направлении, перпендикулярном движению и направлению силовых линий, и стремится вытолкнуть заряд за пределы поля (см. рис. 34).
Если поместить в магнитное поле проводник с током I, то между электронами, проходящими по проводнику, и магнитным полем возникнут электромагнитные силы, которые, складываясь, образуют результирующую силу F, стремящуюся вытолкнуть проводник из магнитного поля (рис. 48). Электромагнитная сила определяется законом Ампера. Он формулируется следующим образом.Электромагнитная сила, действующая на проводник с током, находящийся в магнитном поле и расположенный перпендикулярно направлению поля, равна произведению силы тока I, индукции магнитного поля В и длины проводника l:
F = IBl (48)
Если проводник расположен под углом ? к силовым магнитным
F = BIlsin? (48′)
Чтобы получить F в ньютонах, надо В брать в теслах, I — в амперax и l — в метрах.
Направление действия силы F обычно определяют по правилу левой руки: ладонь левой руки нужно расположить так, чтобы магнитные линии входили в нее и четыре вытянутых пальца совместить с направлением тока, тогда расположенный под прямым углом большой палец укажет направление действия электромагнитной силы. Сила F возникает только в том случае, если проводник расположен перпендикулярно или под некоторым углом к магнитным силовым линиям поля. Если же проводник расположен вдоль силовых линий поля, то электромагнитная сила будет равна нулю.
Для того чтобы изменить направление электромагнитной силы, как следует из правила левой руки, необходимо изменить направление тока в проводнике или же направление магнитного поля.
Возникновение электромагнитной силы F при взаимодействии проводника с током и магнитного поля можно наглядно представить как результат взаимодействия двух магнитных полей. Как известно, вокруг проводника с током возникает свое собственное круговое магнитное поле (рис. 49), которое будет складываться с внешним магнитным полем (например, постоянного магнита), в которое помещен проводник с током. При этом справа от проводника, где силовые линии поля проводника совпадают с линиями внешнего поля, происходит сгущение силовых линий; слева от проводника, где силовые линии поля проводника направлены навстречу линиям внешнего поля, происходит разрежение силовых линий. Магнитные силовые линии обладают свойством упругости, напоминающим свойство резиновых нитей. Стремясь сократиться по длине, они будут выталкивать проводник из области сгущения силовых линий в сторону их разрежения, т. е. справа налево. В результате возникает электромагнитная сила F.
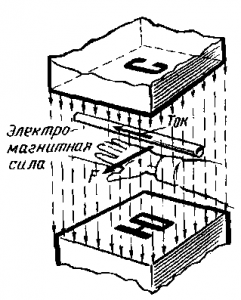 Рис.
48. Электромагнитная сила, действующая
в магнитном поле на проводник с током
Рис.
48. Электромагнитная сила, действующая
в магнитном поле на проводник с током
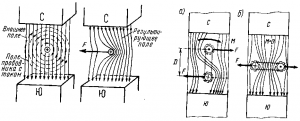 Рис.
49. Сгущение и разрежение магнитных
силовых линий при наличии в магнитном
поле проводника с током.
Рис.
49. Сгущение и разрежение магнитных
силовых линий при наличии в магнитном
поле проводника с током.
Рис. 50.Электромагнитные силы,действующие в магнитном поле на виток или катушку с током.
21. МАГНИТНЫЙ ПОТОК - поток Ф вектора магнитной индукции В через к--л. поверхность S:

Здесь dS -
элемент площади, п - единичный
вектор нормали к S. В СИ М. п.
измеряется в веберах (Во), в гауссовой
системе единиц (к-рая применяется ниже)
- в максвеллах (Мкс); 1 Вб=108 Мкс.
Поскольку вектор В является
чисто вихревым ![]() ,
М. п. через произвольную замкнутую
поверхность S равен нулю. Это
свойство, установленное Гауссом, может
нарушаться только при наличии внутриS
магнитных монополей, пока ещё
гипотетических.
,
М. п. через произвольную замкнутую
поверхность S равен нулю. Это
свойство, установленное Гауссом, может
нарушаться только при наличии внутриS
магнитных монополей, пока ещё
гипотетических.
Изменение во времени М. п. ведёт, согласно Максвелла уравнениям (в интегральной форме), к возникновению вихревого электрич. поля Е, циркуляция к-рого по замкнутому контуру l, ограничивающему поверхность S, равна
![]()
Здесь направление обхода по l связано с направлением нормали п к S правилом правого винта.
Для проводящих контуров, изготовленных из материалов с достаточно высокой проводимостью (напр., из металлич. провода), соотношение (2) в квазистатич. приближении соответствует закону электромагнитной индукции Фарадея:
![]()
где
-эдс эл--магн. индукции, ![]() -
М. п., "сцепленный"
-
М. п., "сцепленный" ![]() с
проводящим контуром, т. е. М. п., усреднённый
по всем поверхностям Si,
опирающимся на линии тока в контуре. В
отличие от (2), в (3) берётся полная
производная от М. п. по времени в
соответствии с тем, что эдс индукции
возникает не только при изменении магн.
поля во времени, но и при движении
проводящего контура поперёк магн. поля,
при вращениях и деформациях контура.
с
проводящим контуром, т. е. М. п., усреднённый
по всем поверхностям Si,
опирающимся на линии тока в контуре. В
отличие от (2), в (3) берётся полная
производная от М. п. по времени в
соответствии с тем, что эдс индукции
возникает не только при изменении магн.
поля во времени, но и при движении
проводящего контура поперёк магн. поля,
при вращениях и деформациях контура.
М. п.,
сцепленный со свсрхпроводящим контуром,
постоянен во времени и может принимать
лишь дискретные (квантованные)
значения: ![]() ,
где h - постоянная
Планка, е - заряд электрона,
и - целое число (см. Квантование
магнитного потока).Величина
кванта М. п. указывает на то, что носители
электрич. тока в сверхпроводнике
(куперовские пары) имеют заряд 2е.
,
где h - постоянная
Планка, е - заряд электрона,
и - целое число (см. Квантование
магнитного потока).Величина
кванта М. п. указывает на то, что носители
электрич. тока в сверхпроводнике
(куперовские пары) имеют заряд 2е.
М. п.
может направляться стержнями (обычно
ферромагнитными) с магнитной
проницаемостью![]() (см. Магнитная
цепь ),подобно тому как
электрич. ток направляется проводами
с большой электропроводностью. На
границе магнитопровода с окружающим
пространством (вакуумом)
непрерывна нормальная компонента
вектора магн. индукции:
(см. Магнитная
цепь ),подобно тому как
электрич. ток направляется проводами
с большой электропроводностью. На
границе магнитопровода с окружающим
пространством (вакуумом)
непрерывна нормальная компонента
вектора магн. индукции:![]() -
внутр. и внеш. поле магн. индукции), а
тангенциальная составляющая терпит
скачок:
-
внутр. и внеш. поле магн. индукции), а
тангенциальная составляющая терпит
скачок: ![]() .
Поэтому при
.
Поэтому при ![]() и
при почти произвольной ориентации внеш.
магн. поля (исключение составляет случай,
когда поле нормально к границе) вектор
магн. индукции
и
при почти произвольной ориентации внеш.
магн. поля (исключение составляет случай,
когда поле нормально к границе) вектор
магн. индукции![]() почти
параллелен границе и его величина много
больше
почти
параллелен границе и его величина много
больше ![]() ,
а М. п. слабо меняется вдоль магнитопровода.
Это свойство ферромагн. материалов
широко используется в электротехнике
для сосредоточения и переноса М. и.
(напр., в трансформаторах, пост. магнитах,
якорях электродвигателей).
,
а М. п. слабо меняется вдоль магнитопровода.
Это свойство ферромагн. материалов
широко используется в электротехнике
для сосредоточения и переноса М. и.
(напр., в трансформаторах, пост. магнитах,
якорях электродвигателей).
22.
Индуктивное влияние. Магнитный поток, потокосцепление, индуктивность |
Если электрические заряды равномерно движутся, то они создают магнитное поле. Основным свойством поля является его силовое взаимодействие с проводниками, с током. Для характеристики поля вводится векторная величина – магнитная индукция В. Измеряется магнитная индукция в теслах (Тл). Опытным путем установлено, что магнитная индукция вокруг линейного элемента dl с током I определяется выражением
где μ0 – магнитная постоянная, равная 4π∙10-7гн/м; 1R – единичный вектор, направленный по кратчайшему расстоянию от оси провода до точки наблюдения; R – расстояние от оси провода до точки наблюдения. Если контур с током находится в каком-либо веществе, то величина магнитной индукции будет в μ раз больше
Безразмерная величина μ называется магнитной проницаемостью. Произведение μ∙μ0 = μа называется абсолютной магнитной проницаемостью. Другим основным вектором магнитного поля является вектор напряженности Н, равный магнитной индукции В, деленной на абсолютную магнитную проницаемость.
Для линейного проводника с током
Поток вектора магнитной индукции
Опытом установлено, что магнитный поток сквозь замкнутую поверхность равен нулю
Это равенство справедливо для любого объема. Следовательно, divB = 0. (4.61) Формула (4.61) выражает принцип направленности магнитного потока. Магнитное поле не имеет истоков. Основным законом, характеризующим свойство магнитного поля, является закон полного тока
Так как
то получаем
где δ – плотность тока. Уравнения (4.62), (4.63) являются основными для расчета магнитных полей. Потокосцепление – более сложное понятие, чем магнитный поток. Магнитный поток по определению связан с поверхностью (выражение (4.60). Потокосцепление связано с таким понятием, как контур. Пусть имеется одновитковый контур. Поток Φ пронизывает поверхность, ограниченную этим контуром. Если контур сделать многовитковым (w витков), то магнитный поток, сцепленный с w витков будет в w раз больше и его принято называть потокосцеплением Ψ.
С другой стороны, потокосцепление с током связано соотношением
где L – коэффициент пропорциональности, называемый собственной индуктивностью. Магнитная энергия, накопленная контуром, равна
Индуктивность L – это свойство, зависящее от параметров объекта, магнитной проницаемости среды, окружающей объект и от магнитной проницаемости материала самого объекта. Индуктивность проявляется, когда протекает ток, и характеризует способность тела создавать потокосцепление, т.е. способность накапливать магнитную энергию. При наличии двух контуров существует явление, когда протекает ток в первом контуре и создает потокосцепление Ψ1. Часть созданного магнитного потока Ψ21 сцепляется с контуром два. Величина потокосцепления Ψ21 определяется током I1 в контуре 1 выражением Ψ21= М ∙I1, (4.68) М – взаимная индуктивность, коэффициент пропорциональности в выражении (4.68). М зависит от геометрических размеров обоих контуров, магнитной проницаемости обоих объектов и характеризует способность контура II накапливать магнитную энергию при протекании тока в контуре I. |
23. Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.
Электромагнитная индукция была открыта Майклом Фарадеем 29 августа[источник не указан 93 дня] 1831 года. Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы (ЭДС) не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.
Закон электромагнитной индукции (закон Фарадея):
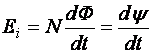 ,
(39)
,
(39)
где ![]() – эдс индукции;
– эдс индукции; ![]() –
полный магнитный поток (потокосцепление).
–
полный магнитный поток (потокосцепление).
24. джоуля - ленца закон
ДЖОУЛЯ
- ЛЕНЦА ЗАКОН - количество теплоты Q,
выделяющейся в единицу времени на
участке электрич. цепи с сопротивлениемR при
протекании по нему пост. тока I,
равно Q=RI2. При дифференц.
описании Д. -Л. з. имеет вид локального
соотношения ![]()
![]() ,
где q - объёмная плотность выделяемой
теплоты, j- плотность тока,
,
где q - объёмная плотность выделяемой
теплоты, j- плотность тока, ![]() -
уд. сопротивление,
-
уд. сопротивление, ![]() -
электропроводность среды.
-
электропроводность среды.
Закон установлен в 1841 Дж. П. Джоулем и подтверждён в 1842 точными опытами Э. X. Ленца. Ленцу принадлежит также экспери м. определение условий оптим. отдачи энергии источника в нагрузку: количество теплоты, выделяемой на сопротивлении нагрузки и на внутр. сопротивлении источника, должно быть одинаково (см. также Джоулевы потери).
Д. -Л.
з. в его первонач. формулировке справедлив
для линейных изотропных сред без
дисперсии, когда соблюдается закон
Ома: ![]() (
(![]() -
напряжённость электрич. поля). Однако
Д--Л. з. допускает разл. обобщения и может
быть распространён на перем. токи
(см. Пойнтинга
вектор). А А. Жаров.
-
напряжённость электрич. поля). Однако
Д--Л. з. допускает разл. обобщения и может
быть распространён на перем. токи
(см. Пойнтинга
вектор). А А. Жаров.
Русский ученый Ленц и английский физик Джоуль одновременно и независимо один от другого установили, чтопри прохождении электрического тока по проводнику количество теплоты, выделяемое проводником, прямо пропорционально квадрату тока, сопротивлению проводника и времени, в течение которого электрический ток протекал по проводнику. Это положение называется законом Ленца — Джоуля.
25.
Явление
самоиндукции заключается в появлении
ЭДС индукции в самом проводнике при
изменении тока в нем. Примером явления
самоиндукции является опыт с двумя
лампочками, подключенными параллельно
через ключ к источнику тока, одна из
которых подключается через катушку
(рис. 39). При замыкании ключа лампочка
2, включенная через катушку, загорается
позже лампочки 1. Это происходит потому,
что после замыкания ключа ток достигает
максимального значения не сразу,
магнитное поле нарастающего тока породит
в катушке индукционную ЭДС, которая в
соответствии с правилом Ленца будет
мешать нарастанию тока.
Для самоиндукции выполняется установленный
опытным путем закон: ЭДС самоиндукции
прямо пропорциональна скорости изменения
тока в проводнике.![]() .
.
Проявление явления самоиндукции:
При выключении тока между подвижными контактами проскакивает искра
Применение явления самоиндукции:
Работа ламп дневного света
Электрические колебания в колебательном контуре
26. Взаимоиндукция
Е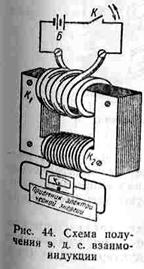 сли
две катушки находятся на некотором
расстоянии друг от друга и по одной из
них К1 проходит
изменяющийся ток, то часть магнитного
потока, возбуждаемого этим током,
пронизывает (пересекает) витки второй
катушки К2 и в ней
возникает э. д. с, называемая э. д.
с. взаимоиндукции (рис.
44).
сли
две катушки находятся на некотором
расстоянии друг от друга и по одной из
них К1 проходит
изменяющийся ток, то часть магнитного
потока, возбуждаемого этим током,
пронизывает (пересекает) витки второй
катушки К2 и в ней
возникает э. д. с, называемая э. д.
с. взаимоиндукции (рис.
44).
Под действием э. д. с. взаимоиндукции в замкнутой цепи второй катушки возникает электрический ток взаимоиндукции. Он вызывает появление магнитного поля, которое пронизывает витки первой катушки, в результате чего в ней также возникает э. д. с. взаимоиндукции. Такое явление называется взаимоиндукцией.
Величина
э. д. с. взаимоиндукции, возникающей
во второй катушке, зависит от размеров,
расположения катушек, магнитной
проницаемости их сердечника, а также
от скорости изменения силы тока ![]() в
первой катушке. Эту зависимость можно
выразить формулой.
в
первой катушке. Эту зависимость можно
выразить формулой.
![]()
где ∆I — изменение силы тока (а) за время ∆t, сек;
М — величина, зависящая от размеров катушек, их расположения и магнитной проницаемости среды между катушками. Она, называется взаимной индуктивностью и измеряется в генри (гн).
Знак минус в этой формуле показывает, что э. д. с. взаимоиндукции противодействует причине, вызывающей ее.
Взаимной индуктивностью в 1 гн обладают две цепи в том случае, если в одной из них возникает э. д. с. взаимоиндукции в 1 в при равномерном изменении тока в другой цепи со скоростью 1 а в 1 сек.
На использовании явления взаимоиндукции основано действий трансформаторов.
Явление взаимоиндукции широко используются в трансформаторах, радиотехнических устройствах и устройствах автоматики.
27. Электрическая емкость. Конденсаторы
Устройство, состоящее из двух или более проводников (пластин), разделенных диэлектриком, называется конденсатором, а проводники — обкладками конденсатора. Важнейшее свойство конденсатора заключается в том, что он может накапливать определенное количество электричества. Если присоединить пластины к источнику тока, то в конденсатор потечет зарядный ток. При отключении источника заряд останется на конденсаторе. Разноименные заряды будут удерживаться на обеих пластинах определенное время. Если конденсатор замкнуть на сопротивление, то под действием напряжения в цепи будет протекать ток разряда конденсатора. Напряженность электрического поля конденсатора представляет собой отношение напряжения на обкладках к расстоянию между ними: Е = U/I. Свойство конденсатора накапливать электрические заряды характеризует его емкость. Емкость конденсатора — это величина, численно равная заряду, накопленному конденсатором при напряжении между обкладками в 1 В: C=q/U, где С — емкость конденсатора, Ф; q — величина заряда, Кл; U —напряжение, В. Фарада — очень крупная единица, и поэтому для измерения емкости пользуются микрофарадами и пикофара-дами: ! микрофарада (мкФ) = 0,000001 Ф = 10-12Ф, 1 пикофарада (пФ) =10-12 Ф. Емкость плоского конденсатора зависит от площади его обкладок, расстояния между ними и диэлектрической проницаемости изолирующего материала (диэлектрика), разделяющего обкладки: C=eaS/d, где S — площадь каждой пластины, м2; d — расстояние между пластинами, м. Емкость цилиндрического конденсатора ^ С = = 2п/еа/1п -А где l — длина цилиндра, м; d\ и di — дна- d метр внутреннего и внешнего цилиндра, мм; In — — а\ натуральный логарифм числа d3/d\. Энергия, запасенная в электрическом поле конденсатора, W=CU*/2. Если напряженность электрического поля в диэлектрике между обкладками конденсатора превысит предельную величину, то электрический заряд будет переходить с одной обкладки на другую через массу диэлектрика, что вызовет повреждение (пробой) изолирующего слоя конденсатора. Это явление происходит, когда электрическое напряжение между проводниками (электродами), разделенными диэлектриком, достигает некоторого предельного (пробивного) значения. Чем толще слой данного электроизоляционного материала, тем выше его пробивное напряжение. Пробивное напряжение слоя электроизоляционного материала, деленное на толщину слоя, численно представляет собой электрическую прочность данного электроизоляционного материала (табл. 1). Электрическая прочность измеряется в В/см, В/м, кВ/см, кВ/мм. Когда диэлектрик применяется как электроизолирующий материал, прикладываемое к нему напряжение выбирают значительно ниже пробивного для того, чтобы обеспечить надежную и длительную работу установок. Отношение пробивного напряжения к рабочему напряжению изоляции называется коэффициентом запаса электрической прочности изоляции. Пробой диэлектриков в конденсаторах, электрических машинах, трансформаторах, кабелях часто является причиной аварии. В некоторых случаях, наоборот, пробой диэлектриков находит практическое применение для технических целей. Так, например, электрический разряд в газах (пробой газа) используют в газосветных лампах для освещения, пробой в специальных разрядниках — для защиты от перенапряжений. В зависимости от типа диэлектрика, разделяющего обкладки, конденсаторы бывают бумажные, слюдяные, керамические, электролитические и воздушные. Промышленность выпускает конденсаторы постоянной, переменной и полупеременной емкости. ^ Применяются конденсаторы в промышленности для компенсации реактивной мощности, в колебательных контурах в радио и телевизионной технике, в электрических фильтрах.
Расчет?????????????????????????????????????????????????????????

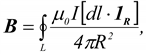 (4.57)
(4.57)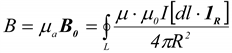 (4.58)
(4.58) .
.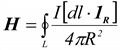 .
(4.59)
.
(4.59)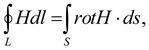 (4.63)
(4.63)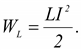 (4.67)
(4.67)