29Linear mapping. Injective and surjective linear mappings. Matrix of a linear mapping.
In
those cases when the image of an operator doesn’t belong to the
domain we say on a mapping. A mapping A
of a set
to a set
is called injective
(or an injection)
if
implies
for all
.A
mapping A
of a set
to a set
is called surjective
(or a surjection)
if every element of
has a pre-image in
.
Theorem.
The matrix
of
a linear mapping A
in bases
and
is connected with the matrix
of this mapping in bases
and
by the following:
where
is the transition matrix from the basis
to the basis
,
and
is the transition matrix from the basis
to the basis
.
30Linear functionals. The components of a linear functional. Dual space of linear functional
Consider
a special case of a linear operator when its imageis contained in a
one-dimensional linear space that is isomorphic to the set of real
numbers. Let every element of a linear space
is assigned a uniquely definable number denoted by
In this case we say a functional
is given in
.
Lemma. The sum of two linear functionals is a linear functional.
Zero
functional is the functional
assigning to every element of a linear space
the number 0. A functional that is opposite
to a linear functional
is the functional assigning to every element of a linear space
the number
.
Obviously, zero and opposite functionals are linear and for every
the following equalities are true:
The
product
of
a linear functional f(x)
on number
is the functional assigning to every element of a linear space
the number
.
Lemma. The product of a linear functional on number is linear and the following equalities hold:
Theorem.
The set of all linear functionals given in a linear space
is a linear space denoted by
.
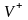A linear space of linear functionals given in is called dual (or conjugate) to the space .
28.The image and kernel of a linear operator.
The image (or range) of a linear operator A is the set of images of all elements , i.e. elements Ax. It is denoted by . Thus, .
Obviously, for every linear operator its domain coincides with V. The answer on the question “What is the image of a linear operator?” gives the following:
Theorem 1. Let A be a linear operator acting in a linear space V. Then
1. The set of elements is a subspace of V.
2. If V is an n-dimensional space with a basis , then the dimension of is equal to the rank of the matrix .
The rank of a linear operator A is called the dimension of its image.
Corollary 1. The rank of a linear operator A is equal to and doesn’t depend on choice of a basis .
Corollary 2. The dimension of the image of a linear operator A acting on some subspace of a linear space V doesn’t exceed . Other important characteristic of a linear operator is the collection of elements of a linear space V called the kernel of the linear operator and denoted by ker A. The kernel of a linear operator A consists of elements such that . Thus, ker . Theorem 4. If V is an n-dimensional linear space and , then ker A is a subspace of V and .