Лекция 05

2. Частотные критерии устойчивости. Вспомним, что уравнение первого приближения выглядит так: .

, где s_n – корни характеристического уравнения первого приближения. Заменим s на jω, получим:

Критерий устойчивости Михайлова. Пусть есть m правых корней и (n-m) левых, тогда приращение аргумента характеристического уравнения первого приближения при изменении ω от -∞ до ∞ будет равняться (∆ - приращение):

Если , то это чётная функция. Если – нечётная.

Кривая, которую описывает своим концом вектор характеристического уравнения первого приближения при изменении ω от 0 до ∞ называется годографом системы.

Для того, чтобы система была устойчивой, необходимо и достаточно, чтобы годограф системы последовательно обходил n квадрантов в положительном направлении.

Критерий устойчивости Найквист-Михайлова.

В числителе только полюса и нули. В знаменателе – полюса.

φ не должен охватывать точку (0;0).

В том случае, если разомкнутая система является устойчивой, то для того, чтобы замкнутая система тоже была такой, необходимо и достаточно, чтобы годограф системы не охватывал точку с координатами (-1;0).

2-й критерий устойчивости Найквист-Михайлова. Пусть неразомкнутая система неустойчива.

Для того, чтобы замкнутая система была устойчивой даже в случае неустойчивости разомкнутой системы, необходимо и достаточно, чтобы годограф системы охватывал точку с координатами (-1; 0) раз.

Область запаса устойчивости строится по модулю и по фазе.

Запас устойчивости по модулю – минимальное расстояние от (-1; 0) до точки пересечения годографом действительной оси.

Запас устойчивости по фазе – минимальный угол в положительном направлении между радиусом, проведённом из начала координат в точку пересечения годографом единичной окрестности, и отрицательным направлением действительной оси.

φ – запас устойчивости по фазе. Область запаса устойчивости:

Годограф устойчивости системы не должен попадать в область запаса устойчивости.

Лекция 06

Корректирующие звенья.

Корректирующие звенья ставятся в соединения с последовательной связью, параллельной связью и с обратной связью.

Пример.

Дано:

Найти: W_k.

Решение:

Влияние обратной связи на качество выполнения

Звенья:

1. Апериодическое звено.

Где – коэффициент усиления K, – период колебаний T.

Охватим элемент отрицательной обратной связью.

Пусть (усилитель).

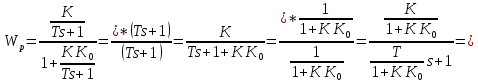
Где , .

Введение обратной связи не изменяет структуры элемента, но увеличивает его быстродействие.

2. Колебательное звено.

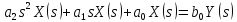
Пусть .

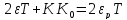
Введение обратной связи не изменяет структуры элемента, но увеличивает декремент затухания, то есть ускоряет затухание элемента.

Пример. Пусть было W_Э – эталонная:

Найдём ∆X.

– если нет обратной связи.

Охватим обратной связью:

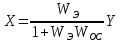
Внесение обратной связи не изменяет структуру элемента, но уменьшает погрешность измерений, вызванную изменениями параметра элемента.

Если нет обратной связи, то изменение K приведёт к тому, что погрешность ошибки (для разомкнутого случая).

Если система замкнута обратной связью и, полагая, что , то:

Если и и , то . В замкнутой:

Внесение обратной связи уменьшает относительную ошибку системы.