Лекция 01

Предмет или процесс, подлежащий изучению, мы будем называть объектом, а все предметы, взаимодействующие с нашим объектом – внешней средой. Объект будем описывать в виде некоторой системы. Система – набор элементов, находящихся в определённой связи между собой. Элемент обозначается так:

У объекта есть математическая модель, а у внешней среды её нет.

Например, блок наведения ракеты на цель (БНРнЦ):

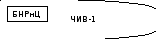
Объект нужен, чтобы им управлять.

Предмет или производственный процесс, нуждающийся в определённого рода управлении, будем называть объектом управления. Задача управления – изменять протекающие в объекте процессы так, чтобы была достигнута цель управления.

Совокупность объекта и исполняющего устройства, взаимодействие которых приводит к достижению поставленных целей, называется системой автоматического управления. Её обобщённая схема:

Но есть и более частная схема:

Принципы:

1. Принцип разомкнутого управления.

2. Принцип компенсации.

3. Принцип обратной связи.

Устойчивость – если на вход идёт воздействие, система может повести себя двояко:

а) система работает непонятно и называется неустойчивой;

б) система перешла в конкретное состояние – устойчивое.

Система бывает статической и астатической. Если система при обработке различных внешних воздействий переходит в различные состояния, то она называется статически-устойчивой, а если при воздействиях переходит в одно и то же состояние, то она называется астатически-устойчивой.

Все уравнения делятся на такие:

1. Система автоматического управления.

2. Дискретные системы – описываются разностными уравнениями.

3. Непрерывные системы – описываются дифференциальными уравнениями.

4. Смешанные системы.

5. Стационарные системы – с постоянными коэффициентами.

6. Нестационарные системы – с переменными коэффициентами.

7. Сосредоточенные системы.

8. Распределённые системы.

Лекция 02

x(t) – множество, удовлетворяющее условиям:

1. при t<0;

2. Если существует C и M такие, что: и ;

3. Имеющие счётное количество точек разрыва первого рода на интервале от 0 до ∞.

называется пространством оригиналов.

Преобразование , где , , называется преобразованием Лапласа. Обозначение: или: .

Преобразованием Лапласа присущи свойства:

1. 

2. 

…

t – это оригинал, s – это изображение.

3. 

Предполагается, что .

Применим к левой и правой части преобразование Лапласа:

Группируем:

Выразим X через Y:

Пусть при будет .

Отношение преобразования Лапласа выхода системы к преобразованию Лапласа входа системы при нулевых начальных условиях называется передаточной функцией системы и обозначается W(s):

Это основная характеристика системы, определяющая её свойства.

Значения s_i корней, при которых передаточная функция обращается в ноль, называются нулями системы. Значения s_i корней, при которых передаточная функция обращается в бесконечность, называются полюсами системы. В системе возможны до m нулей и n полюсов.

Элементы могут быть соединены последовательно, параллельно и при помощи обратной связи. Посчитаем передаточную функцию системы в целом при этих соединениях.

Последовательное соединение элементов:

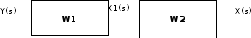
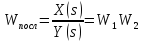
В общем виде для n элементов: .

Параллельное соединение элементов:

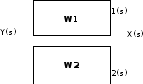
В общем виде для n элементов: .

Соединение элементов при помощи обратной связи:

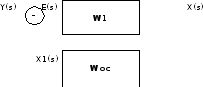
E(s) – преобразование ошибки (передаточная функция ошибки).

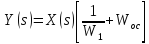
В общем виде передаточная функция системы в целом: .

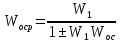Найдём передаточную функцию ошибки при соединении с обратной связью:

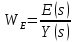
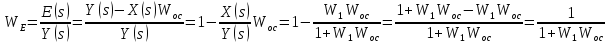
В общем виде передаточная функция ошибки: ­­­­.