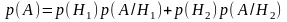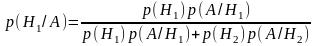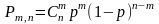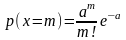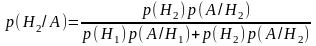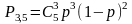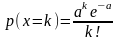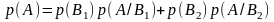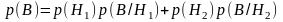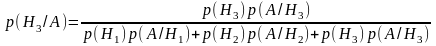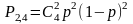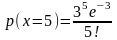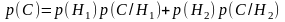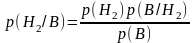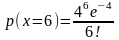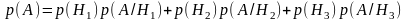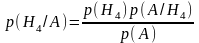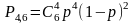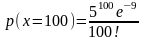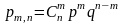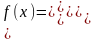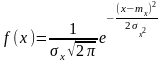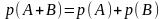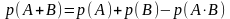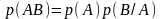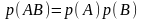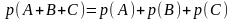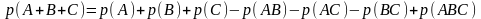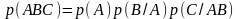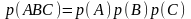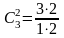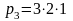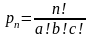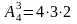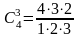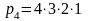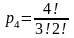307. Задание {{ 405 }} тз № 32а

Монета подбрасывается 2 раза. Составить закон распределения случайной величины - числа появления орла.



X	0	1	2
p	1/4	1/4	1/2



X	1	2
p	1/2	1/4



X	1	2
p	1/2	½



X	0	1	2
p	1/4	1/2	1/4

308. Задание {{ 406 }} ТЗ № 33а

Дан закон распределения дискретной случайной величины:

X	1	2	3
p	0,4	0,1	0,5

Найти математическое ожидание.

 MX=2,4

 MX=2,1

 MX=1,8

 MX=2,3

309. Задание {{ 407 }} ТЗ № 34а

Дан закон распределения дискретной случайной величины:

X	2	4	6
p	0,3	0,1	P3

Найти p₃ и MX.

 p₃=0,6; MX=7,6

 p₃=0,7; MX=2,7

 p₃=0,6; MX=4,6

 p₃=0,8; MX=4

310. Задание {{ 408 }} ТЗ № 35а

Случайная дискретная величина принимает три возможных значения: x₁=4 с вероятностью p₁=0.5; x₂=6 с вероятностью p₂=0.3 и x₃ с вероятностью p₃. Найти x₃ и p₃, зная, что MX=8.

 x₃=20; p₃=0,2

 x₃=18; p₃=0,1

 x₃=21; p₃=0,2

 x₃=20; p₃=0,3

311. Задание {{ 409 }} ТЗ № 40

Даны законы распределения дискретной случайной величины:

а)

X	0	1	2
p	0,1	0,2	0,3

б)

X	1	2	3
p	0,2	0,4	0,3

.

в)

X	-3	5	8
p	0,5	0,1	0,4

Какие из них составлены верно?

 а,б

 а,в

 б

 в

ЧЕТЫРНАДЦАТОЕ ЗАДАНИЕ

Непрерывная сл. Величина

321. Задание {{ 926 }} ТЗ № 84

Случайная величина x задана плотностью распределения f(x)=2x в интервале (0;1).

Вне этого интервала f(x)=0. Найти математическое

ожидание величины x.

 2/3

 3/4

 4/5

 5/6

322. Задание {{ 931 }} ТЗ № 85

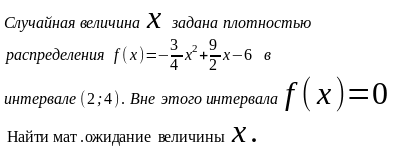
 3

 4

 5

 6

Определение мат. Ожидания и дисперсии по закону распределения

323. Задание {{ 410 }} ТЗ № 8

Если график функции распределения случайной величины X имеет вид

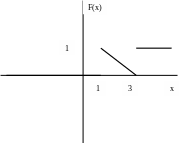
то M(2X-1) равно ….

 1/2

 1

 3

 ¾

324. Задание {{ 411 }} ТЗ № 13

Если график функции распределения случайной величины X имеет вид

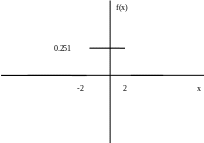
то D(2X+3) равно ….

 0

 16/3

 8/3

 4/3

325. Задание {{ 412 }} ТЗ № 18

Если случайная величина X задана плотностью распределения f(x)=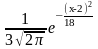 , то M(2X+1) равно ….

 1

 2

 5

 3

326. Задание {{ 413 }} ТЗ № 23

Если случайная величина X задана плотностью распределения f(x)= , то D(2X+1) равно ….

 36

 9

 18

 4

327. Задание {{ 414 }} ТЗ № 43

Если график функции распределения случайной величины X имеет вид

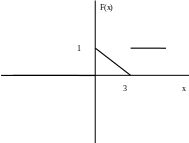
то M(2X+3) равно ….

 3/2

 1/3

 6

 3

328. Задание {{ 415 }} ТЗ № 53

Если график функции распределения случайной величины X имеет вид

то D(2X+3) равно ….

 0

 16/3

 1/3

 5

329. Задание {{ 416 }} ТЗ № 36

Дан закон распределения дискретной случайной величины

X	1	2	3	4
p	0,2	0,4	0,1	0,3

Найти P(X<3)

 P(X<3)=0,6

 P(X<3)=0,4

 P(X<3)=0,2

 P(X<3)=0

330. Задание {{ 417 }} ТЗ № 37

Дан закон распределения дискретной случайной величины X:

X	1	3	5	7
p	0,3	0,1	0,2	p4

Найти p₄ и P(X<7)

 p₄=0,5; P(X<7)=0,4

 p₄=0,4; P(X<7)=0,3

 p₄=0,3; P(X<7)=0,6

 p₄=0,4; P(X<7)=0,6

331. Задание {{ 418 }} ТЗ № 41

Дана плотность вероятности непрерывной случайной величины:

f(x)= .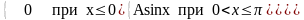

Тогда А равно:

 A=1

 A=2

 A=

 A= -

332. Задание {{ 419 }} ТЗ № 42

Дана плотность вероятности непрерывной случайной величины:

f(x)= ;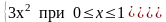

MX равно:

 X=0,75

 MX=0,6

 MX=0,75

 MX=0,78

333. Задание {{ 420 }} ТЗ № 43a

Дана плотность вероятности непрерывной случайной величины X:

f(x)= ;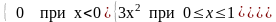

P(0,1<X<0,3) равна:

 P(0,1<X<0,3)=0,026

 P(0,1<X<0,3)=0,25

 P(0,1<X<0,3)=0,26

 P(0,1<X<0,3)=0,03

334. Задание {{ 421 }} ТЗ № 44

Дисперсия случайной величины X, заданной функцией распределения

F(x)=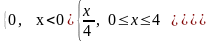

равна:

 DX=2/3

 DX=1/3

 DX=4/3

 DX=1

335. Задание {{ 422 }} ТЗ № 45

Дана плотность вероятности непрерывной случайной величины X:

f(x)= .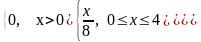

Вероятность P(1<X<3) равна:

 P(1<X<3)=0,6

 P(1<X<3)=0,55

 P(1<X<3)=0,5

 P(1<X<3)=0,4

336. Задание {{ 423 }} ТЗ № 46

Дана плотность вероятности случайной величины X:

f(x)= .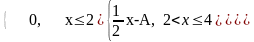

Величина А равна:

 A=1

 A=1/2

 A=2

 A=3/2

337. Задание {{ 424 }} ТЗ № 47

Дана функция распределения случайной величины

F(x)= .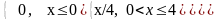

Математическое ожидание X равно:

 1

 3

 2

 2,5

338. Задание {{ 425 }} ТЗ № 48

Дана плотность вероятности непрерывной случайной величины:

f(x)= .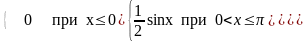

Тогда Р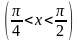 равна:

 Р =

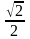
 Р =

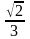
 Р =1

 Р =

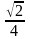
339. Задание {{ 426 }} ТЗ № 49

Дана плотность вероятности непрерывной случайной величины X:

f(x)= .

Математическое ожидание MX равно:

 MX=2

 MX=3

 MX=8/3

 MX=7/3

340. Задание {{ 427 }} ТЗ № 50

Дана интегральная функция распределения случайной величины X:

F(x)= ;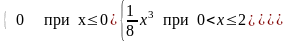

Математическое ожидание MX равно:

 MX=1/2

 MX=9/8

 MX=7/8

 MX=3/2

ПЯТНАДЦАТОЕ ЗАДАНИЕ

Разное

356. Задание {{ 903 }} ТЗ № 61

Одновременно бросаются две игральные кости. Опредеделить вероятность того, что выпадет сумма очков, равная 5

 1/9

 2/9

 1/6

 1/3

357. Задание {{ 904 }} ТЗ № 62

В лотерее имеется 10 билетов, из них 5 - выигрышных.

Берем 2 билета. Какова вероятность выигрыша?

 7/9

 5/9

 7/10

 1/2

358. Задание {{ 905 }} ТЗ № 63

На 100 карточках написаны числа от 1 до 100.

Определить вероятность того, что на случайно

взятой карточке содержится цифра 5.

 0,19

 0,18

 0,17

 0,16

359. Задание {{ 906 }} ТЗ № 64

Имеются 4 машины. Вероятность того, что машина

работает в произвольный момент времени, равна 0,9.

Определить вероятность того, что в произвольный

момент времени работает хотя бы одна машина.

 0,9999

 0,999

 0,99

 0,9

360. Задание {{ 907 }} ТЗ № 65

Вероятность попадания в цель равна 0,9.

Определить вероятность того,

что при 3 выстрелах будет 3 попадания.

 0,729

 0,3

 0,99

 0,27

361. Задание {{ 908 }} ТЗ № 66

В одном ящике деталей первого сорта 30%, в другом- 40%.

Вынимается по одной детали из каждого ящика.

Определить вероятность того, что обе вынутые

детали- первого сорта.

 0,12

 0,7

 0,24

 0,35

362. Задание {{ 909 }} ТЗ № 67

Механизм состоит из 3-х деталей.

Вероятность брака при изготовлении первой

детали равна 0,008. Второй - 0,012. Третьей - 0,01.

Определить вероятность брака при изготовлении всего механизма.

 0,03

 0,00000096

 0,06

 0,004

363. Задание {{ 910 }} ТЗ № 68

На 6 карочках написаны буквы: Р, Е, М, О, Н, Т.

Из них берут 4 наугад по одной и кладут рядом

друг с другом. Какова вероятность,

что получится слово "МОРЕ"

 1/360

 1/120

 1/60

 1/720

364. Задание {{ 911 }} ТЗ № 69

На 5 карточках написаны буквы: Т, Р, М, О, Ш.

Берут их наугад по одной и кладут рядом друг

с другом. Какова вероятность,

что получится слово "ШТОРМ"?

 1/120

 1/60

 1/360

 1/720

365. Задание {{ 912 }} ТЗ № 70

На 6 кароточках написаны буквы: А, В, К, М, О, С.

Вынимают наугад одну за другой и раскладывают их

в том порядке, в каком они были вынуты.

Найти вероятность того, что на карточках

будет написано слово "МОСКВА"?

 1/720

 1/360

 1/120

 1/60

366. Задание {{ 920 }} ТЗ № 78

В семье 5 детей. Найти вероятность того, что среди них 2 мальчика.

(Вероятность рождения мальчика принять равной 0,51)

 0,31

 0,33

 0,36

 0,4

367. Задание {{ 921 }} ТЗ № 79

В семье 5 детей. Найти вероятность того, что среди них не более двух мальчиков. (Вероятность рождения мальчика принять равной 0,51)

 0,48

 0,45

 0,42

 0,4

368. Задание {{ 922 }} ТЗ № 80

В семье 5 детей. Найти вероятность того, что среди них не менее 2-х и не более 3-х мальчиков. (Вероятность рождения мальчика принять равной 0,51)

 0,62

 0,6

 0,5

 0,4

369. Задание {{ 925 }} ТЗ № 83

Случайные величины x и y - независимы. Найти дисперсию случайной величины z=3x+2y, если известно, что D(x)=5, D(y)=6.

 69

 27

 11

 5

370. Задание {{ 928 }} ТЗ № 88

Дан закон распределения дискретной случайной величины x:

x -1 0 1

p 0,4 0,2 0,4

Найти D(2x+3)

 3,2

 1,6

 0,8

 3

371. Задание {{ 929 }} ТЗ № 89

Дан закон распределения дискретной случайной величины x

x -3 -1 0 1 3

p 0,1 0,2 0,4 0,2 0,1

Найти M(2x+3)

 3

 0

 1

 5

Условная вероятность. Полная вероятность. Формула Байеса.

372. Задание {{ 913 }} ТЗ № 71

В цеху три типа автоматических станков производят

одни и те же детали. Производительность их одинакова,

но качество работы различно. Известно,

что станки 1 -го типа производят 0,94 деталей отличного качества; 2-го - 0,9; 3-го - 0,85. Все изготовленные за смену детали сложены на складе в нерассортированном виде. Определить вероятность того,

что взятая наудачу деталь окажется отличного качества,

если станков 1-го типа - 5 штук, 2-го - 3 штуки, 3-го - 2 штуки.

 0,91

 0,89

 0,87

 0,84

373. Задание {{ 914 }} ТЗ № 72

В трех ящиках находятся однотипные изделия:

в 1-м - 10 изделий, из них 3 -нестандартных,

во 2-м - 15 иделий, из них 5 -нестандартных,

в 3-м - 20 изделий, из них 6 - нестандартных.

Наудачу выбирается 1 изделие и оно оказалось нестандартное.

Определить вероятность того, что взятое изделие принадлежало 2-му ящику.

 5/14

 2/11

 3/8

 5/7

374. Задание {{ 915 }} ТЗ № 73

Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность 1-го автомата вдвое больше производительности 2-го. Первый производит в среднем 60 % деталей отличного качества; 2-й - 84%.

Наудачу взятая из конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь произведена 1-м автоматом.

 10/17

 9/16

 8/15

 11/18

375. Задание {{ 916 }} ТЗ № 74

Вероятность удовлетворять стандарту для изделий некоторого производства равна 0,9. Предлагается упрощенноая система проверки на стандартность, дающая положительный результат с вероятностью 0,95 для изделий, удовлетворяющих стандарту, а для изделий, которые не удовлетворяют стандарту, с вероятностью 0,15. Найти вероятность того, что изделие, признанное при проверке стандартным, действительно удовлетворяет стандарту.

 0,98

 0,97

 0,96

 0,95

376. Задание {{ 917 }} ТЗ № 75

Вероятность изготовления на автоматическом станке стандартной детали равна 0.9. Определить вероятность того, что из 6 наудачу взятых деталей, 4- окажутся стандартными.

 0,0984

 0,0972

 0,0968

 0,0942

Формула Бернулли

377. Задание {{ 380 }} ТЗ № 32

Монету подбрасывают 8 раз.

Вероятность того, что 6 раз выпадет герб, равна ...

 1/8

 1/4

 7/64

 8/64

378. Задание {{ 381 }} ТЗ № 303

Монету подбрасывают 10 раз. Вероятность того, что герб выпадет хотя бы один раз, равна ...

 1023/1024

 9/10

 980/1000

 99/100

379. Задание {{ 382 }} ТЗ № 304

Игральную кость подбрасывают 4 раза. Вероятность того, что шестерка выпадет 2 раза, равна ...

 25/216

 1/2

 1/6

 18/144

380. Задание {{ 383 }} ТЗ № 305

Игральную кость подбрасывают 4 раза. Вероятность того, что шестерка выпадет хотя бы 1 раз, равна ...

 0,51

 0,25

 0,75

 0,49

381. Задание {{ 384 }} ТЗ № 306

Игральную кость подбрасывают 4 раза. Вероятность того, что шестерка выпадет не более одного раза, равна ...

 0,64

 0,87

 0,48

 0,39

382. Задание {{ 385 }} ТЗ № 23

Вероятность рождения мальчика равна 0,51. Тогда вероятность того, что среди 100 новорожденных окажется 50 мальчиков, вычисляется по формуле

 P=(1–0,51)⁵⁰·0,51

 P=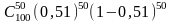

 P=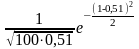

 P=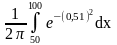

383. Задание {{ 386 }} ТЗ № 24

Монету бросают 5 раз. Вероятность того, что “герб” выпадет менее двух раз, равна (здесь P_n(m) — вероятность того, что в n испытаниях событие наступит m раз)



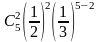
 1–(P₅(3)+P₅(4)+P₅(5))





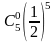
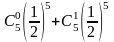
384. Задание {{ 387 }} ТЗ № 26

Монету подбрасывают 8 раз. Вероятность того, что она 6 раз упадет "гербом" вверх, равна

 6/8





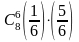
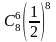
 1–

385. Задание {{ 388 }} ТЗ № 27

Вероятность выигрыша по одному лотерейному билету равна 1/7. Тогда вероятность того, что лицо, имеющее шесть билетов, выиграет по двум билетам, равна





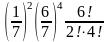
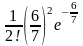
 4/7



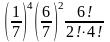
386. Задание {{ 389 }} ТЗ № 28

В партии очень большого объема имеется 95% небракованных изделий. В этом случае вероятность того, что среди взятых на испытание пяти изделий окажется более двух бракованных, равна

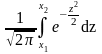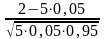 ; x₁= ; x₂=



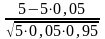
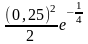
 1-((0,95)⁵+0,05·(0,95)⁴·5+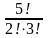 (0,05)²·(0,95)³)

 1-((0,05)⁵+0,95·(0,05)⁴·5)

387. Задание {{ 390 }} ТЗ № 12

Формула Байеса вычисления условной вероятности имеет вид





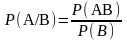
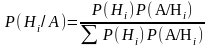
 P(B/A)=∑P(H_i/A)P(B/H_iA)

 P(A/B)=P(A)

388. Задание {{ 391 }} ТЗ № 21

Имеются три одинаковых урны. В первой 2 белых и 3 черных шара, во второй - 4 белых и 1 черный шар, в третьей - 3 белых шара. Экспериментатор подходит к одной из урн и вынимает шар. Вероятность того, что это белых шар, равна









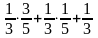
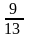
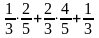
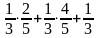
389. Задание {{ 918 }} ТЗ № 76

Два равносильных шахматиста играют в шахматы. Чему равна вероятность выиграть 2 партии из 4-х? Ничьи во внимание не принимаются.

 3/8

 1/2

 5/8

 5/16

390. Задание {{ 919 }} ТЗ № 77

Два равносильных шахматиста играют в шахматы.

Чему равна вероятность выиграть 3 партии из 6-х?

Ничьи во внимание не принимаются.

 5/16

 3/8

 1/2

 5/8

ШЕСТНАДЦАТОЕ ЗАДАНИЕ

Теория

Законы распределения

391. Задание {{ 453 }} ТЗ № 285

Биноминальный закон распределения дискретной случайной величины









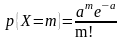
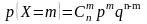
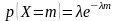
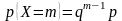
392. Задание {{ 454 }} ТЗ № 286

Распределение Пуассона дискретной случайной величины ….









393. Задание {{ 455 }} ТЗ № 287

Геометрическое распределение дискретной случайной величины ….









394. Задание {{ 456 }} ТЗ № 288

Равномерный закон распределения непрерывной случайной величины….









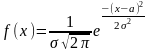
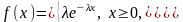
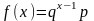
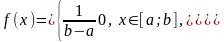
395. Задание {{ 457 }} ТЗ № 289

Показательный закон распределения непрерывной случайной величины…









396. Задание {{ 458 }} ТЗ № 290

Нормальный закон распределения непрерывной случайной величины…









397. Задание {{ 459 }} ТЗ № 291

Нормальный закон распределения непрерывной случайной величины…









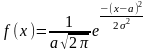
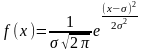
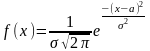
398. Задание {{ 460 }} ТЗ № 292

Нормальный закон распределения непрерывной случайной величины…









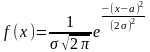
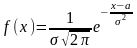
399. Задание {{ 461 }} ТЗ № 14

Формула Бернулли для вычисления вероятности того, что событие А в серии из n испытаний появится m раз, имеет вид

 P_n(m)=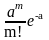

 P_n(m)=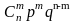

 P_n(m)=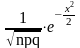

 P_n(m)= .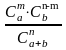

400. Задание {{ 462 }} ТЗ № 16

Точную вероятность появления события m раз в серии из n испытаний дает формула

 Бернулли P_n(m)=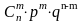

 Пуассона

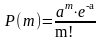
 Муавра-Лапласа P_n(m)=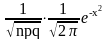

 P(m)=q^m-1·p

401. Задание {{ 463 }} ТЗ № 19

Формула Пуассона для вычисления вероятности того, что в n независимых испытаниях событие А произойдет m раз, имеет вид



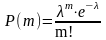
 P_n(m)=

 P_n(m)=

 P_n(m)=q^m-1·p

402. Задание {{ 464 }} ТЗ № 20

Если при вычислении вероятности того, что в серии из n независимых испытаний событие А произойдет m раз, известно, что вероятность p события А в каждом испытании мала, и число испытаний n велико, то лучше использовать формулу

 Бернулли

 сложения вероятностей

 Пуассона

 Муавра-Лапласа

403. Задание {{ 465 }} ТЗ № 61

Случайная величина 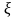распределена по закону Бернулли с параметрами 8 и 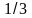. Тогда для нее справедливо равенство:









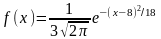
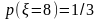
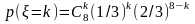
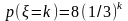
404. Задание {{ 466 }} ТЗ № 63

Случайная величина распределена по нормальному закону с параметрами 3 и 5. Тогда для нее справедливо равенство:









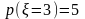
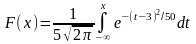
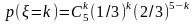
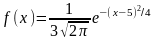
405. Задание {{ 467 }} ТЗ № 64

Случайная величина распределена по равномерному закону на отрезке 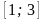. Тогда для нее справедливо равенство:









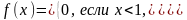
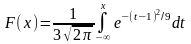
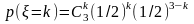
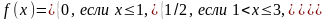
406. Задание {{ 468 }} ТЗ № 65

Случайная величина распределена по биноминальному закону с параметрами 7 и 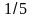. Тогда для нее справедливо равенство:









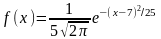
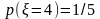
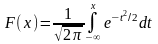
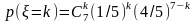
407. Задание {{ 469 }} ТЗ № 66

Случайная величина распределена по нормальному закону с параметрами 0 и 3. Тогда для нее справедливо равенство:









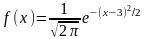
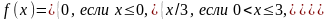
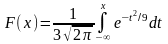
СЕМНАДЦАТОЕ ЗАДАНИЕ

Основные определения

408. Задание {{ 470 }} ТЗ № 238

Введите пропущенное слово

Случайное событие называется ….. , если оно обязательно наступит в результате проведения опыта

Правильные варианты ответа: достоверн#$#;

409. Задание {{ 471 }} ТЗ № 239

Введите пропущенное слово

Случайное событие называется ….. , если оно заведомо не произойдет в результате проведения опыта

Правильные варианты ответа: невозмож#$#;

410. Задание {{ 472 }} ТЗ № 240

Введите пропущенное слово

Два события называются …., если появление одного из них исключает появление другого события в одном и том же опыте

Правильные варианты ответа: несовмес#$#; не совмес#$#;

411. Задание {{ 473 }} ТЗ № 241

Введите пропущенное слово

Событие C , состоящее в наступлении хотя бы одного из событий A или B, называется ….. событий A и B

Правильные варианты ответа: сум#$#; объедин#$#;

412. Задание {{ 474 }} ТЗ № 242

Введите пропущенное слово

Событие C , состоящее в совместном наступлении событий A и B, называется ….. событий A и B

Правильные варианты ответа: произвед#$#; пересеч#$#;

413. Задание {{ 475 }} ТЗ № 243

Введите пропущенное слово

Отношение числа равновозможных исходов испытания, благоприятствующих событию A, к общему числу равновозможных исходов, называется …. события A

Правильные варианты ответа: вероятнос#$#;

414. Задание {{ 476 }} ТЗ № 244

Введите пропущенное слово

Два события называются ….., если появление одного из них не меняет вероятность появления другого

Правильные варианты ответа: независим#$#; не зависим#$#;

415. Задание {{ 477 }} ТЗ № 245

Введите пропущенное слово или словосочетание

Говорят, что события 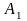, ,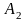…, 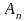образуют ….. , есл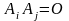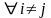и , и

Правильные варианты ответа: полн** груп#$#;

416. Задание {{ 478 }} ТЗ № 246

Введите пропущенное слово или словосочетание

Равенство 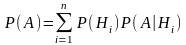в теории вероятностей называется формулой…..

Правильные варианты ответа: полн** вероятн#$#; средн** вероятн#$#;

417. Задание {{ 479 }} ТЗ № 247

Введите пропущенное слово

Равенство 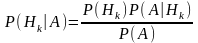в теории вероятностей называется формулой…..

Правильные варианты ответа: Байе#$#; Бей#$#; Бай#$#;

418. Задание {{ 480 }} ТЗ № 248

Введите пропущенное слово

Равенство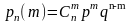 в теории вероятностей называется формулой…..

Правильные варианты ответа: Бернул#$#;

419. Задание {{ 481 }} ТЗ № 1

Величина вероятности события лежит в пределах

 от 0% до 100%

 от –π до π (π=3,14)

 от –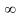 до

 от 0 до 1

420. Задание {{ 482 }} ТЗ № 2

Бросается игральный кубик с шестью гранями. Событие А=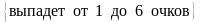

 невозможное

 случайное

 достоверное

 редкое

421. Задание {{ 483 }} ТЗ № 3

Статистическая вероятность событий - это

 среднее арифметическое вероятностей событий в серии испытаний

 сумма вероятностей события в серии испытаний

 отношение числа появления события А к общему числу произведенных опытов

 число появления события в серии испытаний

422. Задание {{ 484 }} ТЗ № 4

Бросаются два игральных кубика. Событие С=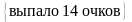

 достоверное

 возможное

 маловероятное

 невозможное

423. Задание {{ 485 }} ТЗ № 7

Произведение двух событий - это

 произведение вероятностей этих событий

 меры возможности одновременного появления этих событий

 событие, состоящее в одновременном появлении этих событий

 событие, состоящее в появлении одного или другого события

424. Задание {{ 486 }} ТЗ № 13

Опыты называются независимыми, если

 вероятность того или иного исхода каждого опыта не зависит от того, какие исходы имели другие опыты

 условия опыта не зависят от внешних факторов

 они проводятся в одинаковых условиях

 они имеют одинаковую вероятность

425. Задание {{ 487 }} ТЗ № 15

Число m₀ наступления события в серии из n испытаний называется наивероятнейшим числом, если

 это число является наибольшим среди всех остальных

 оно совпадает с числом испытаний n

 оно соответствует наибольшей вероятности в данной серии испытаний

 событие, соответствующее этому числу, достоверно

426. Задание {{ 488 }} ТЗ № 17

Локальная теорема Муавра-Лапласа вычисляет вероятность наступления события m раз в n испытаниях с большей точностью, если

 n близка к нулю





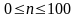
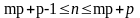
 n достаточно велико

427. Задание {{ 489 }} ТЗ № 18

Следующая функция называется функцией Лапласа









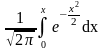
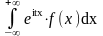
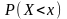
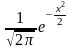
ВОСЕМНАДЦАТОЕ ЗАДАНИЕ

Свойства плотности вероятности и функции распределения

428. Задание {{ 490 }} ТЗ № 279

Выберите все верные варианты

Плотность распределения вероятности непрерывной случайной величины 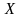обладает свойствами ….









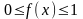
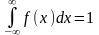
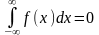
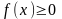
429. Задание {{ 491 }} ТЗ № 280

Плотность распределения вероятности непрерывной случайной величины обладает свойствами ….









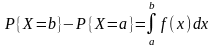
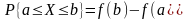
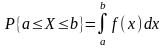
430. Задание {{ 492 }} ТЗ № 281

Выберите все верные варианты

Плотность распределения вероятности непрерывной случайной величины обладает свойствами ….







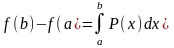
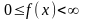
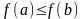 , если

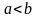
431. Задание {{ 493 }} ТЗ № 282

Выберите все верные варианты

Функция распределения 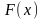непрерывной случайной величины обладает свойствами ….







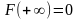
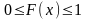
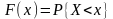
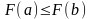 , если

432. Задание {{ 494 }} ТЗ № 283

Выбериет все верные варианты

Функция распределения непрерывной случайной величины обладает свойствами ….



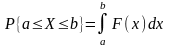
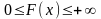 ТОЖЕ ВЕРНЫЙ ОТВЕТ!!!!!





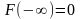
433. Задание {{ 495 }} ТЗ № 284

Выберите все верные варианты

Функция распределения непрерывной случайной величины обладает свойствами ….









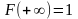
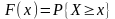
ДЕВЯТНАДЦАТОЕ ЗАДАНИЕ

Соответствие межу формулой и названием

434. Задание {{ 13 }} ТЗ № 91

Установить соответствие между формулой и ее названием

Формула полной вероятности
Формула Байеса
Формула Бернулли
Формула Пуассона

435. Задание {{ 14 }} ТЗ № 92

Установить соответствие между формулой ее названием

Формула Байеса
Формула Бернулли
Формула Пуассона
Формула полной вероятности

436. Задание {{ 15 }} ТЗ № 93

Установить соответствие между формулой и ее названием

Формула полной вероятности
Формула Байеса
Формула Бернулли
Формула Пуассона

437. Задание {{ 16 }} ТЗ № 94

Установить соответствие между формулой и ее названием

Формула полной вероятности
Формула Байеса
Формула Бернулли
Формула Пуассона

438. Задание {{ 17 }} ТЗ № 95

Установить соответствие между формулой и ее названием

Формула полной вероятности
Формула Байеса
Формула Бернулли
Формула Пуассона

439. Задание {{ 18 }} ТЗ № 96

Установить соответствие между формулой и названием распределения

Биномиальное распределение
Распределение Пуассона
Равномерное распределение
Нормальный закон распределения

440. Задание {{ 19 }} ТЗ № 97

Установить соответствие между формулой и ее названием

Теорема сложения вероятностей несовм-х событий
Теорема сложения вероятностей совместимых событий
Теорема умножения вероятностей
Теорема умножения вероятностей для независимых событий

441. Задание {{ 20 }} ТЗ № 98

Установить соответствие между формулой и ее названием

Теорема сложения вероятностей для несовместных событий
Теорема сложения вероятностей для совместных событий
Теорема умножения вероятностей
Теорема умножения вероятностей для независимых событий

442. Задание {{ 21 }} ТЗ № 99

Установить соответствие между формулой и ее названием

Число размещений из 3-х элементов по 2
Число сочетаний из 3-х элементов по 2
Число перестановок из 3-х элементов
Число перестановок из n элементов, если среди них имеются одинаквые

443. Задание {{ 22 }} ТЗ № 100

Установить соответствие между формулой и ее названием

Число размещений из 4-х элементов по 3
Число сочетаний из 4-х элементов по 3
Число перестановок из 4-х элементов
Число перестановок из 4-х элементов, если среди них имеются одинаковые

ДВАДЦАТОЕ ЗАДАНИЕ