Математическое ожидание и дисперсия дсв
301. Задание {{ 399 }} ТЗ № 31
Дискретная случайная величина задана рядом распределения вероятностей:
-
X
-1
2
4
P
0.1
a
b
Тогда ее математическое ожидание равно 3.3 если …..
a=0,1; b=0,9
a=0,8; b=0,1
a=0,2; b=0,7
a=0,1; b=0,8
302. Задание {{ 400 }} тз № 32
Дискретная случайная величина задана рядом распределения вероятностей:
-
X
-2
1
3
P
0.1
a
b
Тогда ее математическое ожидание равно 2.3 если …..
a=0,1; b=0,8
a=0,8; b=0,1
a=0,25; b=0,75
a=0,3; b=0,6
303. Задание {{ 401 }} тз № 33
Дискретная случайная величина задана рядом распределения вероятностей:
-
X
-1
0
3
P
0.1
0.3
0.6
Тогда математическое
ожидание случайной величины
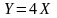равно …..
5,7
8
7,6
6,8
304. Задание {{ 402 }} тз № 34
Дискретная случайная величина задана рядом распределения вероятностей:
-
X
-2
-1
4
P
0.1
0.3
0.6
Тогда математическое
ожидание случайной величины
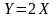равно …..
3,8
3,6
4
4,8
305. Задание {{ 403 }} тз № 35
Дискретная случайная величина задана рядом распределения вероятностей:
-
X
-1
0
3
4
P
0.1
0.1
0.1
0.7
Тогда математическое
ожидание случайной величины
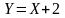равно …..
5
3
4
6
306. Задание {{ 404 }} тз № 31a
Составить закон распределения вероятностей числа попаданий в мишень при двух независимых выстрелах, если вероятность попадания при каждом выстреле равна 0,8
X |
0 |
1 |
2 |
p |
0,14 |
0,16 |
0,64 |
X |
1 |
2 |
p |
0,32 |
0,64 |
X |
0 |
1 |
2 |
p |
0,8 |
0,16 |
0,8 |
.
X |
0 |
1 |
2 |
p |
0,04 |
0,32 |
0,64 |