Вероятность работы эл. Цепи
244. Задание {{ 351 }} ТЗ № 2
Различные элементы эл. цепи работают независимо друг от друга
I---a1---I
I I
----I---a2---I-----
I I
I---a3---I
Вероятность безотказной работы элементов за время T следующие p(a1)=0.6 p(a2)=0.8 P(a3)=0.7
Тогда вероятность безотказной работы системы за время T равна…..
0.832
0.976
0.744
0.493
245. Задание {{ 352 }} тз № 7
Различные элементы эл. цепи работают независимо друг от друга
I---a1---I
I I
----I I-----
I I
I---a2---I
Вероятность безотказной работы элементов за время T следующие p(a1)=0.6 p(a2)=0.8
Тогда вероятность безотказной работы системы за время T равна…..
0,8
0,6
0,92
0,48
246. Задание {{ 353 }} тз № 12
Различные элементы эл. цепи работают независимо друг от друга
I---a1---I
I I
----I I-----a3------
I I
I---a2---I
Вероятность безотказной работы элементов за время T следующие p(a1)=0.6 p(a2)=0.8 P(a3)=0.7
Тогда вероятность безотказной работы системы за время T равна…..
0.893
0.588
0.644
0.485
247. Задание {{ 354 }} тз № 17
Различные элементы эл. цепи работают независимо друг от друга
I---a1---a2----I
I I
----I I--------
I I
I-------a2------I
Вероятность безотказной работы элементов за время T следующие p(a1)=0.6 p(a2)=0.8 P(a3)=0.7
Тогда вероятность безотказной работы системы за время T равна…..
0.742
0.821
0.426
0.844
248. Задание {{ 355 }} тз № 22
Различные элементы эл. цепи работают независимо друг от друга
I---a2---I
I I
-----a1------I I-----
I I
I---a3---I
Вероятность безотказной работы элементов за время T следующие p(a1)=0.6 p(a2)=0.8 P(a3)=0.7
Тогда вероятность безотказной работы системы за время T равна…..
0,264
0,336
0,564
0,376
249. Задание {{ 356 }} ТЗ № 10
Электрическая цепь имеет вид:
Событие Ак={элемент с номером к вышел из строя} к=1,2,3,4. Событие В={разрыв цепи} выражается через события А1, А2, А3, А4 следующим образом:
В=А1+А2+А3+А4
В=А1·А4+А2+А3
В=А1+А2·А3+А4
В=А1·А2·А3·А4
ДЕВЯТОЕ ЗАДАНИЕ
Вероятность суммы и произведения событий
250. Задание {{ 357 }} ТЗ № 41
Два стрелка производят по одному выстрелу. Вероятность попадания в цель для первого и второго стрелков равна 0,8 и 0,75 соответственно. Тогда вероятность того, что цель будет поражена, равна ...
0,55
0,40
0,95
0,60
251. Задание {{ 358 }} ТЗ № 42
Два стрелка производят по одному выстрелу. Вероятность попадания в цель для первого и второго стрелков равна 0,7 и 0,6 соответственно. Тогда вероятность того, что цель будет поражена, равна...
0,58
0,42
0,88
0,98
252. Задание {{ 359 }} ТЗ № 43
По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,4 и 0,35. Тогда вероятность банкротства обоих предприятий равна...
0,12
0,14
0,76
0,39
253. Задание {{ 360 }} ТЗ № 44
В первой урне 4 белых и 6 черных шаров. Во второй урне 1 белый и 9 черных шаров. Из наудачу взятой урны вынули 1 шар. Тогда вероятность того, что этот шар окажется белым, равна...
0,25
0,5
0,15
0,3
254. Задание {{ 361 }} ТЗ № 45
Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,7 и 0,6 соответственно. Тогда вероятность того, что цель будет поражена одной пулей, равна...
0,46
0,42
0,54
0,13
255. Задание {{ 362 }} ТЗ № 8
В урне a белых, b черных, c красных шаров. Вероятность того, что из урны вынут белый или красный шар равна
(a+c)·(a+b)
(a+b+c)/(b+c)
(a+c)/(a+b+c)
(ab)/(a+b+c)
256. Задание {{ 363 }} ТЗ № 9
В урне a белых и b черных шаров. Из урны вынимают два шара. По теореме умножения вероятностей вероятность того, что оба шара белые, равна
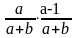
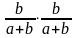
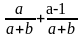
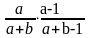
257. Задание {{ 364 }} ТЗ № 11
А, В, С - три события, наблюдаемые в эксперименте. Событие
Е = {из трех событий А, В, С произойдет ровно одно} в алгебре событий имеет следующий вид (черта над событием означает противоположное событие):
E=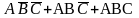
E=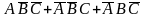
E=ABC
E=A+B+C
258. Задание {{ 365 }} ТЗ № 25
В результате многолетних наблюдений установлено, что вероятность выпадения дождя 1 октября в г. Хабаровске равна 1/7. Наивероятнейшее число m0 дождливых дней 1 октября за 40 лет лежит в пределах
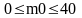
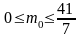
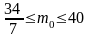
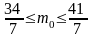
259. Задание {{ 366 }} ТЗ № 30
Вероятность того, что покупателю потребуется обувь 40-го размера, равна 0,4. Вошли трое покупателей. Тогда вероятность, что хотя бы одному из них потребуется обувь 40-го размера, равна
1–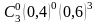
+
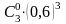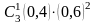
1– –
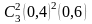
ДЕСЯТОЕ ЗАДАНИЕ