229. Задание {{ 686 }} Абс. Сходимость

Выберите правильную формулировку

Ряд называется абсолютно сходящимся, если

сходится ряд









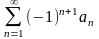
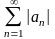
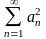
230. Задание {{ 687 }} Предельный признак сравнения

Выберете верные из приведенных ниже утверждений

Пусть даны ряды 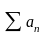и

и существует предел Тогда

 из расходимости ряда a_n следует расходимость ряда b_n

 из расходимости ряда b_n следует расходимость ряда a_n

 из сходимости ряда b_n следует сходимость ряда a_n

 из расходимости ряда a_n следует сходимость ряда b_n

 ряды a_n и b_n сходятся или расходятся одновременно

231. Задание {{ 688 }} отбрасывание членов

Выберите верный ответ

Если отбросить любое конечное число членов ряда, то

 это не повлияет на его сходимость или расходимость

 сходящийся ряд может стать расходящимся

 расходящийся ряд может стать сходящимся

 как сходящийся ряд может стать расходящимся, так и наоборот

232. Задание {{ 689 }} умножение ряда на число

Выберите верный ответ

Если все члены числового ряда умножить на одно и то же число, то

 это не повлияет на его сходимость или расходимость

 сходящийся ряд может стать расходящимся

 расходящийся ряд может стать сходящимся

 как сходящийся ряд может стать расходящимся, так и наоборот

233. Задание {{ 690 }} расходимость положительного ряда

Выберите верный ответ

Числовой ряд с положительными членами расходится. Это означает, что предел последовательности его частичных сумм

 равен бесконечности

 равен некоторому положительному числу

 не существует

 равен нулю

234. Задание {{ 691 }} геометр. прогрессия

Выберите верный ответ

Числовой ряд 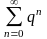сходится при

 q>1

 q<1

 |q|>1

 |q|<1

235. Задание {{ 692 }} Даламбер

Выберите верный ответ

По признаку Даламбера ряд сходится, если

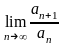
 =1

 <1

 >1

236. Задание {{ 693 }} необх. усл. выполнено

Выберите верный ответ

Если для числового ряда выполнено необходимое условие сходимости, то

 ряд сходится

 ряд расходится

 ряд может как сходиться, так и расходиться

 ряд сходится абсолютно

237. Задание {{ 694 }} Дзета-функция

Выберите верный ответ

Ряд 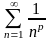сходится, если

 p=1

 p<1

 p>1

 p=0

238. Задание {{ 695 }} Из абсолютной сх. ->обычная1

Выберите верный ответ(ответы)

1) если ряд сходится абсолютно, то он сходится в обычном смысле;

2) если ряд сходится условно, то он сходится в обычном смысле;

3) если ряд сходится абсолютно, то он сходится условно;

4) если ряд сходится в обычном смысле, то он сходится условно;

 1)

 2)

 3)

 4)

 5)

239. Задание {{ 696 }} Из абсолютн. сх. ->обычная2

Выберите верный ответ (ответы)

Даны числовые ряды

(1)

и

. (2)

Тогда

 из сходимости (1) следует сходимость (2)

 из сходимости (2) следует сходимость (1)

 ряды сходятся или расходятся одновременно

 из сходимости (2) не следует сходимость (1)

 из сходимости (1) не следует сходимость (2)

240. Задание {{ 697 }} подпоследовательность членов>0.001

Выберите верный ответ (ответы)

Данный ряд содержит бесконечно много членов, превосходящих число 0,001. Тогда этот ряд

 сходится

 расходится

 может как сходиться, так и расходиться

 сходится условно

 сходится абсолютно

241. Задание {{ 698 }} Необх. усл. выполнено-и что?

Выберите верный ответ (ответы)

Общий член некоторого ряда стремиться к нулю при n стремящемся к бесконечности. Тогда этот ряд

 сходится

 расходится

 сходится абсолютно

 может как сходиться, так и расходиться

242. Задание {{ 699 }} перестановка сход. ряда

Выберите верный ответ (ответы)

Если члены сходящегося ряда переставить в произвольном порядке, то полученный ряд

 может оказаться расходящимся

 может оказаться сходящимся к сумме, отличной от прежней

 будет сходиться к прежней сумме

243. Задание {{ 700 }} перестановка абс. сх. ряда

Выберите верный ответ (ответы)

Если члены абсолютно сходящегося ряда переставить в произвольном

порядке, то полученный ряд

 будет сходиться к прежней сумме

 может сходиться к сумме, отличной от прежней

 может оказаться расходящимся

ВОСЬМОЕ ЗАДАНИЕ