Формулы и определения
444. Задание {{ 748 }} Теорема умножения
Найдите вероятность события С, если
С=АВ, Р(А)=0.5, Р(В)=0.3, А и В - независимы.
Правильные варианты ответа: 0.15; 0,15;
445. Задание {{ 749 }} Теорема сложения вероятностей
Найдите вероятность события С, если
С=А+В, Р(А)=0.4, Р(В)=0.2, А и В несовместны.
Правильные варианты ответа: 0,6; 0.6;
446. Задание {{ 750 }} Теорема сложения вероятностей (совм)
Найдите вероятность события С, если
С=А+В, Р(А)=0.1, Р(В)=0.7, Р(АВ)=0.05.
Правильные варианты ответа: 0,75; 0.75;
447. Задание {{ 751 }} Теорема умножения (зависимые)
Найдите вероятность произведения событий А и В, если
Р(В)=0.2, Р(А|В)=0.3.
Правильные варианты ответа: 0.06; 0,06;
448. Задание {{ 752 }} Классическое опр-е вер-ти
Выберите правильный ответ(ответы)
Вероятность события, вычисленная в соответствии с классическим определением - это
отношение числа благоприятных исходов к общему числу элементарных исходов
отношение общего числа элементарных исходов к числу благоприятных исходов
отношение числа появлений события в серии испытаний к длине этой серии
449. Задание {{ 753 }} Несовместн_независимость
Какие из приведенных утверждений верны?
Если события А и В
несовместны, то они независимы
независимы, то они несовместны
совместны, то они зависимы
зависимы, то они совместны
совместны, то они независимы
независимы, то они совместны
несовместны, то они зависимы
450. Задание {{ 754 }} Полная группа
Выберите правльный ответ (ответы)
Если А, В, ..., С - полная группа событий, то они
попарно несовместны
попарно независимы
в сумме дают невозможное событие
в сумме дают достоверное событие
451. Задание {{ 755 }} Противоположные
Выберите верный ответ (ответы)
Если события А и В противоположны, то они
совместны
несовместны
зависимы
независимы
452. Задание {{ 756 }} Сумма событий
Выберите правильный ответ (ответы)
Сумма событий А и В - это событие, состоящее в том, что
А и В произошли одновременно
хотя бы одно из этих событий произошло
только одно из этих событий произошло
453. Задание {{ 757 }} Произведение событий
Выберите правильный ответ (ответы)
Произведение событий А и В - это событие, состоящее в том, что
только одно из этих событий произошло
они произошли одновременно
хотя бы одно из этих событий произошло
454. Задание {{ 758 }} Условная вероятность
Выберите правильный ответ (ответы)
Условная вероятность Р(А|В) равна
Р(АВ)/Р(В)
Р(АВ)/Р(А)
Р(А+В)/Р(А)
Р(А+В)/Р(В)
455. Задание {{ 759 }} Полная вероятность
Выберите правильный ответ(ответы)
Формула полной вероятности имеет вид
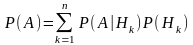
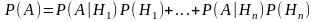
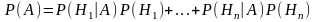
456. Задание {{ 760 }} Байес
Выберите правильный ответ(ответы)
Формула Байеса имеет вид
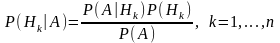
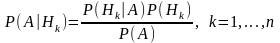
457. Задание {{ 761 }} Бернулли
Выберите верный ответ(ответы)
В серии из n испытаний по схеме Бернулли успех наступает с вероятностью р. Тогда формула Бернулли для вероятности наступления ровно k успехов имеет вид
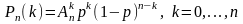
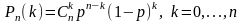
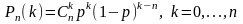
458. Задание {{ 762 }} Доля брака
Выберите правильный ответ (ответы)
В партии, состоящей из n деталей, m деталей бракованные. Для контроля качества выбирают пробную партию, состоящую из k деталей. Тогда вероятность того, что среди них окажется ровно r бракованных, равна
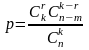
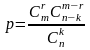
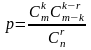
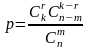
459. Задание {{ 763 }} Плотность и функция распр
Выберите правильный ответ (ответы)
Пусть F(x) - функция распределения непрерывной случайной величины, p(x) - ее плотность вероятности. Тогда
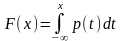
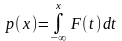
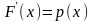
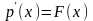
460. Задание {{ 764 }} Свойства плотности
Выберите правильный ответ (ответы)
Пусть р(х) - плотность вероятности. Тогда функция р(х)
не убывает
не возрастает
неотрицательна
не превосходит единицы
возрастает
убывает
461. Задание {{ 765 }} Свойства функции распр
Выберите правильный ответ (ответы)
Пусть F(x) - функция распределения. Тогда F(x)
возрастает
убывает
не превосходит единицы
не возрастает
не убывает
неотрицательна
462. Задание {{ 766 }} Смысл мат ожидания
Выберите правильный ответ (ответы)
Математическое ожидание случайной величины - это
ее среднее значение
мера ее рассеяния
ее наибольшее значение
ее наименьшее значение
мера ее отклонения от среднего значения
463. Задание {{ 767 }} Смысл дисперсии
Выберите правильный ответ (ответы)
Дисперсия случайной величины - это
ее среднее значение
мера ее рассеяния
ее наибольшее значение
ее наименьшее значение
464. Задание {{ 768 }} Малая дисперсия
Выберите правильный ответ (ответы)
Дисперсия некоторой случайной величины мала. Тогда
ее значения группируются вблизи среднего значения
ее значения сильно разбросаны относительно среднего значения
ее среднее значение велико
ее среднее значение мало
465. Задание {{ 769 }} Равномерн. распр.1
Случайная величина равномерно распределена на отрезке [0,1].
Тогда значение ее плотности вероятности p(x) на этом отрезке равно
Правильные варианты ответа: 1;
466. Задание {{ 770 }} Равномерн. распр.2
Случайная величина равномерно распределена на отрезке [-1/2;0].
Тогда значение ее плотности вероятности p(x) на этом отрезке равно
Правильные варианты ответа: 2;
467. Задание {{ 771 }} Равномерн. распр.3
Случайная величина равномерно распределена на отрезке [0;1/3].
Тогда значение ее плотности вероятности p(x) на этом отрезке равно
Правильные варианты ответа: 3;
468. Задание {{ 772 }} Равномерн. распр.4
Выберите правильный ответ (ответы)
Случайная величина равномерно распределена на отрезке [0;1/4]. Тогда значение ее плотности вероятности p(x) на этом отрезке равно
Правильные варианты ответа: 4;
469. Задание {{ 773 }} Равномерн. распр.5
Случайная величина равномерно распределена на отрезке [-1/2;1/2].
Тогда значение ее плотности вероятности p(x) на этом отрезке равно
Правильные варианты ответа: 1;
470. Задание {{ 774 }} Норм. распр.1
Некоторая случайная величина имеет плотность вероятности вида
Чему равно ее математическое ожидание?
Правильные варианты ответа: 1;
471. Задание {{ 775 }} Норм. распр.2
Некоторая случайная величина имеет плотность вероятности вида
Чему равно ее математическое ожидание?
Правильные варианты ответа: 2;
472. Задание {{ 776 }} Норм. распр.3
Некоторая случайная величина имеет плотность вероятности вида
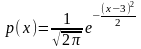
Чему равно ее математическое ожидание?
Правильные варианты ответа: 3;
473. Задание {{ 777 }} Норм. распр.4
Некоторая случайная величина имеет плотность вероятности вида
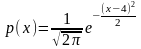
Чему равно ее математическое ожидание?
Правильные варианты ответа: 4;
474. Задание {{ 778 }} Норм. распр.5
Некоторая случайная величина имеет плотность вероятности вида
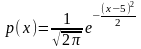
Чему равно ее математическое ожидание?
Правильные варианты ответа: 5;
475. Задание {{ 779 }} Норм. распр. дисп.1
Некоторая случайная величина имеет плотность вероятности вида
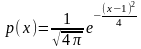
Чему равна ее дисперсия?
Правильные варианты ответа: 2;
476. Задание {{ 780 }} Норм. распр. дисп.2
Некоторая случайная величина имеет плотность вероятности вида
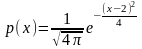
Чему равна ее дисперсия?
Правильные варианты ответа: 2;
477. Задание {{ 781 }} Норм. распр. дисп.3
Некоторая случайная величина имеет плотность вероятности вида
Чему равна ее дисперсия?
Правильные варианты ответа: 2;
478. Задание {{ 782 }} Норм. распр. дисп.4
Некоторая случайная величина имеет плотность вероятности вида
Чему равна ее дисперсия?
Правильные варианты ответа: 2;
479. Задание {{ 783 }} Норм. распр. дисп. 5
Некоторая случайная величина имеет плотность вероятности вида
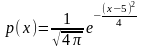
Чему равна ее дисперсия?
Правильные варианты ответа: 2;