
- •Часть 1.Численое интегрирование.
- •Формулы прямоугольников
- •Формула трапеций
- •Часть 2.Численые методы решения задачи Коши для оду.
- •Приближенные методы решения задачи Коши для оду первого порядка
- •Метод Эйлера
- •Модифицированный метод Эйлера
- •Часть 3.Численые методы решения краевой задачи для оду 2-го порядка. Постановка задачи
- •Аппроксимация производных
Новосибирский Государственный Архитектурно-Строительный Университет (Сибстрин)
Кафедра прикладной математики
Лабораторная работа 4.
Численное интегрирование.
Численные методы решения ОДУ.
В-9
Выполнил Лосев Е.А.
Группа 323
Проверила Соловьева С.И.
Новосибирск 2012
Часть 1.Численое интегрирование.
Постановка задачи
Требуется
найти значение определенного интеграла
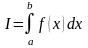 для некоторой заданной на отрезке
для некоторой заданной на отрезке
 функции
функции
 .
Для некоторых функций значение интеграла
можно найти точно. Однако в общем случае
значение интеграла можно найти только
приближенно, используя тот или иной
способ численного интегрирования.
.
Для некоторых функций значение интеграла
можно найти точно. Однако в общем случае
значение интеграла можно найти только
приближенно, используя тот или иной
способ численного интегрирования.
Численное
интегрирование основано на замене
интеграла некой суммой
 .
Такая замена следует из определения
интеграла как предела суммы
.
Такая замена следует из определения
интеграла как предела суммы
 .
Зафиксировав
.
Зафиксировав
 ,
мы получим предыдущую сумму.
,
мы получим предыдущую сумму.
Приближенное
равенство
 называется квадратурной
формулой,
называется квадратурной
формулой,
 –
узлами,
а
–
узлами,
а
 - коэффициентами
квадратурной
формулы. Разность
- коэффициентами
квадратурной
формулы. Разность
 называется погрешностью
квадратурной
формулы.
называется погрешностью
квадратурной
формулы.
Разобьем
отрезок
на
равных частей точками
 .
Получим равномерную сетку:
.
Получим равномерную сетку:
 .
Тогда
.
Тогда
 .
.
Для
построения квадратурной формулы на
всем отрезке
достаточно построить квадратурную
формулу на частичном отрезке
 .
.
Методы решения
Формулы прямоугольников
Пусть
 ,
т.е. мы аппроксимируем
левой кусочно-постоянной интерполяцией.
Тогда получим
,
т.е. мы аппроксимируем
левой кусочно-постоянной интерполяцией.
Тогда получим
 .
.
Таким
образом,
 .
Эта формула называется формулой левых
прямоугольников.
.
Эта формула называется формулой левых
прямоугольников.

Рис. 4.1. Метод левых прямоугольников
Геометрическая интерпретация метода левых прямоугольников представлена на рис. 4.1, который показывает, что точное значение интеграла (площадь криволинейной области под графиком ) заменяется на сумму площадей прямоугольников, построенных под кусочно-постоянной интерполирующей функцией.
Аналогично
может быть получена формула
правых прямоугольников.
Здесь
 .
В результате получим:
.
В результате получим:
 .
.

Рис. 4.2. Метод правых прямоугольников
Оценим погрешность формулы левых прямоугольников:
 .
.
Воспользуемся формулой Тейлора:
 .
.
Тогда
 Пусть
Пусть
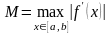 ,
тогда
,
тогда
 ,
т.е. формула левых прямоугольников
имеет первый
по
,
т.е. формула левых прямоугольников
имеет первый
по
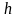 порядок точности.
Аналогичную оценку можно получить для
формулы правых прямоугольников.
порядок точности.
Аналогичную оценку можно получить для
формулы правых прямоугольников.
Если
на каждом отрезке
заменить значение функции f(x)
на ее значение в середине отрезка, т.е.
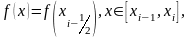 получим формулу
средних прямоугольников:
получим формулу
средних прямоугольников:
 .
.
Если
функция
задана таблично, среднее значение на
локальном отрезке можно вычислить с
помощью линейной интерполяции
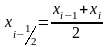 ,
и тогда метод средних имеет вид:
,
и тогда метод средних имеет вид:

Для оценки погрешности метода
 .
.
воспользуемся формулой Тейлора:
 .
.
Тогда
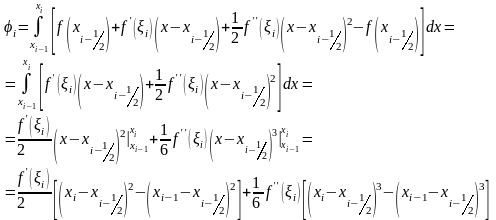 Поскольку
Поскольку
 и
и
 ,
то
,
то

Пусть
 ,
тогда
,
тогда
 ,
т.е.
формула средних прямоугольников имеет
второй
порядок точности.
,
т.е.
формула средних прямоугольников имеет
второй
порядок точности.
Формула трапеций
Во всех рассмотренных формулах площадь криволинейной трапеции заменялась на площадь прямоугольников.
В
методе трапеций криволинейная трапеция
заменяется на прямоугольную (рис. 4.3),
площадь которой вычисляется по известным
формулам:
 .
.

Рис. 4.3. Метод трапеций
Формула трапеций может быть также получена путем замены подынтегральной функции интерполяционным полиномом первой степени:
 .
.
Действительно
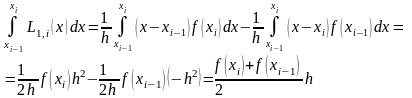 .
.
Тогда для всего отрезка получим:
 .
.
Можно показать, что формула трапеций совпадает с формулой средних для таблично заданной функции и также имеет второй порядок точности.
Формулу трапеций можно также записать в виде:
 .
.
Решение
Задана
исходная функция
 и интервал [-1;1],
и интервал [-1;1],
 ,
,
 =0,1..N,
h=(b-a)/N.
=0,1..N,
h=(b-a)/N.
1.Вычислим точное значение интеграла
 2,718282-0,367879=2,350402
2,718282-0,367879=2,350402
2.Вычисление с помощью метода прямоугольников и трапеции
При N=10 h=0,2

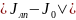 =0,22721
=0,22721
 =0,24287
=0,24287
 =0,00391
=0,00391
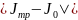 =0,00783
=0,00783
 =2,123192
=2,123192
 =2,593272
=2,593272
 =2,34649
=2,34649
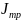 =2,358232
=2,358232
Для
нахождения интеграла методом левых
прямоугольников, необходимо просуммировать
элементы третьего ряда в диапазоне
 и умножить на шаг
и умножить на шаг
 .
Аналогично для формулы правых
прямоугольников, суммировать в диапазоне
.
Аналогично для формулы правых
прямоугольников, суммировать в диапазоне
 .
Сумма элементов пятого столбца,
помноженная на шаг, даст результат по
формуле средних прямоугольников.
Согласно формуле трапеций, необходимо
к полусумме первого и последнего
значения элементов третьего столбца
добавить сумму всех остальных членов
этого столбца, и умножить результат на
шаг
.
.
Сумма элементов пятого столбца,
помноженная на шаг, даст результат по
формуле средних прямоугольников.
Согласно формуле трапеций, необходимо
к полусумме первого и последнего
значения элементов третьего столбца
добавить сумму всех остальных членов
этого столбца, и умножить результат на
шаг
.
 -формула
левых прямоугольников,
-формула
левых прямоугольников,
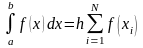 -формула
правых прямоугольников,
-формула
правых прямоугольников,
 -формула
средних прямоугольников,
-формула
средних прямоугольников,
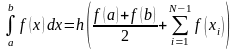 -формула
трапеции.
-формула
трапеции.
При N=20 h=0,1

=0,11556139
=0,119478849
=0,000978661
=0,00195873
=2,23484061
=2,469880849
=2,349423339
=2,35236073
Вывод:
для данной функции
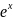 на интервале
[-1;1] наиболее точной является формула
средних прямоугольников с погрешностью
при n=10
равной 0,00391и
при n=20
равной 0,000979
на интервале
[-1;1] наиболее точной является формула
средних прямоугольников с погрешностью
при n=10
равной 0,00391и
при n=20
равной 0,000979
