BФедеральное агентство по образованию

Уральский государственный технический университет-УПИ

Имени первого Президента России Б. Н. Ельцина

Интеллектуальные информационные системы

Методические указания к выполнению лабораторных работ

для студентов всех форм и технологий обучения специальностей

Екатеринбург

УГТУ-УПИ

2010

УДК 681.3

Составители: Потанин Н.И.

Научный редактор д-р физ.-мат. наук проф.

Интеллектуальные информационные системы : методические указания к выполнению лабораторных работ для студентов специальностей

сост. Н.И. Потанин. Екатеринбург : УГТУ-УПИ, 2010. 74 с.

В методических указаниях приводится пример решения задачи с помощью пакета Квазар. Приведен порядок решения задачи в пакетах Квазар. Квазар: подготовка данных, ввод и проверка данных, решение задачи таксономии, задачи информативности признаков, задачи дискриминатнтного анализа.

Библиогр.: 4 назв. Рис. 48.

Подготовлено кафедрой информационных систем и технологий ИОИТ.

 ООО УГТУ-УПИ, 2010

Терминология и задачи распознавания образов

Квазар

Пакет КВАЗАР является самостоятельным програм­мным средством, предназначенным в основном для реше­ния задач распознавания образов:

1. задачи классификации на основе обучения по прецедентам;

2. задачи таксономии;

3) задачи выбора информативной подсистемы при­знаков из заданной системы описания объектов.

Кроме того, с помощью пакета можно решать задачи:

• формирования обучающей и проверочной выборок с целью последующего использования их при решении задачи обучения по прецедентам.

Стандартная модель входных данных РО

Как известно, методы распознавания образов и многомерной статистики обычно работают с множествами объектов (ситуаций, явлений, процессов), информация о которых задается в виде значений некоторого фикси­рованного набора признаков. Таким образом, исход­ными данными для пакета является множество век­торов

Здесь — число векторов, — число признаков, — вектор ( -е наблюдение). Или, иначе говоря, на вход пакета подается матрица типа «объект-признак» следую­щего вида:

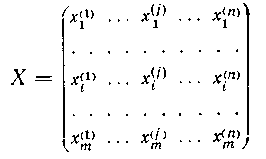
Здесь -я строка представляет собой -е наблюдение, а -й столбец образован значениями, которые прини­мает -й признак в различных наблюдениях.

В основном пакет КВАЗАР работает с данными в виде векторов, координатами которых могут быть про­извольные вещественные и lдвоичные числа.

Как правило, данные первого типа перед обработкой подвергаются преобразованию, которое заключается в нормировании значений признаков по следующему пра­вилу:

где — минимальное значение -го признака, — разность между максимальным и минимальным значе­ниями -го признака, — величина, выражающая значения -го признака -го вектора до и после норми­рования, — знак присваивания значения.

Нормирование позволяет избавиться от априорной неравнозначности признаков, обусловленной наличием у каждого признака своего интервала принимаемых им значений.

Задача классификации на основе обучения по прецедентам. Задача обучения с учителем

Пусть известны классов объектов , которые в заданном множестве представлены конечными подмножествами векторов, моделирующих соответствующие объекты из указанных классов; при этом .

Необходимо найти правило, с помощью которого можно было бы достаточно надежно классифицировать объекты (векторы) из клас­сов .

Критерием качества искомого решаю­щего правила часто служит процент правильно распо­знанных с его помощью векторов проверочной выборки. В пакете КВАЗАР проверочная выборка представляет собой часть векторов множества X, не участвующих в обучении.

Рис. 1.1. Пример линейного разделения двух множеств на плоскости

На рис. 1.1 представлен пример построения линей­ной разделяющей функции в для случая двух классов ( и ). Однако задача дискриминантного анализа не так проста, как это может показаться. Основные трудности при решении большинства практических задач состоят в том, что приходится иметь дело с мно­жествами векторов, размерность которых значительно больше двух. Кроме того, обучающие множества обычно не являются линейно разделимыми, и поэтому, как правило, приходится применять методы построения разделяющих поверхностей сложной формы.

Уточним здесь, какой смысл при работе с пакетом КВАЗАР вкладывается в понятие «решающее правило». Решающее правило можно определить как некоторым образом организованную совокупность числовых дан­ных, получаемую обычно в процессе обучения и срав­нительно несложную последовательность операций, при­водящих к классификации предъявленного вектора на основе использования этой совокупности данных.

На­пример, в случае линейного разделения двух множеств в это может быть вектор коэффициентов разделяю­щей гиперплоскости и алгоритм, который сначала вы­числяет скалярное произведение данного вектора с распознаваемым, а затем анализирует знак получен­ного скалярного произведения и выдает результат клас­сификации. Последовательность операций, приводящая к классификации вектора, обусловливает класс распознающих алгоритмов, а совокупность числовых данных определяет конкретный алгоритм распознавания. Учи­тывая это и полагая последовательность операций, используемых при классификации, в рамках того или иного метода (подхода) некоторой постоянной состав­ляющей, будем в дальнейшем под решающим правилом упрощенно понимать только соответствующую совокуп­ность числовых данных. Часто, как отмечалось, эти данные представляют собой результат решения задачи обучения и описывают границу, разделяющую классы. Однако в рамках некоторых подходов классификация может производиться без предварительного построения разделяющих границ в явном виде. В качестве решаю­щего правила, т. е. совокупности числовых данных, определяющих конкретный распознающий алгоритм, в таких случаях используются непосредственно векторы обучающей выборки. В качестве примера здесь можно назвать задачу классификации на основе метода бли­жайших соседей.

Для решения задачи в пакете используются четыре алгоритма:

1. алгоритм классификации с использованием одно­родных комитетов большинства ;

2. алгоритм классификации с использованием коми­тетов старшинства ;

3) рекуррентный алгоритм линейного разделения выпуклых оболочек двух множеств ;

4. алгоритм классификации на основе метода потен­циальных функций.

Алгоритмы реализованы в пакете в виде отдельных программных модулей. Модули в основном однотипны и предназначены для выполнения следую­щих операций:

а) построение решающего правила (обучение);

б) оценка качества решающего правила;

в) рабочее распознавание;

г) запоминание решающего правила во внешней памяти ЭВМ.

При обращении к какому-нибудь из этих модулей в обязательном порядке выполняется только первая опе­рация — построение решающего правила, необходимость выполнения остальных операций определяется конкретным заданием пользователя.

В дальнейшем, говоря о каком-либо из перечислен­ных алгоритмов, будем иметь в виду соответствующий программный модуль со всеми его возможностями.

В общих чертах характеризуя реализованные в па­кете алгоритмы обучения по прецедентам, можно отме­тить следующее. Первый и третий алгоритмы пред­назначены для решения задачи при наличии двух раз­деляемых классов; другие алгоритмы могут работать с числом классов от двух до двадцати пяти.

Первый алгоритм позволяет получить несколько различных решающих правил, безошибочно классифицирующих материал обучения (при условии, что нет одинаковых векторов в обучающих выборках разных классов).

Четвертый алгоритм предназначен для линейного раз­деления классов, если такое разделение возможно. В случае пересечения выпуклых оболочек обучающих подмножеств пользователю выдается соответствующее сообщение.

Первые четыре алгоритма могут работать как с контролем качества решающего правила по про­верочной выборке, так и без такого контроля. Обучение без контроля является, конечно, вынужденным режи­мом, и применять его следует лишь в крайних случаях, при работе с очень малым числом векторов.

Интересно также отметить, что решающие правила, получаемые с помощью первого и третьего алгоритмов, позволяют не только классифицировать объект, но и дать количественную оценку степени его принадлежно­сти соответствующему классу. Делается это путем вы­числения так называемого индекса принадлежности.

Решающие правила, как уже сказано выше, могут быть использованы для классификации как непосред­ственно после их построения, так и при последующих обращениях к пакету. В пакете имеется специальный программный модуль, обеспечивающий классификацию векторов с помощью ранее полученных решающих правил