ЗМІСТ

Вступ…………………………………....……………………………...... 3

1. Теоретична частина……….....………………………………...… 5

   1. Детермінована модель.......................………………………...…... 5

2. Типи детермінованної моделі………………………………......... 7

3. Детермінований аналіз…....……………………………...…...…... 9

4. Факторний аналіз……..…………………………..……………..... 13

1.1.5 Детермінованний факторний аналіз…………………...………..... 13

1.2 Стохастична модель..............................…………………………….. 14

1.2.1 Передумови які необхідні для створення стохастичної моделі 15

1.2.2 Етапи будування стохастичної моделі........................................ 18

1.2.3 Стохастичній аналіз..........................……………………..……… 20

1.2.4 Методи стохастичного факторного аналізу……………………. 21

2. Розрахункова частина........................................………………....... 24

2.1 Приклад розрахунку детермінованної моделі……...…………… 24

2.2 Приклад розрахунку стохастичної моделі......…………………... 28

Висновки………………………………………………………………… 34

Літератіра……………………………………………………………….. 35

Ходак Х.О.

ОНПУ ИПТДМ МЛ-101

Вступ

Мета роботи: вивчити детерміновану і стохастичну модель, описати способи їх вирішення, визначити недоліки і переваги цих моделей. провести розрахунки за допомогою математичної моделі.

Наука моделювання полягає в розділенні процесу моделювання (системи моделі на етапи підсистеми, підмоделі) детального вивчення кожного етапу взаємних зв’язків, стосунків між ними і потім опису з максимальною мірою формалізації і адеквації. Моделювання (метод і модельний експеримент) розглядається як особлива форма експерименту.

Моделювання –один з прийомів вивчення явищ і процесів, за допомогою якого можна чітко уявити досліджуваний об'єкт, описати його внутрішню структуру та охарактеризувати зовнішні зв'язки, дослідити і визначити вплив факторів на результативний показник. Сутність цього способу полягає в тому, що створюється модель взаємозв'язку аналізованого показника з факторними показниками, тобто відбувається конструювання моделі досліджуваного об'єкта на основі його попереднього вивчення, виділення головних, суттєвих характеристик

Існують такі види моделювання:

• Інформаційне моделювання

• Комп’ютерне моделювання

• Математичне моделювання

• Математико-картографічне моделювання

• Молекулярне моделювання

• Цифрове моделювання

• Логічне моделювання

• Педагогічний моделювання

• Статистичне моделювання

• Структурне моделювання

• Фізичне моделювання

• І т. п.

Всяке проектування починається з побудові моделі.

Модель – це будь-яке зображення, опис, схема, креслення якого-небудь об’єкта, процеса або явища, що є оригіналом моделі, які використовуються як представник останнього.

У цій роботі ми будемо розглядати детерміновану, стахостичну модель.

Якщо модель базується на загальних законах, вона називається детермінованою. Стахостична модель має особливо важливе значення при дослідженні і проектуванні великих систем зі складними зв’язками і властивостями, які важко врахувати.

1.Теоретична частина

1.1 Детермінована модель

Детермінована модель – це аналітичне представлення закономірностей, операцій и т. п., при яких для даної сукупності вхідних значень на виході системи можна отримати тільки один результат. Така модель може відображати як імовірнісну систему, так і детерміновану систему.

Для детермінованої моделі усі необхідні данні точно відомі. Таким чином, в них передбачається, що при аналізі моделі буде доступна уся інформація, яка необхідна для прийняття рішення. Приміром для детермінованої моделі може бути призначення екіпажу на кожен із щоденних авіарейсів у наступному місяці за умови, що відомо розклад рейсів, штат співробітників, законодавче обмеження на кількість робочих годин, правила роботи, встановленні профсоюзами и т. п., такі моделі дозволяють обробляти складні ситуації, в яких існують багато рішень і обмежень. Детерміновані моделі особливо корисні, коли в моделі мало невизначених неконтрольованих входів. Тому вони часто використовуються для прийняття внутрішніх по відношенню до організації рішень,як у прикладі з призначенням екіпажу літака.

Детермінована модель важлива з наступних причин:

1. Безліч різноманітних важливих управлінських проблем можна формалізувати у виді детермінованої моделей.

2. В детермінованих моделях легко накладати обмеження на змінні моделі.

3. Існують програми, які дозволяють оптимізувати детерміновані моделі с обмеженнями, тобто знаходити оптимальні рішення; навіть для моделей великої розмірності це робиться швидко и надійно.

4. Умовна оптимізація – дуже хороший спосіб упорядкованого представлення ситуації навіть у тому випадку, коли ви не збираєтесь будувати модель і оптимізувати Ії.

5. Практична робота з детермінованими моделями дозволяє

удосконалювати загальні навички створення моделей.

Детерінована модель використовуеться:

• При побудові апаратів автоматичної оптимізації режимів буріння.

•Для регулювання і оптимізації газодинамічних процесів розробки родовищ.

•При проектуванні технологічних процесів промивки та кріплення нафтових і газових свердловин.

•Для вибору оптимальної кількості матеріалу і обладнання, а також варіантів режима-технологічних параметрів при проектуванні промивки і кріплення свердловин.

•Розробка нафтових і газових родовищ.

•В екосистемах.

Розглянемо переваги та недоліки детермінованої моделі.

Недоліки:

•Низька адекватність реальній дійсності.

•Не враховується вплив одночасно двох чинників(наприклад: при аналізі відхилення обьема виробництво продукції по факторам використання засобів праці, предметів праці та живої праці призводить до повторного відображенню одних і тих же закономірностей).

•Не враховуються взаємозамінність.

Переваги:

•Простота використання.

•Можна формалізувати ряд управлінських проблем.

•Легко накладати обмеження на змінні моделі.

•Існують програми щоб ​​знаходити оптимальні рішення.

1.1.1 Типи детермінованої моделі

Розрізняють чотири типи детермінованих моделей:

1. Адитивні моделі

2. Мультиплікативні моделі

3. Кратні моделі

4. Змішані моделі являють собою комбінацію перерахованих вище моделей.

• Адитивні моделі

Адитивні моделі являють собою алгебраїчну суму показників і мають наступну математичну інтерпретацію:

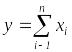(1.2.1)

В якості прикладу можна навести балансову модель товарного забезпечення:

(1.2.2)

де N_p – загальний обсяг реалізації;

N_зап.1 – запаси товару на початок періоду;

N_n – обсяг надходження;

N_выб – інше вибуття товарів;

N_зап.2 – запаси товарів на кінець аналізованого періоду.

• Мультиплікативна модель

Мультиплікативна модель являє собою твір факторів.

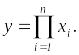(1.2.3)

Прикладом мультиплікативної моделі є двофакторна модель обсягу реалізації:

(1.2.4)

Де Ч - середньооблікова чисельність працівників;

В - виробіток на одного працівника.

• Кратні моделі

Кратні моделі являють собою відношення факторів і мають вигляд:

(1.2.5)

Де Z – сукупність показників;

(1.2.6)

Де - термін оборотності товарів (у днях);

- Середній запас товарів;

- одноденний обсяг реалізації.

• Змішані моделі

Змішані моделі являють собою комбінацію перерахованих моделей. Прикладом змішаної моделі є формула розрахунку інтегрального показника рентабельності

(1.2.7)

Де - рентабельність капіталу;

- рентабельність продажів;

- фондомісткість основних засобів;

- коефіцієнт закріплення оборотних засобів.