7.3. Синтез системы подчиненного регулирования.
Синтез системы подчиненного регулирования заключается в последовательной оптимизации соподчиненных замкнутых контуров регулирования, начиная с первого внутреннего и кончая основным внешним. При синтезе системы по заданной структуре и параметрам подобъектов регулирования определяется структура и параметры соответствующих регуляторов.
Под оптимизацией контура регулирования понимается придание контуру таких статических и динамических свойств при которых он удовлетворяет требованиям, определяются принятым критериям оптимальности. При этом необходимо отметить, что оптимизация всех соподчиненных контуров в многоконтурной системе осуществляется по единой методике и выполняется последовательно начиная с первого внутреннего конура и кончая основным внешним контуром.
Рассмотрим методику синтеза на примере одного контура подчиненного регулирования с учетом определенного критерия оптимальности. Структурная схема контура подчиненного регулирования приведены на рис. 7.3а, в которой объект регулирования представлен звеном с малой некомпенсируемой постоянной и единичным передаточным коэффициентом
(7.27)
и объектом компенсации
.
(7.28)
При этом имеется ввиду, что обратная связь в контуре не единичная.
Для определения передаточной функции регулятора по выше изложенной методике исходную структурную схему необходимо представить в виде разомкнутой структурной схемы с выходом по сигналу обратной связи, как это показано на рис. 7.3б.
Исходя из структурной схемы, некомпенсируемая постоянная времени равна
,
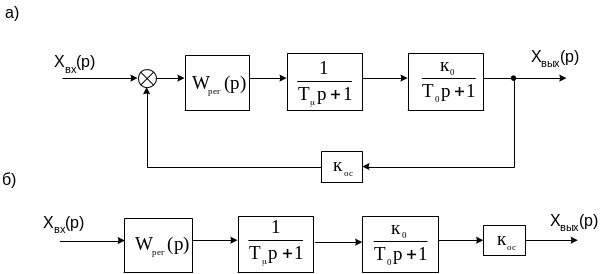
Рис. 7.3. Структурные схемы контура регулирования: а – замкнутого; б - разомкнутого.
а передаточная функция расчетного объекта компенсации запишется в следующем виде:
.
(7.29)
Подставив эти данные в ( ) получим передаточную функцию регулятора в следующем виде
.
(7.30)
Полученное выражение позволяет определить структуру регулятора, а для определения параметров регулятора необходимо знать значение коэффициента демпфирования а.
Передаточная функция замкнутого контура, учитывая (7.30), с выходом по сигналу обратной связи запишется в следующем виде
(7.31)
Из этого следует,
что динамические свойства контура, при
заданном значении некомпенсируемой
постоянной времени
,
зависят только от коэффициентов
демпфирования. Он может быть определен
из условия обеспечения оптимального
переходного процесса.
В системах подчиненного регулирования за оптимальный принимается переходный процесс в идеальном фильтре, при котором достигается максимальное быстродействие, т.е. минимальное время регулирования, при перерегулировании не превышающем 20%. Такой оптимум динамического процесса называется техническим или модульным.
Применительно к этому оптимуму желаемая передаточная функция системы второго порядка исходя из нормированной равна
.
(7.32)
Тогда, из условия
,
(7.33)
получим следующие равенства
а
;
(7.34)
а
,
(7.35)
из которых следует, что
а=1,42
2
(7.36)
Таким образом, из условия принятого оптимума динамического процесса, получено конкретное значение коэффициента демпфирования контура регулирования, в соответствии с которым определяются параметры регулятора.
Далее необходимо отметить, что при оптимизации какого-либо внешнего контура по отношению к одному или ряду внутренних контуров, в полиноме знаменателя передаточной функции не учитываются члены высшего порядка от р, а учитывается лишь член первого порядка, т.е. передаточная функция внутренних контуров равна
,
(7.37)
где с – целое число, зависящее от количества внутренних контуров