23.Сызықты дифференциалдық теңдеулер жүйесі

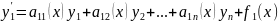
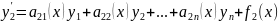(1)

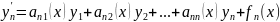
қалыпты түрде жазылған сызықты дифференциалдық теңдеулер жүйесі

деп аталады.Мұнда х a≤x≤b [a,b] сегментінде өзгереді.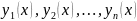

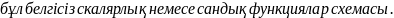Егер бұл функциялар сипаттамасы I жүйенің әрбір теңдеуін тепе теңдігіне айналдырса онда,бұл функциялар схемасы онда бұл I жүйенің шешімі деп аталады.

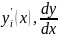i=1,2,…,n.

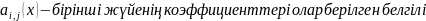
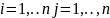функциялардың коэффициенттері және [a,b]сегментінде үзіліссіз.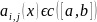

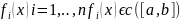жүйенің (1) түрдегі жазылып,кейде координаталық түрде жазылуы дейді.

Теорема:(Сызықты жүйе үшін)Егер (1) сызықты жүйенің коэффициенттері немесе бос мүшелері а,в үзіліссіз болса,онда (1)жүйенің алғашқы шарттарды қанағаттандыратын а,в сегментінде анықталған жалғыз шешімі бар болады.

Сызықты жүйенің вектор матрицалық жазылуы

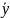(x)=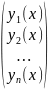 ≡colon[ ]

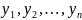(x)=

24.Іргелі матрица.

Коэффициенттері тұрақты біртекті сызықты жүйені қарастырайық. 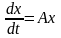(1)

Мұнда 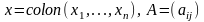- тұрақты нақты квадрат матрица.

Мұнда 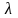-белгісіз сан, -нөлдік емес белгісіз тұрақты вектор.

Осы 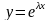өрнекті (1) жүйеге қойсақ,

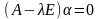
түріндегі векторлық алгебралық теңдеу аламыз. Бұл теңдеуді ашып жазсақ,

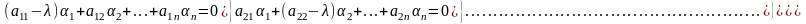
сызықты теңдеулер жүйесін аламыз. Жүйенің нөлдік емес шешімі бар болуы үшін оның анықтауышы нөлге тең болуы керек:

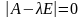немесе

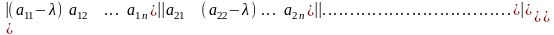
Осы теңдеу берілген жүйенің сипаттаушы теңдеуі деп аталады

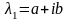- сипаттаушы теңдеудің жәй түбірі болсын. Онда оның түйіндесі 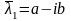саны да сол теңдеудің түбірі болады. Бұл жағдайда сәйкес шешім

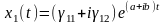
түрінде жазылады. Соңғы қатынастың нақты және жорамал бөліктерін ажыратайық:

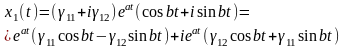
Жүйенің коэффициенттері нақты болғандықтан, комплекс шешімнің нақты және жорамал бөліктері өз алдарына нақты шешімдер болып табылады. Сондықтан,

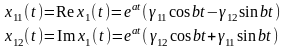
функциялары берілген жүйенің нақты шешімдері болады. Бұл шешімдер өзара сызықты тәуелсіз.Түйіндес 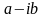түбірі жаңа тәуелсіз шешімдер тудырмайды. Демек, бір жұп комплексті түбірге өзара тәуелсіз екі нақты шешім сәйкес келеді. Олар өзара сызықты тәуелсіз болғандықтан, фундаменталь шешімдер жүйесіне кіреді. Осы сияқты, барлық түбірлер үшін нақты шешімдерді құрып шығуға болады. Олардың сызықты комбинациясы жүйенің жалпы шешімін береді.

25. Вронский анықтауышы.

Алдымен біртекті теңдеуді қарастырайық:

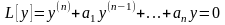(1)

Мұндағы, - тұрақты нақты сандар.

Бұл теңдеудің шешімін Эйлер ұсынған әдіс бойынша

(2)

түрінде іздейміз. Мұндағы, - белгісіз тұрақты сан. Осы өрнекті (1) теңдеудің сол жағына қойсақ,

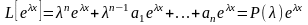(3)

қатынасын аламыз. Мұнда

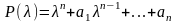(4)

(3) қатынастан 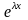функциясы теңдеудің шешімі болу үшін санының 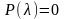теңдеуінің шешімі болуы керек екенін көреміз, яғни

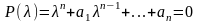(5)

Соңғы теңдеуді сипаттаушы теңдеу деп, ал оның түбірлерін сипаттаушы сандар деп атайды.

Сипаттаушы сандардың түрлеріне байланысты фундаменталь шешімдер жүйесі әртүрлі болады. Сол жағдайларды қарастырайық.

Сипаттаушы 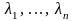сандары әртүрлі нақты сандар болсын.

Бұл сандарды кезекпен (2) қатынасқа қойып, дербес шешім табамыз:

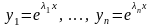(6)

Олардың сызықты тәуелсіздігін көрсету үшін Вронский анықтауышын құрайық:

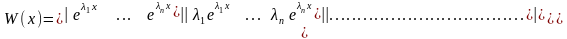
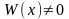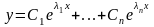Соңғы анықтауыш Вандермонд анықтауышы деп аталады. Ол сандары әртүрлі болғанда нөлге айналмайды, яғни . Сондықтан, (6) функциялар жиыны берілген теңдеудің фундаменталь шешімдер жүйесін құрайы. Бұл жағдайда жалпы шешім (7)

түрінде жазылады. Мұндағы, 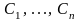- еркін тұрақты сандар.