
- •15. Жоғары ретті сызықты дифференциалдық теңдеулердің жалпы теориясы.
- •20. Сызықты дифференциалдық теңдеулер үшін Остроградский-Лиувилль формуласы
- •23.Сызықты дифференциалдық теңдеулер жүйесі
- •24.Іргелі матрица.
- •25. Вронский анықтауышы.
- •26. Жалпы шешім
- •27 Сызықты жүйенің шешімдерінің құрылымы.
- •28 Сызықты дифференциалдық жүйе үшін Остроградский-Лиувилль ф.
- •29. Сызықты дифференциалдық жүйе үшін тұрақтыларды вариациялайтын Лагранж әдісі
- •30. Ляпунов бойынша орнықтылық ұғымы.
- •31. Асимптотикалық орнықтылық. Бірінші жуықтау бойынша Ляпунов теоремасы
Дифф-дық теңдеулердің негізгі ұғымдары. Туынды бойынша шешілген бірінші ретті дифференциалдық теңдеулер. Геометриялық сипаттамасы. Коши есебі.

2)Айнымалылары ажыратылатын теңдеулер

3) Біртекті дифференциалдық теңдеулер және оларға келтірілетін теңдеулер
y’=
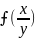 теңдеуі біртекті теңдеу деп аталады
теңдеуі біртекті теңдеу деп аталады
y’=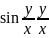 =z(x)
=> (z-x-ке тәуелді функция)
=z(x)
=> (z-x-ке тәуелді функция)
Ауыстыру арқылы интегралданады
y=xz1y’=z+z’x
z+xz’=⨍(z)
=> x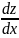 =⨍(z)-z
=⨍(z)-z
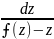 =
=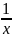 dx
(айнымалылары ажыратылатын
теңдеу)
dx
(айнымалылары ажыратылатын
теңдеу)
Біртекті теңдеуде жоғарыдағыдай ауыстыру қолдануға болады
y’=sin(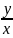 )
)
z+xz’=sin(z)
x =sin(z)-z
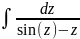 =
=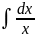 +C
+C
y’=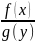 – айнымалылары ажыратылатын
теңдеу/
– айнымалылары ажыратылатын
теңдеу/
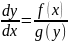 f(x)dx=g(y)dy
f(x)dx=g(y)dy
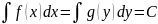
y’=f(ax+by)
z=ax+by
z’=a+by’
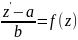
Мына түрдегі теңдеулер
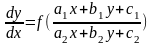 (1)
(1)
біртекті теңдеуге келтірілетін
теңдеулер деп есептелінеді. Мұнда
алдымен c1
және c2
сандарынан құтылуға
болады. Ол үшін екі түзудің
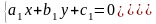
қиылысу нүктелерін тауып,
координат жүйесінің бас нүктесін сол
нүктеге көшіру керек. Айталық,
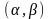 осы екі түзудің қиылысу нүктесі болсын.
Бұл жағдайда
осы екі түзудің қиылысу нүктесі болсын.
Бұл жағдайда
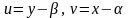
алмастыруларын енгізсек, онда берілген теңдеу біртекті теңдеуге келеді:
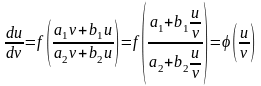 (2)
(2)
Бұл теңдеу алдындағы теңдеу
сияқты,
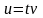 алмастыруы арқылы оңай интегралданады.
алмастыруы арқылы оңай интегралданады.
Егер жоғарыда көрсетілген
екі түзу қиылыспаса, онда
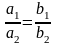 қатынасы орындалады да, бұл жағдайда
қатынасы орындалады да, бұл жағдайда
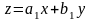 алмастыруы арқылы теңдеудің айнымалылары
оңай бөлінеді.
алмастыруы арқылы теңдеудің айнымалылары
оңай бөлінеді.
4)Бірінші ретті сызықтық теңдеулер

5)Бірінші ретті сызықтық дифф-дық теңдеу үшін еркін тұрақтыны варияциалау әдісі.

6)Бернулли теңдеуі.

7)Толық дифференциалдық теңдеу. Қажетті және жеткілікті шарт.

8) Интегралдаушы көбейткіш

9) Туынды бойынша шешілген бірінші ретті дифференциалдық теңдеу үшін Коши есебінің шешімі бар болуы және жалғыздығы туралы теорема

10) Туындысы бойынша шешілмеген дифференциалдық теңдеулер.

11) Параметр енгізу әдісі. Лагранж теңдеуі

12) Клеро теңдеуі

13) Реті төмендетілетін жоғары ретті дифференциалдық теңдеулер.
Жоғарғы ретті дифференциалдық теңдеулерді айқындалмаған
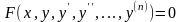 (1)
(1)
теңдеу түрінде, немесе, жоғарғы туындысы бойынша шешілген
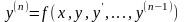 (2)
(2)
теңдеу түрінде жазуға болатыны айтылған.
Енді осы теңдеулердің ретін қандай жағдайларда төмендетіп, интегралдауды оңайлатуға болатынын көрсетейік.
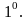 Тәуелсіз айнымалы айқын түрде
кірмеген теңдеу:
Тәуелсіз айнымалы айқын түрде
кірмеген теңдеу: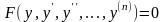 (3)
(3)
жалпы интегралы
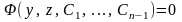 н/е
н/е
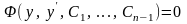 түрінде болады.
түрінде болады.
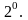 Белгісіз функция мен оның
алғашқы туындылары кірмейтін теңдеу:
Белгісіз функция мен оның
алғашқы туындылары кірмейтін теңдеу:
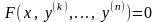 (4)
жалпы интегралы
(4)
жалпы интегралы
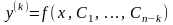 (5)
(5)
теңдеуді интегралдау арқылы табылады.
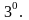 Белгісіз функция мен оның
туындылары бойынша біртекті теңдеу.
Белгісіз функция мен оның
туындылары бойынша біртекті теңдеу.
Егер (1) теңдеудегі
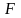 функциясы үшін
функциясы үшін
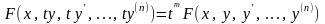
шарты орындалса, онда ол
функция
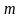 дәрежелі біртекті функция деп аталынады
да, сәйкес теңдеу функция мен оның
туындылары бойынша біртекті деп
аталынады. Бұл жағдайда
дәрежелі біртекті функция деп аталынады
да, сәйкес теңдеу функция мен оның
туындылары бойынша біртекті деп
аталынады. Бұл жағдайда
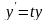 алмастыруы арқылы теңдеудің реті бір
ретке төмендетіледі. Шынында да,
алмастыруы арқылы теңдеудің реті бір
ретке төмендетіледі. Шынында да,
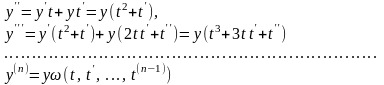
Бұл өрнектерді (1) теңдеуге
қойсақ,
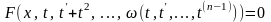
түріндегі
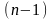 -ретті
теңдеу аламыз. Егер бұл теңдеудің
-ретті
теңдеу аламыз. Егер бұл теңдеудің
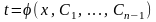
түріндегі жалпы шешімін таба алсақ, онда берілген теңдеудің жалпы шешімі
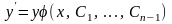 теңдеуін
интегралдаудан алынады.
теңдеуін
интегралдаудан алынады.
 Теңдеудің сол жағы басқа бір
функцияның туындысы болса, онда теңдеудің
реті бір ретке төмендейді. Шынында да,
Теңдеудің сол жағы басқа бір
функцияның туындысы болса, онда теңдеудің
реті бір ретке төмендейді. Шынында да,
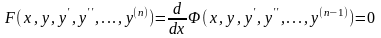
болғандықтан, бір аралық интеграл белгілі:
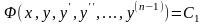 ,яғни
бастапқы теңдеудің реті бір өлшемге
кеміді.
,яғни
бастапқы теңдеудің реті бір өлшемге
кеміді.
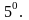 Жалпыланған біртекті теңдеу,
яғни
функциясы үшін
Жалпыланған біртекті теңдеу,
яғни
функциясы үшін
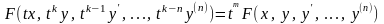
шарты орындалатын теңдеу.
Бұл жағдайда
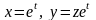 алмастыруы арқылы теңдеудің ретін бірге
кемітуге болады.
алмастыруы арқылы теңдеудің ретін бірге
кемітуге болады.
14) Толық емес теңдеулер.

Егер
(1)-теңдігі үшін
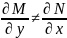 болса, онда (1)-теңдеу
толық емес дифференциал
теңдеу деп аталады.
болса, онда (1)-теңдеу
толық емес дифференциал
теңдеу деп аталады.
15. Жоғары ретті сызықты дифференциалдық теңдеулердің жалпы теориясы.
Жоғарғы ретті жәй дифференциалдық теңдеудің туынды бойынша шешілмеген түрі былай жазылады: (1)
Мұндағы,
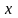 -тәуелсіз
айнымалы,
-тәуелсіз
айнымалы,
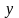 -белгісіз
функция, ал
-белгісіз
функция, ал
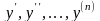 -
белгісіз функцияның туындылары
-
белгісіз функцияның туындылары
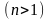 .
- кейбір
.
- кейбір
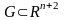 облысында анықталған нақты үздіксіз
функция. Егер (1) қатынас жоғарғы
облысында анықталған нақты үздіксіз
функция. Егер (1) қатынас жоғарғы
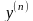 туындысы бойынша шешілсе, онда былай
жазамыз:
(2)
туындысы бойынша шешілсе, онда былай
жазамыз:
(2)
Мұндағы,
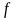 - функциясы кейбір
- функциясы кейбір
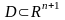 облысында анықталған үздіксіз функция
деп есептелінеді. Бұл теңдеулердің
шешімдері де бірінші ретті теңдеулердің
шешімдеріне ұқсас түрде анықталады.
облысында анықталған үздіксіз функция
деп есептелінеді. Бұл теңдеулердің
шешімдері де бірінші ретті теңдеулердің
шешімдеріне ұқсас түрде анықталады.
Анықтама-1.
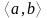 аралығында анықталған
аралығында анықталған
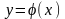 функциясы (2) теңдеудің осы аралықтағы
шешімі деп аталынады, егер ол төмендегідей
үш шартты қанағаттандырса:
функциясы (2) теңдеудің осы аралықтағы
шешімі деп аталынады, егер ол төмендегідей
үш шартты қанағаттандырса:
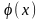 функциясы
аралығында
функциясы
аралығында
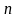 рет
рет
дифференциалданатын болса;
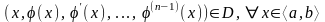 ;
;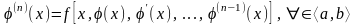 .
.
Айқындалмаған (1) теңдеудің де шешімін осы түрде анықтауға болады.
Анықтама-2. аралығында анықталған функциясы (1) теңдеудің осы аралықтағы шешімі деп аталынады, егер ол төмендегідей үш шартты қанағаттандырса:
функциясы аралығында рет
дифференциалданатын болса;
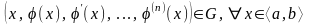 ;
;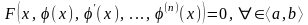 .
.
16. Біртекті дифференциалдық
теңдеулер Белгісіз
функция мен оның туындысы сызықты
түрде, яғни бірінші дәрежеде байланысқан
теңдеуді сызықты дифференциалдық теңдеу
деп атайды. Сызықты теңдеудің келтірілген
түрін қарастырайық:
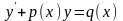 (1)
(1)
Мұнда p(x), q(x)
функциялары кейбір <a,b>
аралығында анықталған және үздіксіз
деп есептелінеді. Егер q(x)0
болса, онда (1) теңдеуді біртексіз сызықты
теңдеу деп, ал q(x)=0
болса, онда біртекті сызықты теңдеу деп
атайды:
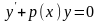 (2)
(2)
Көбінесе (2) теңдеуді (1) теңдеудің сәйкес біртектісі деп атайды.
Біртекті (2) теңдеу айнымалылары
ажыратылатын теңдеу. Екі жағын
у-ке бөліп, мынандай
теңдеу аламыз:
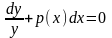
Осы қатынасты интегралдасақ:
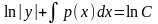 өрнегін
аламыз. Логарифмсіз жазсақ,
өрнегін
аламыз. Логарифмсіз жазсақ,
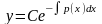 (3)
(3)
түріндегі (2) теңдеудің жалпы шешімін аламыз. Егер y=0 жағдайды қарастырсақ, ол осы жалпы шешімнің С=0 болғандағы мәніне сәйкес келетін шешім. Сондықтан y=0 – дербес шешім. Оны нөлдік немесе тривиaл шешім деп те атайды және ол барлық уақытта бар шешім.
Біртекті (2) теңдеудің (3) жалпы шешімін Коши түрінде жазсақ, былай жазылады:
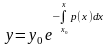 (4)
(4)
мұнда х0 -тұрақты сан, ал у0 – кез келген сан деп есептелінеді.
Біртекті теңдеу шешімдерінің екі қасиетін атап өтейік:
10. Егер у1 және у2 функциялары (2) теңдеудің шешімдері болса, онда олардың қосындысы: уу1+у2 функциясы да сол теңдеудің шешімі болады.
20.
Егер у1
функциясы (2) теңдеудің шешімі болса,
онда
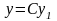 функциясы да (С –
кез келген сан) сол теңдеудің шешімі
болады.
функциясы да (С –
кез келген сан) сол теңдеудің шешімі
болады.
17. Фундаменталь шешімдер
жүйесі және оның табылуы.
Біртексіз жүйенің жалпы және дербес
шешімін іздегенде
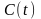 векторын координаттары бойынша іздеген
қолайлы. Олардың туындылары сызықты
алгебралық жүйенің шешімдері ретінде
анықталады. Айталық,
векторын координаттары бойынша іздеген
қолайлы. Олардың туындылары сызықты
алгебралық жүйенің шешімдері ретінде
анықталады. Айталық,
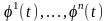 вектор - функциялары
вектор - функциялары
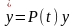 (1) жүйенің фундаменталь
шешімдер жүйесі болсын. Онда осы жүйенің
жалпы шешімі
(1) жүйенің фундаменталь
шешімдер жүйесі болсын. Онда осы жүйенің
жалпы шешімі
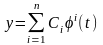 түрінде
жазылады. Мұндағы,
түрінде
жазылады. Мұндағы,
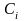 - еркін тұрақтылар.Енді
- еркін тұрақтылар.Енді
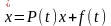 жүйенің
жалпы шешімін табу үшін осы
- лерді
жүйенің
жалпы шешімін табу үшін осы
- лерді
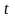 -
ға байланысты үздіксіз дифференциалданатын
белгісіз функциялар деп есептейік, яғни
-
ға байланысты үздіксіз дифференциалданатын
белгісіз функциялар деп есептейік, яғни
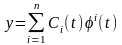 (2)
(2)
Егер осы вектор-функцияны
(1) жүйеге қойсақ, белгісіз
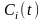 және оның туындысы
және оның туындысы
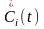 бойынша төмендегідей векторлық теңдеу
алынады:
бойынша төмендегідей векторлық теңдеу
алынады:
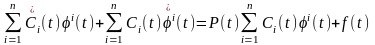
Осыдан,
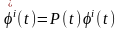 екенін ескерсек,
екенін ескерсек,
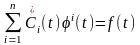 (3) түріндегі векторлық теңдеу аламыз.
Оны координаттары бойынша ашып жазсақ,
төмендегідей
скалярлық теңдеулер жүйесін аламыз:
(3) түріндегі векторлық теңдеу аламыз.
Оны координаттары бойынша ашып жазсақ,
төмендегідей
скалярлық теңдеулер жүйесін аламыз:
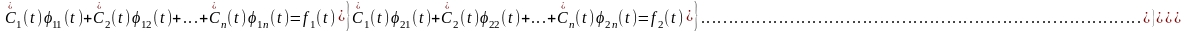 (4)
(4)
Бұл жүйе алгебралық сызықты біртексіз жүйе. Ал оның негізгі анықтауышы Вронский анықтауышы болғандықтан, ол нөлге тең емес. Крамер ережесі бойынша барлық функциялары бір мәнді болып анықталады:
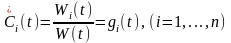 (5)
(5)
Осыдан
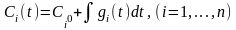 (6)
(6)
Бұл функцияларды (17) қатынасқа қойсақ,
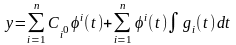 (7)
(7)
түріндегі (1) жүйенің жалпы шешімін аламыз. Мұндағы, бірінші қосынды біртекті жүйенің жалпы шешімін береді де, екінші қосынды (1) жүйенің дербес шешімін береді. Сонымен, бастапқы тұжырымға қайта келдік: біртексіз сызықты жүйенің жалпы шешімі сәйкес біртекті жүйенің жалпы шешімі мен біртексіз жүйенің дербес шешімінің қосындысынан тұрады.
18.Вронскиан
Айталық,
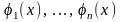 функциялары (1) теңдеудің
аралығында анықталған нақты шешімдері
болсын. Осы функциялар мен олардың
туындыларынан құрылған төмендегідей
ретті анықтауыш
функциялары (1) теңдеудің
аралығында анықталған нақты шешімдері
болсын. Осы функциялар мен олардың
туындыларынан құрылған төмендегідей
ретті анықтауыш
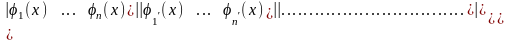 (5)
(5)
Вронский анықтауышы деп
аталады. Қысқаша, оны функциялардың
вронскианы дейді. Бұл анықтауышты
қысқаша,
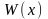 деп белгілейді.
деп белгілейді.
Теорема-3. Егер шешімдері аралығында сызықты тәуелді болса, онда олардың вронскианы осы аралықта нөлге тепе-тең.
Дәлелдеуі.
Анықтама бойынша бәрі бірдей нөлге тең
емес
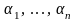 сандары үшін
сандары үшін
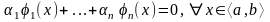 (6)
(6)
теңдігі орындалады.
Осы қатынасты
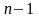 рет дифференциалдау арқылы сызықты
алгебралық жүйе құрайық:
рет дифференциалдау арқылы сызықты
алгебралық жүйе құрайық:
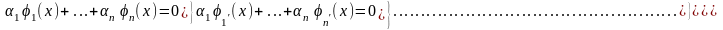 (7)
(7)
Бұл біртекті сызықты алгебралық
жүйенің нөлдік емес шешімі бар болуы
үшін оның анықтауышы нөлге тең болуы
керек, ал ол анықтауыш Вронский анықтауышы,
яғни
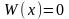 .
.
Теорема-4. Егер шешімдері аралығында сызықты тәуелсіз болса, онда олардың вронскианы осы аралықтың бірде-бір нүктесінде нөлге айналмайды.
Дәлелдеуі.
Кері жориық, кейбір
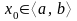 нүктесі үшін
нүктесі үшін
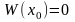 болсын. (7) жүйені бір нүкте үшін қайта
құрайық:
болсын. (7) жүйені бір нүкте үшін қайта
құрайық:
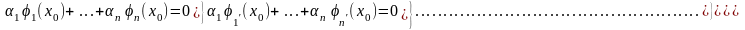
Бұл жүйенің анықтауышы болғандықтан, нөлге тең емес шешім бар:
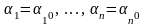
Осы сандар арқылы құрылған
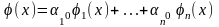
функцияны қарастырайық. Бұл
қосынды (1) теңдеудің шешімі болатыны
1-теоремада көрсетілген және ол (2)
бастапқы шарттарды қанағаттандырып
тұр. Сондықтан, шешімнің жалғыздығы
бойынша
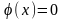 .
Демек,
.
Демек,
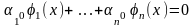
Мұндағы,
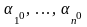 бәрі бірдей нөлге тең емес. Соңғы қатынас
функцияларының сызықты тәуелділігін
көрсетеді. Ал бұл теореманың шартына
қайшы. Сондықтан,
бірде-бір нүктеде нөлге тең болмайды.
Бұл шарт әрі жеткілікті – егер берілген
шешімдердің вронскианы нөлге тең
болмаса, онда олар берілген аралықта
сызықты тәуелсіз. Бұл тұжырымды да кері
жору арқылы оңай дәлелдеуге болады.
бәрі бірдей нөлге тең емес. Соңғы қатынас
функцияларының сызықты тәуелділігін
көрсетеді. Ал бұл теореманың шартына
қайшы. Сондықтан,
бірде-бір нүктеде нөлге тең болмайды.
Бұл шарт әрі жеткілікті – егер берілген
шешімдердің вронскианы нөлге тең
болмаса, онда олар берілген аралықта
сызықты тәуелсіз. Бұл тұжырымды да кері
жору арқылы оңай дәлелдеуге болады.
19.Біртекті теңдеудің жалпы шешімінің құрылымы.Біртекті сызықты теңдеудің шешімдерінің қасиеттерін келтірейік. Коэффициенттері кейбір аралығында үздіксіз болып келетін мына -ретті теңдеуді қарастырайық:
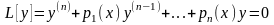 (1)
(1)
Ең алдымен ескеретін жәй – біртекті сызықты теңдеудің барлық жағдайда нольдік шешімі бар. Ол шешім
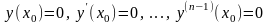 (2)
(2)
бастапқы шартты қанағаттандыратын
Коши есебінің шешімі:
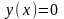 .
Бұл шешім жалғыз.
.
Бұл шешім жалғыз.
Теорема-1.
Егер
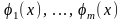 функциялары (1) теңдеудің
аралығындағы шешімдері болса, онда
олардың сызықты комбинациясы
функциялары (1) теңдеудің
аралығындағы шешімдері болса, онда
олардың сызықты комбинациясы
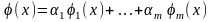 (3)
(3)
сол теңдеудің аралығындағы шешімі болады.
Дәлелдеуі.
Шарт бойынша әрбір
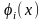 шешім:
шешім:
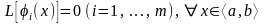
Енді сызықты дифференциалдық оператордың қасиетін пайдалансақ, онда
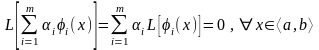
Теорема-2.
Егер (1) теңдеудің
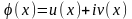 түріндегі комплекс шешімі бар болса,
онда оның нақты және жорамал бөліктері
өз алдына сол теңдеудің шешімдерін
береді.
түріндегі комплекс шешімі бар болса,
онда оның нақты және жорамал бөліктері
өз алдына сол теңдеудің шешімдерін
береді.
Дәлелдеуі. Шарт бойынша
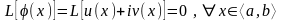
оператордың қасиеті бойынша
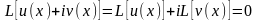
Осыдан
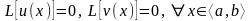 .
.
Анықтама-1. Егер аралығында анықталған
функциялары үшін бәрі бірдей
нөлге тең емес
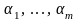 сандары табылып,
сандары табылып,
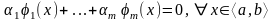 (4)
(4)
теңдігі орындалса, онда берілген функциялар жиыны аралығында сызықты тәуелді деп аталынады, ал (4) теңдік сандарының тек нөлдік мәндерінде ғана орындалса, онда берілген функциялар жиыны аралығында сызықты тәуелсіз деп аталады.
