3 Вопрос. Внутренняя энергия и энтальпия.

Внутренняя энергия U является экстенсивным свойством газа, т.е. зависит от его массы (в противоположность свойствам, не зависящим от массы и называемым интенсивными ). Поэтому для большей определенности внутреннюю энергию газа обычно относят к единице массы (1кг). Такая удельная внутренняя энергия обозначается буквой u. Таким образом, если масса рассматриваемого газа равна М кг, то

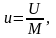Дж/кг. (1.5)

Из самого определения внутренней энергии вытекает, что каждому состоянию газа соответствует одно и только одно значение внутренней энергии. Это означает, что внутренняя энергия представляет собой однозначную функцию состояния или, иначе, однозначную функцию любых двух независимых параметров, определяющих это состояние.

Поэтому изменение внутренней энергии в каком – либо процессе не зависти от характера процесса, а однозначно определяется заданными начальным и конечным состояниями газа. Так, в процессах а,b и с (рис 1.1.), в которых начальные и конечные состояния газа одинаковы, одинаковыми будут и изменения внутренней энергии :

.

Математически это означает, что дифференциал du является полным дифференциалом функции и может быть представлен равенством

Рисунок 1.1

. (1.6)

Очевидно, что если процесс замкнут, т.е. если после завершения его газ возвращается в исходное состояние (такие процессы в термодинамике называются круговыми процессами или циклами), то изменение внутренней энергии в нем будет равно нулю:

.

Как нетрудно видеть, аналогичными свойствами обладают все рассмотренные выше параметры: p, и Т. Следовательно, и внутренняя энергия может служить параметром состояния газа. Как и все другие параметры состояния, измеряемые в тепловых единицах (Дж), она относится к калорическим параметрам, а уравнение состояния, в состав которого входит внутренняя энергия (или какой – либо другой калорический параметр), например уравнение

называется калорическим уравнением состояния.

Наряду с внутренней энергией в дальнейшем изложении основ технической термодинамики важную роль играет величина

, кДж/кг , (1.7)

называемая энтальпией газа. Будучи составленной из функций состояния, энтальпия сама является функцией состояния и играет роль одного из калорических параметров состояния. Очевидно, что все свойства функции состояния имеет и энтальпия. Например, если задана зависимость ,то

, (1.8)

т.е. дифференциал энтальпии является полным дифференциалом.

Равным образом, для цикла

,

а для незамкнутого процесса 1–2

,

независимо от пути, по которому протекает процесс.

Энтальпия представляет собой в общем случае чисто математическую величину и приобретает конкретный физический смысл лишь применительно к процессам, протекающим в газовом потоке, которые будут рассматриваться ниже.

4 Вопрос. Работа изменения объема рабочего тела.

1.5 Работа изменения объема рабочего тела

Всякое изменение объема газа сопровождается совершением работы. При расширении газ совершает работу против внешних сил, при сжатии внешние силы совершают работу над газом.

Положим, что 1 кг газа, расширяясь в цилиндре двигателя (рис. 1.2), перемещает поршень из положения А в положение В, причем процесс изменения состояния газа в – диаграмме изображается линией 1-2.

Н а элементарном отрезке пути поршня a – b, равном ds, изменением давления можно пренебречь, поэтому элементарная работа газа на этом участке составляет:

,

где F– площадь поршня и, следовательно, pF– сила, действующая на поршень.

С другой стороны, , следовательно,

, кДж/кг. (1.9)

О

Рисунок 1.2

чевидно, что суммарная работа, совершаемая газом в процессе 1–2, составит:

, кДж/кг. (1.10)

Если газ расширяется, то >0 и l > 0, т.е. работа расширения газа есть величина положительная. Если газ сжимается, то <0 и l < 0, т.е. работа сжатия газа есть величина отрицательная.

Из – диаграммы видно, что элементарная работа dl графически изображается площадью прямоугольника с основанием и высотой р (заштрихованная на графике). Следовательно, полная работа изменения объема в процессе 1–2 изображается площадью, расположенной между линией процесса и осью абсцисс и ограниченной справа и слева ординатами крайних точек процесса (т.е. площадью 1–2–3–4–1, которая и соответствует геометрически приведенному выше интегралу).

Графическая интерпретация работы в – диаграмме наглядно показывает, что ее величина зависти от того, каким путем газ переходит из начального состояния в конечное. Поэтому можно сказать, что работа является функцией процесса и при одинаковых начальных и конечных состояниях газа может быть различной в зависимости от того, по какому пути совершается этот процесс. Отсюда же вытекает, что работа l не является функцией состояния, а ее дифференциал dl не является полным дифференциалом.

Е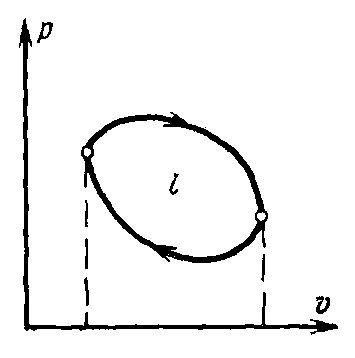

Рисунок 1.3

сли по завершении процесса в двигателе поршень возвращается в исходное положение, а газ – в исходное состояние, то в цилиндре осуществляется термодинамический цикл, изображаемый в – диаграмме замкнутой кривой (рис. 1.3). Работа газа за цикл в целом будет положительной, если линия расширения расположена выше линии сжатия (т.е., если линия цикла направлена по часовой стрелке, как показано на рисунке), ибо в этом случае положительная работа расширения по абсолютной величине меньше отрицательной работы сжатия. В первом случае цикл называется прямым, а во втором – обратным, причем в обоих случаях работа газа за цикл измеряется площадью, ограниченной линией цикла.