Экзаменационные вопросы по математике / Ответы в одном файле

1.Определитель. Определение и свойства. Понятие перестановки. Чётность перестановки. Разложение определителя по элементам строки и столбца.

Определитель (детерминант) А n-ого порядка квадратной матрицы А – называется сумма всевозможных произведений из n элементов матрицы, взятых из каждой строки и каждого столбца со знаком, определяющим выражение (-1)ti+tj, где ti – чётность перестановки из

индексов строк, а tj – чётность перестановки из индексов столбцов.

Det A = ∑(-1)ti+tjai1j1*ai2j2*ai3j3*…*ainjn.

Перестановкой из n чисел (элементов) называется упорядоченное расположение этих чисел друг за другом.

Инверсия перестановки – изменение порядка следования (большее число идёт за меньшим).

Если общее число инверсий чётное, то перестановка чётная, а если общее число инверсий нечётное – то перестановка нечётная.

Свойства перестановок.

Oвзаимное изменение положение 2х элементов перестановки называется транспозицией. abcd ->dbca

Утверждение: 1 транспозиция меняет чётность перестановки.

1)Соседние – ai1, ai2, …, aik, aij, …, ain -> ai1, ai2, …, aik, aij, …, ain

2)Несоседние - ai1, ai2, …, aik, aik+1, aik+2 ,…, aik +p, …, ain - p соседних транспозиций +p-1 = 2p-1

1 2 3 … … n

n(n+1)(n+2)…*1=n! (произведение последовательных натуральных чисел)

OТранспозиция несоседних элементов.

Утверждение: Все n! перестановок из n чисел могут быть расположены последовательно друг за другом так, что каждая последующая перестановка получится из предыдущей путём 1 транспозиции.

Доказательство (метод индукции).

1)n=2 – Утверждение верно. 1 2 2 1

2)Если предположить, что утверждение верно для числа n-1, то из этого следует его справедливость для числа n.

i1,i2,i3,…,in

-зафиксируем 1 элемент и совершим возможные перестановки n-1.

-затем зафиксируем 2 элемент. Осталось n-2 перестановок и т.д.

Из этого следует, что любые 2 перестановки могут быть получены из любой другой конечным числом транспозиций.

n! – всегда чётное число -> если расположить члены друг за другом, то количество чётных перестановок = количеству нечётных.

Вывод: в каждом определителе число отрицательных членов = числу положительных.

Свойства определителей.

Транспонирование не меняет определителя. (Транспонирование – взаимная замена строк и столбцов.)

=

Возьмём любой член определителя (-1)ti+tjai1j1*ai2j2*ai3j3*…*ainjn.

Из вида любого члена определителя видно, что при транспонировании они не меняются. det AT = det A

1)Если в определителе поменять местами 2 строки, то знак определителя поменяется на противоположный.

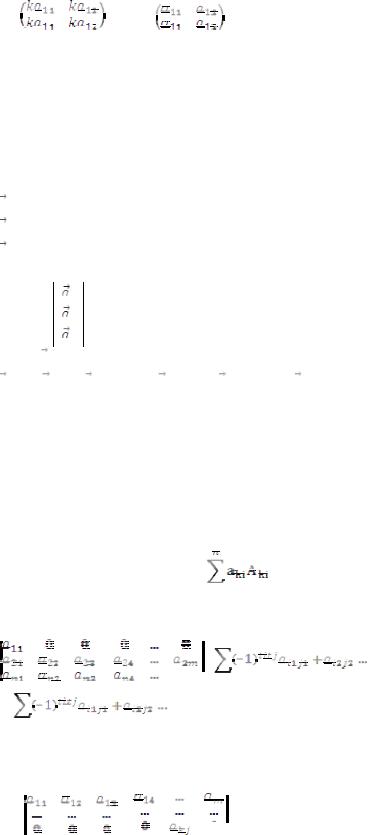
Доказательство: Берём произвольный член определителя. Взаимное расположение -> поменялись первые 2 индекса -> чётность изменилась -> изменился знак.

2)Если в определителе 2 строки (столбца) одинаковы, то det = 0.

Если 2 одинаковые строки поменять местами, то ничего не меняется, но по св-ву 2 знак меняется. Это происходит, если =0. ( =- , 2 =0, =0)

3)Если в определителе есть 2 пропорциональные строки, то он тоже = 0.

после того, как k вынесен, 2 строки равны. По св-ву 3 =0.

4)Если в некоторой строке определителя все элементы в виде 1 и той же комбинации чисел, а именно k-я строка (αck1 + βdk1 + αck2+ βdk2) = α|ck1+ck2…+ckn|+β|dk1+dk2…+dkn|.

5)Если в любой строке определителя прибавить любую другую строку с противоположным коэффициентом, то определитель не изменится.

6)Если строка в определителе состоит из нулей, то определитель = 0.

7)Если какая-либо строка определителя есть линейная комбинация других строк, то определитель

=0.

1 = (a11,a1n)

2 = (a21,a2n)

n = (an1,ann)

1

Det A=

2

n

Пусть k есть линейная комбинация остальных

k = α11 + α2 2 +…+ αk-1k-1 + αk+1 k+1 +…+ αn n

В соответствии со свойством 7 определитель равен сумме этих определителей, равных нулю. Количество определителей = (n-1)и в каждой из которых имеются одинаковые строки. Разложение определителя по элементам строки или столбца.

Минором элемента определителя aik называется определитель n-1 порядка, получающийся вычёркиванием строки и столбца, на пересечении которых стоит элемент aik. Алгебраическим дополнением Аik элемента определителя aik называется Aik = (-1)i+kMik. Теорема. Определитель равен сумме произведений элементов какой-либо строки на их алгебраические дополнения.

det A = ak1Ak1+ak2Ak2+…+aknAkn =

1) Доказательство: Пусть определитель имеет вид:

=

a11

Определитель 1 порядка, полученный вычёркиванием 1 строки и 1 столбца. Тем самым, для 1 случая теорема доказана.

2) Пусть определитель имеет вид:

= (-1)j

an1 an2 an3 an4 … anm

Передвинем последовательными шагами столбец этого элемента akj (столбец с номером j) влево до занятия им места 1 столбца. При этом определитель при каждом шаге меняет знак и итоге приобретает множитель (-1)j и приобретает вид:

Далее перемещаем строку с номером k вверх последовательно, пока она не займёт место 1ой строки, т.е. определитель будет иметь вид:

anj an1 an2 an3 … anm

При этом определитель приобретает ещё один множитель (-1)k. В итоге

anj an1 an2 an3 … anm

Мы пришли к 1 случаю, для которого справедливость была доказана. det A = (-1)j+kakjMkj+0*Ak1+…+0*Ak2 *…*0*Akn

3) Общий случай.

a11 a12 … a1m

…… … …

=(-1)k+1ak1Mk1+(-1)k+2ak2Mk2+…+(-1)k+naknMkn

Это правило вычисления определителя называется разложением по I строке (столбцу).

2. Равенство нулю суммы произведений элементов строки (столбца, алгебраическое дополнение другой строки (столбца)).

Сумма произведений элементов какой-либо строки на алгебраическое дополнение другой строки равна нулю, т.е. :

(*) аk1Аj1+ аk2Аj2+…+ аknАjn=0 Доказательство: Рассмотрим определитель:

Ввыражении (*) коэффициент Аjm получились вычёркиванием j-ой строки -> аjmА не зависят от тех чисел, которые могут стоять в j-ой строке.

Вопределителе (**) на место j-ой строки поставим k-ую строчку. Тогда этот определитель

равен det А = аk1Аj1+ аk2Аj2+…+ аknАjn

Но это равенство равно нулю, так как определитель имеет две одинаковые строки. Ч.т.д.

3.Ранг матрицы. Вычисление ранга методом окаймляющих миноров. Пусть имеется прямоугольная матрица nхm .

Минором K-ого порядка матрицы А (k<m,k<n) называется определитель, получающийся из элементов, стоящих на пересечении каких-либо строк и каких-либо столбцов.

Рангом матрицы называется целое, положительное число r=Rang А, такое, что в данной матрице присутствует хотя бы один минор порядка r≠0, а все миноры следующего порядка (r+1 и далее) =0.

Метод окаймления миноров.

Если в матрице найден отличный от нуля минор k-ого порядка, то все миноры k+1 порядка считать не обязательно, так как имеет место теорема:

Если все окаймляющие данный минор k-ого порядка миноры k+1 порядка равны нулю, то и все вообще миноры k+1 –ого порядка = 0.

Найдём окаймляющие миноры 3-его порядка для M2 : (положим, М2≠0)

4.Теорема о базисном миноре. Понятие линейно независимых строк (столбцов) определителя. Необходимое и достаточное условие равенства 0 определителя.

При нахождении ранга матрицы минор порядка r (ранг матрицы) называется базисным.

Все строки матрицы являются линейными комбинациями строк базисного минора. (к столбцам относится то же самое).

Доказательство:

Берём любую строку с номером произвольным k. Ставим её под базисный минор. Вправо от минора ставим произвольный столбец с номером j. Рассмотрим минор Mr+1, окаймляющий базисный снизу. K-ой строкой, справа k-ым столбцом.

Разложим его:

Mr+1=0=c1a1j+ c2a2j+ crarj+ Arakj |:Ar (Ar≠0) Akj=-c1*a1j/Ar- c2*a2j/Ar+…- cr*arj/Ar

Так как akj – координаты вектора строки с номером k, это вернодля любого столбца (коэффициенты ci/Ar одинаковы для любого j) -> сам вектор

строка ak=-c1a1/Ar- c2a1/Ar -crar/Ar

х1, х2, …, хn – неизвестные

aik – постоянные коэффициенты

Матрица системы:

1)Кмножаем каждую строку системы на алгебраическое дополнение 1-ого элемента строки.

2)Сложим уравнения.

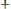
*x1 + *x2 + … +

*xn =

3)Поступим так же со вторым столбцом. (каждый элемент строки умножаем на А второго элемента строки). Слева получим х2 , справа - 2

Если определитель системы ≠0, то система имеет, и притом единственное, решение, даваемое формулами крамера:

– определитель системы, составленный из коэффициентов при неизвестных.

i – определитель, получаемый из определителя системы заменой столбца коэффициентов при неизвестном определяемом столбце свободных членов.

Если определитель системы = 0:

Если хотя бы один i ≠ 0, то система несовместна (i) (решений нет)

Если все i = 0, то решение существует и их бесконечно много. Система несовместна и называется неопределённой.

В случае неопределённой системы не все числа х1, х2, … , хn можно брать произвольными, так как даже если одно уравнение осталось в системе, а все остальные – следствие из него, то это уравнение связывает между собой переменные, а это и значит, что все их брать произвольными нельзя.

6. Необходимое и достаточное условие совместимости системы. Теорема Кронекера –

Капелле.

Система совместна тогда и только тогда, когда Rang А, составленный из коэффициентов при неизвестных, равен Rang Yрасширенной матрицы, т.е. матрицы, которая получена из матрицы A присоединением к ней столбца свободных членов.

Rang A = Rang Вектор столбец

(*)a1x1 + a2x2 +…+ anxn =b

1)Необходимость: Дано: совместная система, доказать: Rang A = Rang

Доказательство: Так как система совместна, то есть, имеет решение, то существует такой набор чисел x1=c1 , x2=c2 , xn=cn , при подставлении которых в систему (*) получится верное равенство. Следовательно, b есть линейная комбинация остальных столбцов.

1x1 + 2x2 +…+ nxn =

-> линейная комбинация столбцов . Если в матрице один столбец является линейной комбинацией остальных, то при добавлении к матрице А этого столбца, её Rang не меняется, т.е. Rang

A= Rang

2)Достаточность:

Дано: Rang A = Rang Доказать: система (*) совместна.

Доказательство: Матрицы A и отличаются только и т.к. их ранги равны, то дабавление к А

не меняет её ранга. Значит, этот столбец – линейная комбинация остальных столбцов. Т.е.

существует такие числа c1, c2, c3,…,cn, что 1c1+ 2c2+…+ ncn= . Но это и есть система (*) -> (*) удовлетворилась при x1=c1, x2=c2, xn=cn ч.т.д.

Т.е. с1,с2,сn – решения системы.

столбец с номером . Находим в нем ненулевой элемент и строку с этим элементом меняем местами с первой строкой. Чтобы не нагромождать дополнительных обозначений, будем считать, что такая смена

вывод, что система несовместна. Действительно, восстанавливая систему уравнений по расширенной матрице, получим, что -ое уравнение будет иметь вид

где По отношению к матрице выполняем описанный шаг алгоритма. Получаем матрицу

записать в виде

и к матрице снова применим описанный

выше шаг алгоритма.

Процесс останавливается, если после выполнения очередного шага новая уменьшенная матрица состоит из одних нулей или если исчерпаны все строки. Заметим, что заключение о несовместности системы могло остановить процесс и ранее. Если бы мы не уменьшали матрицу, то в итоге пришли бы к матрице вида

Далее выполняется так называемый обратный ход метода Гаусса. По матрице составляем систему уравнений. В левой части оставляем неизвестные с номерами, соответствующими первым ненулевым

элементам в каждой строке, то есть . Заметим, что . Остальные неизвестные переносим в правую часть. Считая неизвестные в правой части некоторыми фиксированными величинами, несложно выразить через них неизвестные левой части. Теперь, придавая неизвестным в правой части произвольные значения и вычисляя значения переменных левой части, мы будем

те неизвестные, которые явно не выписаны в правой части из-за нулевых коэффициентов, и тогда столбец неизвестных можно записать в виде столбца, где каждый элемент будет линейной

комбинацией произвольных величин (в частности, просто произвольной величиной

). Эта запись и будет общим решением системы. Если система была однородной, то получим общее решение однородной системы. Коэффициенты при , взятые в каждом элементе столбца общего

решения, составят первое решение из фундаментальной системы решений, коэффициенты при -- второе решение и т.д. Фундаментальную систему решений однородной системы можно получить и другим способом. Для этого одному переменному, перенесенному в правую часть, нужно присвоить значение 1, а остальным -- нули. Вычислив значения переменных в левой части, получим одно решение из фундаментальной системы. Присвоив другому переменному в правой части значение 1, а остальным -- нули, получим второе решение из фундаментальной системы и т.д. Замечание 15.4 У читателя может возникнуть вопрос: "Зачем рассматривать случай, когда некоторые столбцы матрицы нулевые? Ведь в этом случае соответствующие им переменные в системе уравнений в явном виде отсутствуют." Но дело том, что в некоторых задачах, например, при нахождении собственных чисел матрицы, такие системы возникают, и игнорировать отсутствующие переменные нельзя, так как при этом происходит потеря важных для задачи.