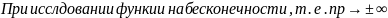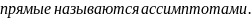18. Непрерывность функции в точке и на промежутке. Понятие о точках разрыва функции.

Функция 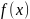называется не прерывной в точке 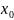, если предел функции и ее значение в этой точке равны.

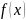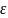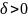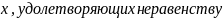
Функция называется не прерывной в точке _, если для любого >0 существует такое, что для всех 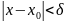выполняется неравенство

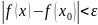
Функция называется не прерывной в точке , если ее приращение в этой точке является бесконечно малой функцией при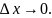

Функция называется не прерывной на отрезке если она не прерывна в каждой точке этого отрезка.

Точка называется точкой разрыва , если функция в точке не является непрерывной. Разрывы функции классифицируются следующим образом. Разрыв называется разрывом первого рода функции 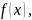если в этой точке функция имеет конечные, но не равные друг другу левые и правые пределы. Или, если в этой точке разрыв меняет одно конечное значение на другое, то это разрыв первого рода. В других случаях – второго.

19. Определение производной функции. Дифференциал. Правила дифференцирования. Дифференциалы высших порядков.

Производной функции y=f(x) в точке x₀ называется предел отношения приращения функции в этой точке к приращению аргумента (дельта x), при дельта x стремящемся к 0),

Функция имеет производную в точке тогда и только тогда, когда в этой точке существуют и равны между собой производные функции справа и слева.

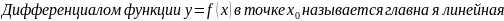
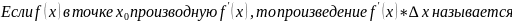
20. Признаки постоянства и, возрастания и убывания функции. Экстремум функции. Исследование функции на экстремум.

Признак монотонности функции: если функция дифференцируема на интервале (a;b), то функция возрастает (убывает) на этом интервале.

Внутренние точки области определения функции, в которой производная равна 0 или нее существует, называется критическими точками этой функции. Если производная меняет свой знак с + на - , то 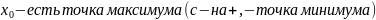. Точка максимума и минимума называются экстремумами или точками экстремума.

Необходимые условия существования экстремума:

Если функция в точке

.

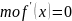Достаточное условие экстремума:

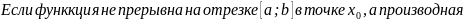
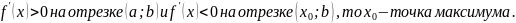
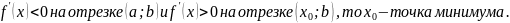
21. Основные теоремы дифференциального исчисления: Ферма, Рояля, Коши, Лагранжа

Теорема Ферма:

Если в точке функция достигает наибольшего или наименьшего значения на интервале и дифференцируема в , то .

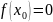Теорема Рояля:

Если функция фх не прерывна на отрезке (а,б) дифференцируема в каждой точке ч(а,б) и на концах отрезка принимает равные значения фа=фб то найдется точка с(а,б) (которую называют средней или промежуточной), такая что ф(с)=0

Теорема Лагранжи:

Пусть функция не прерывна на отрезке и имеет конечную производную во всех точках интервала (a;b), тогда найдется точка 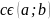в которой

Теорема Коши:

;

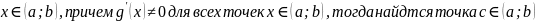
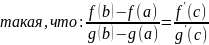22. Направление выпуклости и точки перегиба графика функции.

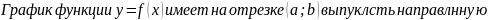
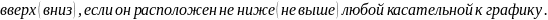
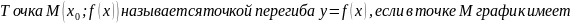
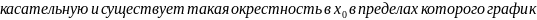
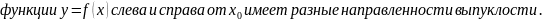
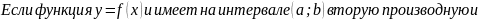
23. Понятие о пределе функции в точке. Поведение функции на бесконечности. Асимптоты.

Число A называется пределом f(x) в точке x=x₀, если для любой сходящейся к x₀ последовательность аргумента, отличных от x₀, существует последовательность значений функции сходящейся к A.