Экзаменационные вопросы по дисциплине «Элементы высшей математики»
Матрицы. Действия над ними. Свойства, миноры и алгебраические дополнения. Обратная матрица
Определители второго и третьего порядков. Свойства определителей, определитель n- го порядка.
Однородные и неоднородные системы линейных уравнений. Определитель системе n линейных уравнений с n переменными
Системы линейных уравнений, способы их решений (способ сложения, подстановки, графический).
Системы линейных уравнений. Решение систем линейных уравнений методами Крамера, Гаусса, способом матричного исчисления.
Общее уравнение прямой. Уравнение прямой с угловым коэффициентом. Уравнение прямой в отрезках.
Каноническое уравнение прямой. Параметрические уравнения прямой.
(на плоскости и в пространстве)
Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых.
Окружность. Уравнение окружности
Эллипс. Определение эллипса и вывод его канонического уравнения. Исследование формы эллипса.
Гипербола. Определение гиперболы и вывод её канонического уравнения. Исследование форм гиперболы.
Парабола. Определение параболы и её уравнения. Исследование формы параболы.
Геометрическая интерпретация комплексных чисел. Действительная и мнимая часть, модуль и аргумент комплексного числа.
Алгебраическая и тригонометрическая формы записи комплексных чисел.
Арифметические действия над комплексными числами в различных формах записи. Комплексно-сопряженные числа.
Предел числовой последовательности. Сходящиеся и расходящиеся последовательности. Теоремы о пределах последовательностей.
Предел функции в точке. Теоремы о пределах функции в точке.
Непрерывность функции в точке и на промежутке. Понятие о точках разрыва функции.
Определение производной функции. Дифференциал. Правила дифференцирования. Дифференциалы высших порядков.
Признаки постоянства и, возрастания и убывания функции. Экстремум функции. Исследование функции на экстремум.
Основные теоремы дифференциального исчисления: Ферма, Рояля, Коши, Лагранжа
Направление выпуклости и точки перегиба графика функции.
Понятие о пределе функции в точке. Поведение функции на бесконечности. Асимптоты.
Матрицы. Действия над ними. Свойства, миноры и алгебраические дополнения. Обратная матрица.
Матрица – математический объект, записываемый в виде прямоугольной таблицы элементов, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся ее элементы.
Определители второго и третьего порядков. Свойства определителей, определитель n- го порядка.
Определителем второго порядка соответствующем данной матрице называется число, которое обозначается символом \\ и определяется равенством:
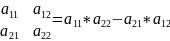
Определитель второго порядка равен произведению элементов, стоящих на главной диагонали, минус произведение элементов на побочной диагонали.
Определителем третьего порядка называется число, которое обозначается \\ и определяется равенством:
Методом треугольника:
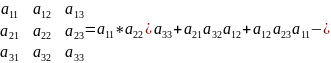
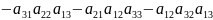
Методом дописывания строк:
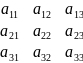
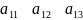
Методом разложения по элементам первой строки:
Определитель не изменится, если в нем строки заменить на столбцы, а столбцы на строки.
Строки и столбцы равноправны.
Если в определителе поменять местами какие-либо строки, то определитель поменяет только знак.
Если все элементы какой-либо строки имеют общий множитель, то его можно вынести за знак определителя.
Если у определителя все элементы какой-либо строки заданы как суммы двух слагаемых, то определитель равен сумме двух определителей, в одном из которых сумма заменена их первыми слагаемыми, а во втором вторыми.
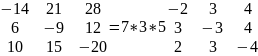
Однородные и неоднородные системы линейных уравнений. Определитель системы n линейных уравнений с n переменными
Если все свободные члены системы линейных уравнений равны 0, то система называется однородной, в противном случае неоднородной.
Любая однородная система линейных уравнений совместима. Любое частное решение однородной системы это упорядоченный набор чисел.
Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается дельтой (треугольником).
Если определитель системы отличен от нуля, то система линейных уравнений имеет одно решение, причем неизвестное равно отношению определителей.
Системы линейных уравнений, способы их решений (способ сложения, подстановки, графический).
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающих уравнении системы в верное равенство.
Системы линейных уравнений. Решение систем линейных уравнений методами Крамера, Гаусса, способом матричного исчисления.
Методом Крамера: (метод треугольника и т. д.)
Методом Гаусса:
Выберем разрешающую строку и в ней же разрешающий элемент.
Каждый элемент разрешающей строки разделим на разрешающий элемент.
Элементы разрешающего столбца заменим нулями во всех строках, кроме разрешающей.
Элементы столбцов, которые были разрешающими на предыдущих шагах исключения, переписываем без изменения.
Остальные элементы пересчитываем по правилу прямоугольника.
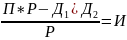
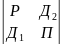
П – пересчитываемый
Р – разрешаемый
Д – диагональные
И - искомое
Общее уравнение прямой. Уравнение прямой с угловым коэффициентом. Уравнение прямой в отрезках.
Общее уравнение прямой:
В прямоугольной системе координат любая прямая задается уравнением первой степени и обратно, уравнение при произвольных коэффициентах A,B,C определяют некоторую прямую в прямоугольной системе координат.
Уравнение прямой с угловым коэффициентом:
Уравнение прямой в отрезках:
