VTA_pechatnye_lektsii_3_semestr

Добавил:

Hist Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

Векторный и тензорный анализ

Файл:

µD = ∫xdy = ∫a cos3 t 3 b sin 2 t cos t dt = 3ab ∫cos4 t

sin 2 t dt =

ab ∫cos2 t sin 2 2t dt =

.pdf

Скачиваний:

Добавлен:

10.05.2014

Размер:

1.75 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 115 6 7 8 9 10 11 > Следующая >>>

Введем обозначения ∂D1 =γ1+γ2 , ∂D2 =γ3+γ4= , тогда ∂D =γ1+γ4 . При этом ∫	+ ∫ =0. Тогда
γ 2	γ 3

	∂Q −	∂P
			dxdy =
∫∫D ∂x		∂y

D ∫∫+ D

∂Q −

∂P

∂Q −

∂P

∫∫D

∂Q −

∂P

dxdy =

∂x

∂y

∫∫D ∂x

∂y

∂x

∂y

∫Pdx + Qdy +

γ1 +γ 2

∫Pdx + Qdy = ∫Pdx + Qdy + ∫Pdx + Qdy + ∫Pdx + Qdy + ∫Pdx + Qdy = ∫Pdx + Qdy + ∫Pdx + Qdy

γ 3 +γ 4	γ 1	γ 2					γ 3	γ 4	γ 1	γ 4
= ∫Pdx + Qdy .

Пример 1. (4307) Вычислить ∫			xdy − ydx				. Контур C оринтирован положительно. Рассмотреть два

			x	2	+ y	2
	C		x		+ y
	C

случая: контур не содержит начало координат, контур содержит начало координат.

Обозначим через D область, ограниченную контуром C. Вычислим частные производные

∂Q =			∂						x							x	2	+ y			2		− 2x					2			y			2		− x			2
																	2				2							2						2					2
														=															=														,
								2				2		=					2					2		2			=				2					2			2		,
∂x								2	+ y			2					( x		2	+ y				2	)	2					( x		2		+ y			2		)	2
∂x		∂x x							+ y								( x			+ y					)						( x				+ y					)
∂P =	∂			−					y				= − x + y − 2 y																		=				y − x									,
																		2					2							2						2					2
																		2					2							2						2					2

						x	2		+ y		2							( x		2		+ y				2	)	2				( x				2	+ y				2	)		2
∂y ∂y						x			+ y									( x				+ y					)					( x					+ y					)
		∫				2				2								∂Q −					∂P
		∫				2				2					∫∫
Таким образом, в первом случае				xdy				− ydx						=													dxdy =0.
Таким образом, в первом случае														=													dxdy =0.
		C			x + y										D			∂x					∂y

Во втором случае формула Грина не может быть использована, так как поле (P,Q) имеет особенность в начале координат, которая попадает в область интегрирования. Выберем круг с центром в начале координат и достаточно малого радиуса r так, чтобы он содержался в области D. Границу этого круга, ориентированную положительно, обозначим Cr . Произведем два разреза кусочно-гладкими кривыми, соединяющие какие либо две точки границы контура C с какими либо точками окружности Cr . На рисунки в качестве разрезов выбраны отрезки прямой и показаны обозначения для некоторых кривых, образовавшихся в результате этих разрезов. Отметим, что

C=C1+C8 , Cr− =C3+C6 , C2= C7− , C4= C5− .

Внутри контуров C1+ C2+ C3+ C4 и C5+ C6+ C7+ C8 особенностей нет и, как было доказано, с Контур=C1+ C2+ C3+ C4+ C5+ C6+ C7+ C8 не содержит внутри себя ни каких особенностей векторного поля (P,Q) и, поэтому к нему применима формула Грина

∫

= ∫ + ∫ + ∫ + ∫ + ∫ + ∫ + ∫ + ∫ = ∫ + ∫ + ∫ = ∫ − ∫ .

C1 +C 2 +C3 +C 4

C5 +C6 +C7 +C8 C1

C4 C5 C6

C7 C8 C

C3 C6 C C r

xdy − ydx

2π r cos t(r cos t) − r sin t(−r sin t)

Таким образом. ∫

= ∫

dt = 2π .

+ y

Пример 2. (4303) Вычислить

∫(sin yex − my)dx + (cos yex − m)dy , где AmB – верхняя

AmB

полуокружность x2+y2=ax , начало - A(a,0), конец – B(0,0).

∂Q =

∂

(cos yex

− m)= cos yex ,

∂P =

∂

(sin yex

− my)= cos yex − m .

∂Q −

∂P = m .

∂x

∂y

∂x

∂y

∫

Pdx + Qdy +

∫

Pdx + Qdy =

∫

Pdx + Qdy = =

∂Q − ∂P

dxdy = m

∫∫

dxdy = mµD = m πa

∫∫

∂y

AmB

AmB + BA

D ∂x

∫Pdx + Qdy = m πa2

− ∫Pdx + Qdy = m πa2

+ ∫Pdx + Qdy .

AmB

				x = t
AB- имеет параметризацию				y = 0 t [0, a] .
Тогда
∫Pdx + Qdy = m πa		2	a		2
∫Pdx + Qdy = m πa			+ ∫(0)dt = m πa		.
AmB	8		0	8
AmB			0
Пример 3. (4304) Вычислить				∫( f ( y)ex − my)dx + ( f '( y)ex − m)dy , где функция f(y) – непрерывно
				AmB

дифферинцированная на проекции кривой AmB функция (проекция на ось Oy), AmB – кривая, соединяющая точки A, B, ограничивающая вместе в отрезком AB область D.

∂Q =

∂

(f '( y)ex − m)= f '( y)ex ,

∂P =

∂

(f ( y)ex − my)= f '( y)ex − m .

∂Q −

∂P = m .

∂x

∂y

∂x

∂y

Pdx + Qdy +

Pdx + Qdy =

Pdx + Qdy = =

∂Q −

= m

dxdy = mµD .

∫

∂P dxdy

∫∫

∂x

AmB

AmB + BA

∂y

∫Pdx + Qdy =mµD − ∫Pdx + Qdy = mµD + ∫Pdx + Qdy .

AmB

x = x0

x t

AB- имеет параметризацию

t [0,1] , A=(x0,y0),B=(x1,y1), x=x1 - x0 , y=y1 - y0 .

y = y0

y t

Тогда

∫Pdx + Qdy = ∫1		((f ( y0	+	y t)ex0 +	x t − m( y0	+	y t))	x + (f '( y0	+	y t)ex0 +	x t
AB	0
∫Pdx + Qdy = ∫1		((f ( y0	+	y t)ex0 +	x t − m( y0	+	y t))	x + (f '( y0	+	y t)ex0 +	x t
AB	0

−m) y)dt =

∫((f ( y0 + y t)ex0 + x t )	x)dt + ∫(− m( y0	+ y t) x)dt + ∫(f '( y0 + y t)ex	0 + x t	y)dt −
1	1	1
0	0	0

(f ( y

+ x t

)d ( x

(f '( y

+ x t

)d ( y

∫

m ydt =

∫

xt) − m

∫

+ y t) −

y t)e 0

x y

y t)e 0

u − x

u − y

∫

m y =

f ( y

+ y

)eu du − m x y

df (u) -

u − x

m y =

∫

f ( y

+ y

)eu du − m

x y

− y

x +

u − y

u = y1

u − y

f (u)

− ∫

f (u)du = ∫

u = y

x +

u − y

u = y1

x +

m x y +

−

f (u)

−

∫

u = y

f (v)			x	e	x0 +
			x

			y
u − y		0
x		0			x
x	y
	y

					y

x (v − y )
y	0	dv −




f (u)du =

− m xy + m x y − m y + ex1		f ( y ) − ex0 f ( y		) .
0	2	1	0
	2
∫Pdx + Qdy = mµD+ − m xy0		+ m	x y − m y + ex1 f ( y1 ) − ex0 f ( y0 ) .
AmB			2
AmB

2.Использование формулы Грина для вычисления площадей.

Если в качестве функций P, Q взять функции, для которых ∂Q − ∂P ≡ 1 , то получится формула для

∂x ∂y

вычисления площади области, ограниченной кривой γ .

D =

∫∫

dxdy =

∂Q −

∂P

∫

Pdx + Qdy .

dxdy =

∫∫

∂x

∂y

Можно предложить три варианта таких функций

Q=x, P=0 и тогда D = ∫xdy .

Q=0, P=-y и тогда D = −∫ ydx .

, P= −

и тогда D = −

∫ ydx − xdy .

Пример 1. Вычислить площадь астроиды

x = a cos	3	t		t [0,2π ]

y = b sin3 t

2π

3 ab ∫(1 + cos 2t) (1- cos 4t) dt = 3 π ab.

16 8

Пример 2. Вычислить площадь лемнискаты (x2+y2)2=a2(x2-y2).

В полярных координатах r = a

cos 2ϕ

x = a

cos 2ϕ cosϕ

ϕ [−

Параметризация правой ветви

= a

] .

cos 2ϕ sin ϕ

4 4

µD =

2∫xdy =2 ∫

(−2 sin 2ϕ) sin

ϕ +

cos 2ϕ cosϕ

cos 2ϕ

cos 2ϕ cosϕ

dϕ =

−

1 + cos 2ϕ

1 1 − cos 4ϕ

− 2a

∫cosϕ sin 2ϕ sin ϕ dϕ + 2a

∫cos 2ϕ cos

ϕ dϕ = 2a

∫

cos 2ϕ

−

dϕ =

−

1 + cos 4ϕ

cos 4ϕ

∫

cos 2ϕ

−

dϕ

= a π .

−

3. Условия независимости интеграла второго рода от пути интегрирования.

Определение. Область называется односвязной, если ее граница представляет собой связное множество. Область называется n-связной, если ее граница распадается на n- связных множеств.

Замечание. Формула Грина верна и для многосвязных областей.

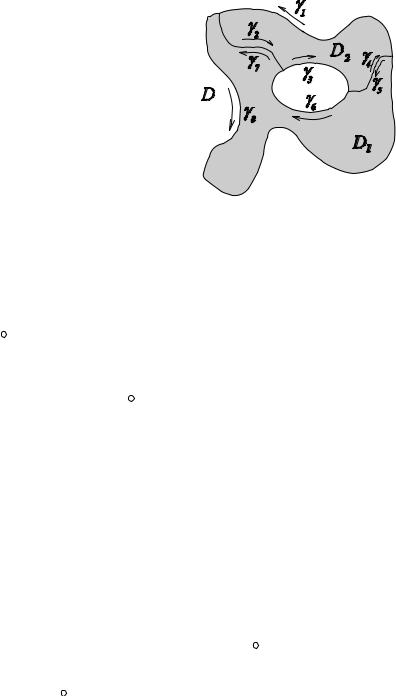
Например, для области, показанной на рисунке произведены разрезы, соедеиняющие обе связные компоненты границы между собой.

Можно выписать цепочку равенств

∂Q −

∂P

∂Q − ∂P

∂Q −

∂P

∂Q −

Pdx + Qdy +

dxdy =

∫∫

dxdy =

∂P =

∫

∫∫

∂x

∂y

∫∫

∂x

∫∫

∂x

∂y

D + D

∂y

∂y γ

+γ

∫Pdx + Qdy = ∫

+ ∫

= ∫

+ ∫

+ ∫ =

∫

∫ =

γ 5 +γ 6 +γ 7 +γ 8

γ 1

γ 2

γ 3

γ 4

γ 5

γ 6

γ 7

γ 8

γ 1

γ 3

γ 6

γ 8

γ 1 +γ 8

γ 3 +γ 6

∫Pdx + Qdy .

∂D

Замкнутая кривая называется контуром. Криволинейный интеграл второго рода в этом случае иногда обозначается ∫ .

До конца этого пункта будем считать, что область D - открытое и односвязное множество, а функции

P(x,y), Q(x,y) непрерывны в замыкании D вместе со своими производными		∂P		∂Q
		∂y	,	∂x .
Лемма. Для того, чтобы интеграл
∫Pdx + Qdy	(4)
AB

( A, B – любые точки из D ) не зависел от пути интегрирования ( а только от начальной и конечной точек A, B ) необходимо и достаточно, чтобы по любой замкнутой кривой (по любому контуру) лежащей в D интеграл (4) был равен нулю

∫Pdx + Qdy =0.

Интеграл ∫Pdx + Qdy называется циркуляцией векторного поля V=(P,Q).

Доказательство (необходимость). Пусть (4) не зависит от пути интегрирования. Рассмотрим произвольный контур C, лежащий в области D и выберем две произвольные точки A, B на этом контуре. Тогда кривую C можно представить, как объединение двух кривых 2 (из A в B, как на рисунке ) и 1 (тоже из A в B, но по другой ветви ), C= 1− + 2 .

По условию			∫ = ∫		, кроме того ∫	= − ∫	, поэтому ∫	= ∫	+ ∫	= ∫	- ∫ =0. Для доказательства
					−		C		−
			2	1	1	1		2	1	2	1
достаточности рассмотрим две точки A, B в области D и два пути AB= 2 , AB= 1 соединяющие эти
две точки. Рассмотрим контур C= 1−						+ 2 . По условию ∫ =0 , откуда, с учетом соотношения
								C
∫	= ∫	+ ∫	= ∫	- ∫	, следует требуемое равенство ∫			= ∫	. В этом доказательстве
C		−
	2	1	2	1			2	1

предполагается, что кривые 2 , 1 не пересекаются. Самостоятельно доказать это утверждение для случая, показанного на рисунке ниже

Теорема 1. Для того, чтобы криволинейный интеграл (4) не зависел от пути интегрирования в D, необходимо и достаточно чтобы

∂Q ≡	∂P в области D.	(5)
∂x	∂y

Достаточность. Если (5) выполнено, то формуле Грина для любого контура C будет

∫	Pdx + Qdy =		∂Q −	∂P
					dxdy =0,
		∫∫	∂x
C				∂y

откуда по лемме следует требуемое утверждение.

Необходимость. По лемме для любого контура ∫				= 0. Тогда по формуле Грина для области ,
			C
ограниченной этим контуром	∫∫	∂x ∂y			∫∫	∂x ∂y
	∫∫	∂x ∂y			∫∫	∂x ∂y
		∂Q − ∂P	dxdy =0. По теореме о среднем 0=			∂Q − ∂P	dxdy =

∂P

∫∫

∂Q −

∂P

или ∂Q −

=0. Переходя к пределу, стягивая контур к точке,

∂x

∂y

M θ

∂x

∂y

M θ

получим, что в этой точке

∂Q −

∂P = 0 .

∂x

∂y

Теорема 2. Для того, чтобы криволинейный интеграл (4) не зависел от пути интегрирования в D, необходимо и достаточно чтобы подинтегральное выражение Pdx+Qdy являлось полным дифференциалом некоторой непрерывно дифференцируемой функции u(x,y) в области D

du = Pdx+Qdy		(6)
Достаточность. Пусть (6) выполнено, тогда	∂u = P ,	∂u = Q ,	∂Q =	∂P и можно сослаться на
	∂x	∂y	∂x	∂y

теорему 1.

Необходимость. Пусть интеграл не зависит от пути интегрирования. Фиксируем некоторую точку A0 в области D и определим функцию

u(A) = u(x,y)= ∫Pdx + Qdy .

A0 A

В этом случае

	u( x + x, y) − u( x, y)		1				1	x + x
		=		∫Pdx + Qdy =				∫P(t, y)dt = P(ξ , y) , ξ [x,x+		x] (ξ [x+ x,x]). Таким
	x		x				x
				AB				x

образом, существует производная					∂u	=P.	Аналогично, проверяется, что		∂u	=Q. При сделанных
					∂x				∂y

предположениях функция u оказывается непрерывно - дифференцируемой и du = Pdx+Qdy.

Замечание 1. Условие односвязности области D в сформулированных теоремах существенно.

Ранее был рассмотрен пример с интегралом ∫

xdy − ydx

, где

∂Q

∂P

y2 − x2

. В случае, когда

+ y

∂x

∂y

( x

)

область содержит начало координат, полученная область является двусвязной, в частности, интегралы по контурам, содержащим начало координат не равны нулю.

Замечание 2. При доказательстве теоремы 2 была построена функция u(x,y)= ∫Pdx + Qdy . Эта

A0 A

функция определяется с точностью до аддитивной постоянной и называется потенциалом (скалярным) векторного поля (P,Q).

Пример. Решить дифференциальное уравнение (f ( y)ex − my)dx + (f '(

Для поля V = (P, Q) = (f ( y)ex − my, f '( y)ex − mx) будет выполнено

y)ex − mx)dy = 0 .

∂P = f '( y)ex − m =	∂Q .
∂y	∂x

В этом случае для функции u(x,y)= ∫Pdx + Qdy выполняется равенство du = Pdx+Qdy и,

A0 A

следовательно, u(x,y)=Const есть решение исходного дифференциального уравнения. Найдем функцию u. Пусть M =(x, y) текущая точка области M0=(0,0). В качестве кривой, соединяющей точки M0 и M , выберем отрезок

γ: x t t [0,1] , y t

u( x, y) = u(M ) = ∫Pdx + Qdy = ∫((f ( yt)ext − myt )x + (f '( yt)ext − mxt )y)dt = x∫ f ( yt)ext dt +
		1	1
γ		0	0
1	1	1	1
y∫ f '( yt)ext dt − mxy = x∫ f ( yt)ext dt + ∫ext df ( yt) − mxy = x∫ f ( yt)ext dt +
0	0	0	0
	1
[ f ( y)ex − f (0)] − x∫ f ( yt)ext dt − mxy = f ( y)ex − f (0) − mxy .
	0
		Глава 4.	Поверхностные интегралы
		§1. Поверхностные интегралы 1-го рода

1.Площадь поверхности, заданной уравнением z=f(x,y)

Будем предполагать, что функция f(x,y) определена и непрерывна вместе со своими частными

производными	∂f	,	∂f	в области D. Обозначим эти производные p=	∂f	, q=	∂f	. Уравнение
	∂x		∂y		∂x		∂y

касательной плоскости в точке (x,y,z) имеет вид Z – z = p (X – x) +q(Y – y) (здесь X, Y, Z – текущие

точки плоскости). Нормаль к этой плоскости N

=±(p, q, -1), n

. Направляющие косинусы

нормали равны

cos( n , i )

cos( n , j )

cos( n , k )

cos α

cos β

cos γ

+ p2 + q2

+ p2

+ q2

Возьмем какое-либо разбиение {Di} области D. Цилиндры с основаниями Di вырезают на поверхности z=f(x,y) области Si = {(x,y,z): (x,y) Di , z = f(x,y) }.

На Sk выберем промежуточную точку Mk(ξk ,ηk , ζk) , ζk = f(ξk ,ηk ). В этой точке построим касательную плоскость. Цилиндр с основание Dk вырезает на этой плоскости фигуру Tk с некоторой площадью µTk .

Известно, что

r	r
µDk = µTk \|cos( n , k )\|.
Таким образом

µTk =µDk

1 + p2 (ξ

,η

) + q2

(ξ

,η

) .

За площадь поверхности z=f(x,y) принимается число

µS= lim ∑µTk

= lim

∑ 1 + p2 (ξk ,ηk ) + q2 (ξk ,ηk )µDk = ∫∫

1 + p2

( x, y) + q2

( x, y)dxdy = ∫∫

dxdy .

λ →0

Докажем равенство µDk = µTk |cos( n , k )|. Рассмотрим цилиндр с основанием D, ограниченный сверху плоскостью. При необходимости систему координат можно повернуть вокруг оси Oz, так что можно считать, что уравнение верхней крышки цилиндра будет не содержать y: z = ax=x tg α .

<<< < Предыдущая 1 2 3 45 / 115 6 7 8 9 10 11 > Следующая >>>

Соседние файлы в папке ВТА экзамен 3 семестр

#
10.05.2014221.39 Кб43Pechatnye_shpory.docx
#
10.05.2014214.33 Кб36Pechatnye_shpory_po_VTA_1_potok_chitat.docx
#
10.05.2014221.39 Кб36Pechatnye_shpory_po_VTA_I_potok.docx
#
10.05.20141.75 Mб44VTA_pechatnye_lektsii_3_semestr.pdf
#
10.05.201418.74 Кб32Доп вопросы по матану.docx
#
10.05.2014381.71 Кб33Доп вопросы по матану.pdf
#
10.05.2014932.72 Кб55Печатные Шпоры, читать.pdf
#
10.05.201417.57 Кб35список вопросов ВТА (печатные).docx
#
10.05.201415.44 Кб36Список вопросов ВТА.docx