19.Случайные величины – дискретные и непрерывные. Определение и примеры.

ДСВ- такая величина, которая в результате опыта может принимать определенные значения с определенной вероятностью, образующие счетное множество (множество, элементы которого могут быть занумерованы).Пр.Х-кол-во студентов, опоздавших на 1ую пару(1,2,..),У-оценка, плученная студентом на экзамене(1,2,3,4,5).

НСВ-  такая величина, которая может принимать любые значения из некоторого конечного или бесконечного промежутка.Пр. Z-

дальность полёта снаряда (α;β).

20.Закон распределения дискретной случайной величины – определение. (вывод).

Соответствие м\у возможными значениями дсв и их вер-ми

Х	х1	х2	х3	…	хп
Р	р1	р2	р3	…	рп

Док-во: (Х=х₁)-событие, что случ вел х приняла значение х_n

… (Х=х _n); (Х=х₁)+ (Х=х₂)+…+ (Х=х _n)=U-достоверное событие несовм событий. Р(Х=х₁)+Р(Х=х₂)+…+Р (Х=х _n)=Р(U), Р₁+Р₂+…+Р_n=1 ,

∑_iР_i=1-ч т д.

21.Биномиальное, геометрическое (бесконечное и с ограничением) распределения, распределение Пуассона – определения.

Если производится независимых испытаний, в каждом из которых событие может появиться с одинаковой вероятностью в каждом из испытаний, то вероятность того, что событие не появится, равна . Примем число появлений события в каждом из испытаний за некоторую случайную величину 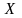. Чтобы найти закон распределения этой случайной величины, необходимо определить значения этой величины и их вероятности.

Вероятность каждого значения этой случайной величины можно найти по формуле Бернулли.

Эта формула аналитически выражает искомый закон распределения. Этот закон распределения называется биноминальныv

Геометри́ческое распределе́ние в теории вероятностей —распределение дискретной случайной величины равной количеству испытаний случайного эксперимента до наблюдения первого «успехаПусть   — бесконечная последовательностьнезависимых случайных величин с распределением Бернулли, то есть

Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга. Выберем фиксированное число   и определимдискретное распределение, задаваемое следующей функцией вероятности:

,

где  обозначает факториал числа  ,  — основание натурального логарифма.

Тот факт, что случайная величина   имеет распределение Пуассона с параметром  , записывается:  .

22. Математическое ожидание дискретной случайной величины, его вероятностный и механический смысл (вывод).

Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.Математическое ожидание M дискретной случайной величины - это среднее значение случайной величины, равное сумме произведений всех возможных значений случайной величины на их вероятности.