6.9. Согласованная нагрузка

Линия с распределенными параметрами, как правило, служит в качестве промежуточного звена между источником энергии (сигнала) и нагрузкой.

Обозначим сопротивление нагрузки Z₂ (Z₂=U₂/I₂) (рис.6.5).

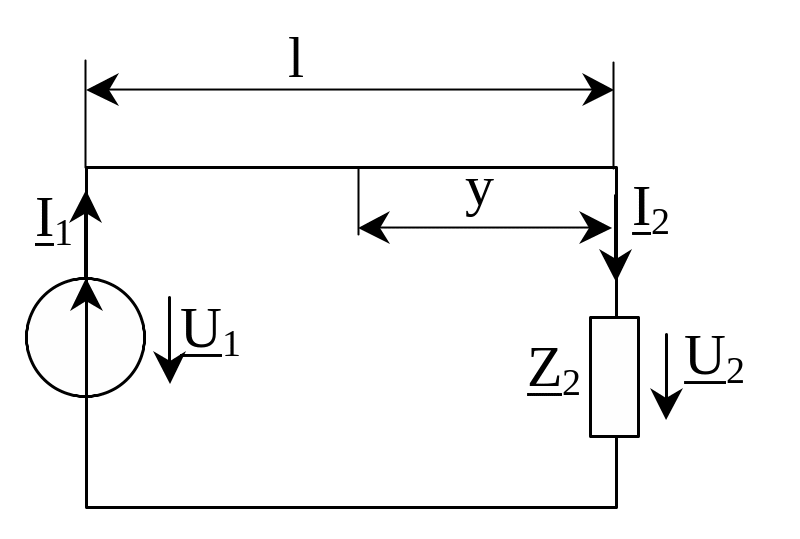
Рис. 6.5. Схема длинной линии, подключенной к источнику с напряжением U₁, и нагрузке Z₂

Если Z₂Z_В, то падающая волна частично пройдет в нагрузку, частично отразится от нее (возникает отраженная волна). При Z₂=Z_В - такую нагрузку называют согласованной, отраженная волна отсутствует. В этом можно убедиться с помощью формулы (6.28). Действительно, отраженная волна отсутствует, так как С₁=0. Чтобы получить формулы для определения напряжения и тока в любой точке, удаленной от конца линии на расстояние у, в формулы (6.29) и (6.30) вместо Z_B подставим Z₂, заменим I₂Z₂ на U₂ и U₂/Z₂ на I₂. Получим:

U=U₂(chy+shy)=U₂e^y,

I=I₂(chy+shy)=I₂e^y.

В начале линии при у=1

(6.39)

Из уравнения (6.39) ,

где Z_B и _В- соответственно модуль и аргумент волнового сопротивления.

Коэффициент полезного действия линии передачи равен отношению активной мощности в конце линии Р₂ к активной мощности в начале линии Р₁:

P₁=U₁I₁cos_B,

При согласованной нагрузке угол между U₂ и I₂ также равен _В, поэтому в соответствии с формулами (6.39)

.

Следовательно,

.

6.10. Входное сопротивление нагруженной линии

На рис.6.5 изображена схема, состоящая из источника напряжения U₁, линии с распределенными параметрами длиной l и нагрузки Z₂. Входное сопротивление Z_BX=U₁/I₁. При у =l получим

,

или

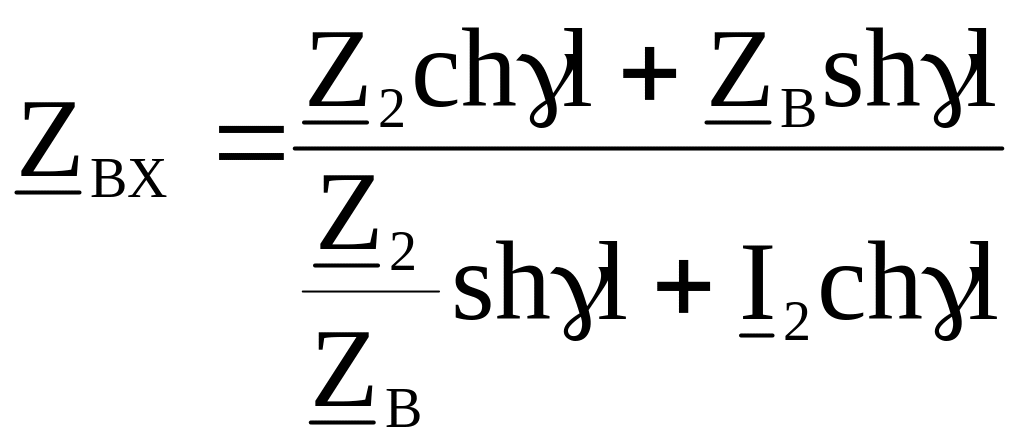. (6.40)

Если нагрузка согласована (т.е. Z_BX= Z₂)_, то из (6.40) следует, что входное сопротивление равно волновому: Z_BX=Z_B.

6.11. Определение напряжения и тока в линии без потерь

В линиях передачи электрической энергии при достаточно высокой частоте можно с большой точностью пренебречь сопротивлением R₀ и проводимостью утечки G₀ по сравнению соответственно величинами L₀ и С₀. Поэтому во многих случаях такие линии рассматривают как величины без потерь энергии, что является идеализацией реальной линии.

Для линии без потерь коэффициент распространения

,

т.е. коэффициент затухания =0, а коэффициент фазы = .

При этом волновое сопротивление Z_B= является чисто активным.

Для определения напряжения U и тока I в любой точке линии в (6.29) и (6.30) , учтем, что y=(+j)y=(0+j)y=jy и chjy =cosy, shjy=siny.

Поэтому для линии без потерь формулы (6.29) и (6.30) перепишем следующим образом:

U=U₂cosy+jI₂Z_Bsiny, (6.41)

. (6.42)

6.12. Входное сопротивление линии без потерь при холостом ходе и коротком замыкании

При холостом ходе I₂=0. Поэтому

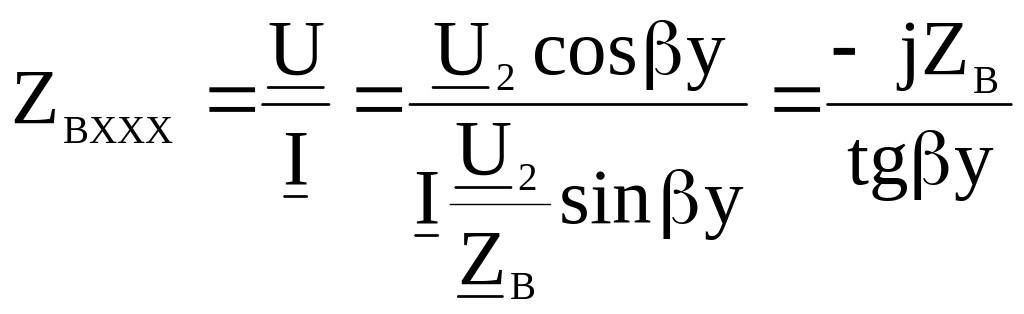. (6.43)

Исследуем характер изменения Z_BXXX при изменении расстояния у от конца линии до текущей точки на ней.

В интервале значений у от 0 до /2 tgy изменяется от 0 до , поэтому Z_BXXX имеет емкостный характер (множитель -j) и по модулю изменяется от  до 0. Расположение кривой выше оси абсцисс соответствует индуктивному характеру реактивного сопротивления, расположение кривой ниже оси - емкостному (рис.6.6,а).

Рис, 6.6. Характер изменения входного сопротивления линии без потерь в режиме ХХ и КЗ

В интервале значений у от /2 до  tgy отрицательный и изменяется от - до 0, поэтому Z_BXXX изменяется по модулю от 0 до  и имеет индуктивный характер (множитель +j) и т.д.

Таким образом, изменяя длину отрезка линии без потерь, можно имитировать емкостное и индуктивное сопротивление любой величины. Практически это свойство используют при высокой частоте в различных радиотехнических установках.

При коротком замыкании U₂=0

Z_BXКЗ=jZ_Btgy. (6.44)

Будем изменять длину отрезка линии у и исследуем характер входного сопротивления.

В интервале значений у от 0 до /2 tgy положителен и изменяется от О до ∞, следовательно, в этом интервале входное сопротивление имеет индуктивный характер и по модулю изменяется от 0 до ∞ (рис.6.6,б).

В интервале у от /2 до  входное сопротивление имеет емкостный характер и изменяется по модулю от ∞ до 0 (в точке у=/2 tgy скачком изменяется от + ∞ до - ∞)(рис.6.6,б).

Таким образом, изменяя длину отрезка короткозамкнутой на конце линии, также можно создавать различные по величине индуктивные и емкостные сопротивления. Отрезок короткозамкнутой на конце линии без потерь длиной в четверть длины волны теоретически имеет входное сопротивление, равное бесконечности. Это позволяет применять его при подвеске проводов в качестве изолятора.