3.2Ручной счет решения нелинейного уравнения

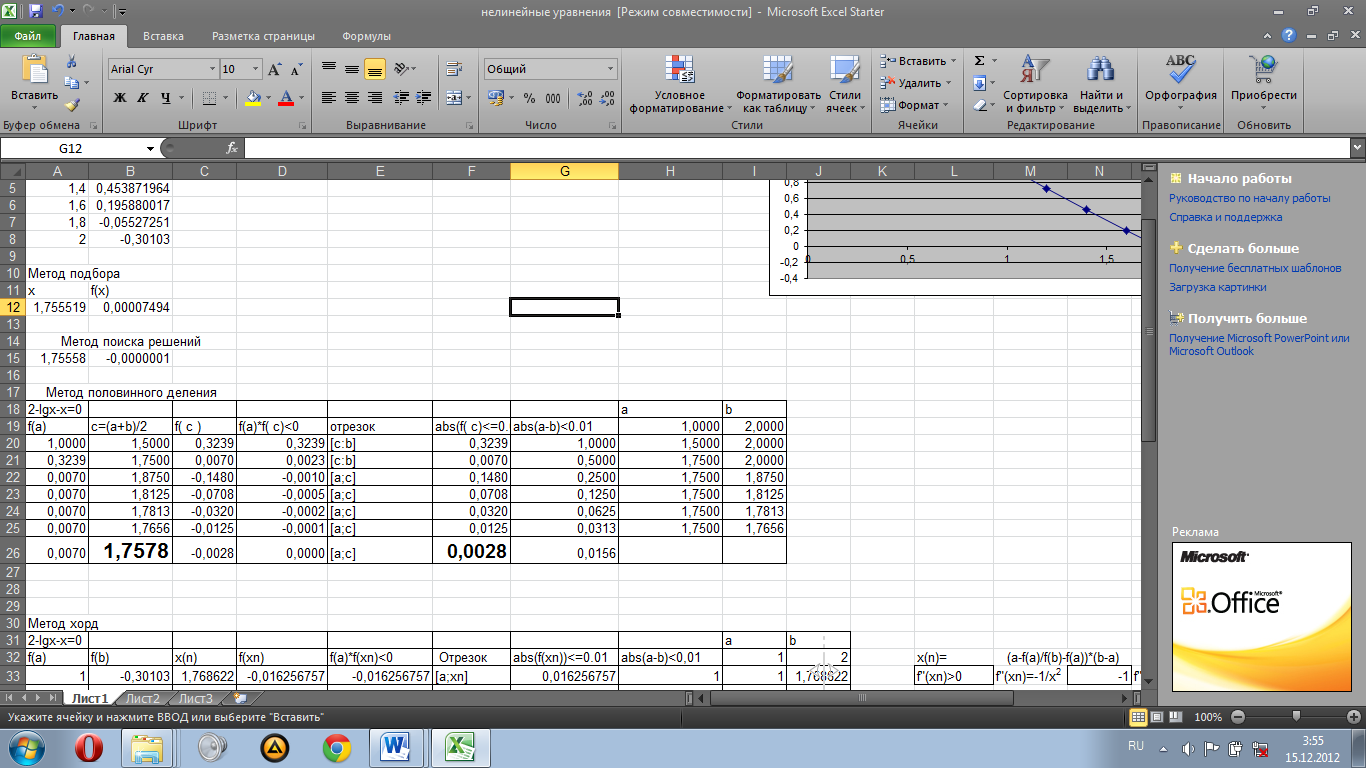
3.2.1Ручной счет методом половинного деления

Если а=1 и b=2; c₀=(a+b)/2= 1,5; f(a)*f(c)=0,324>0=>[c0;b];

c₀=1,5 и b=2; c₁=(c₀+b)/2=1,75; f(c₀)*f(c₁)=0,002>0=>[c₁;b];

c₁=1,75 и b=2; c₂=(c₁+b)/2=1,875; f(c₁)*f(c₂)=-0,001<0=>[ a;c1];

c₁=1,75 и c₂=1,875; c₃=(c₁+c₂)/2=1,813; f(c₁)*f(c₃)=0<0=>[ a;c₂];

c₁=1,75 и c₃=1,813; c₄=(c₁+c₃)/2=1,781; f(c₁)*f(c₄)=0>0=>[ a;c₃];

c₄=1,75 и c₃=1,781; c₅=(c₄+c₃)/2=1,766; f(c₄)*f(c₅)=0>0=>[ a;c₄];

c₄=1,75 и c₃=1,766; c₆=(c₅+c₃)/2=1,758; => c₆=1.758- является корнем нашего уравнения, т.к. |f(с₆)|= 0,003<0.01.

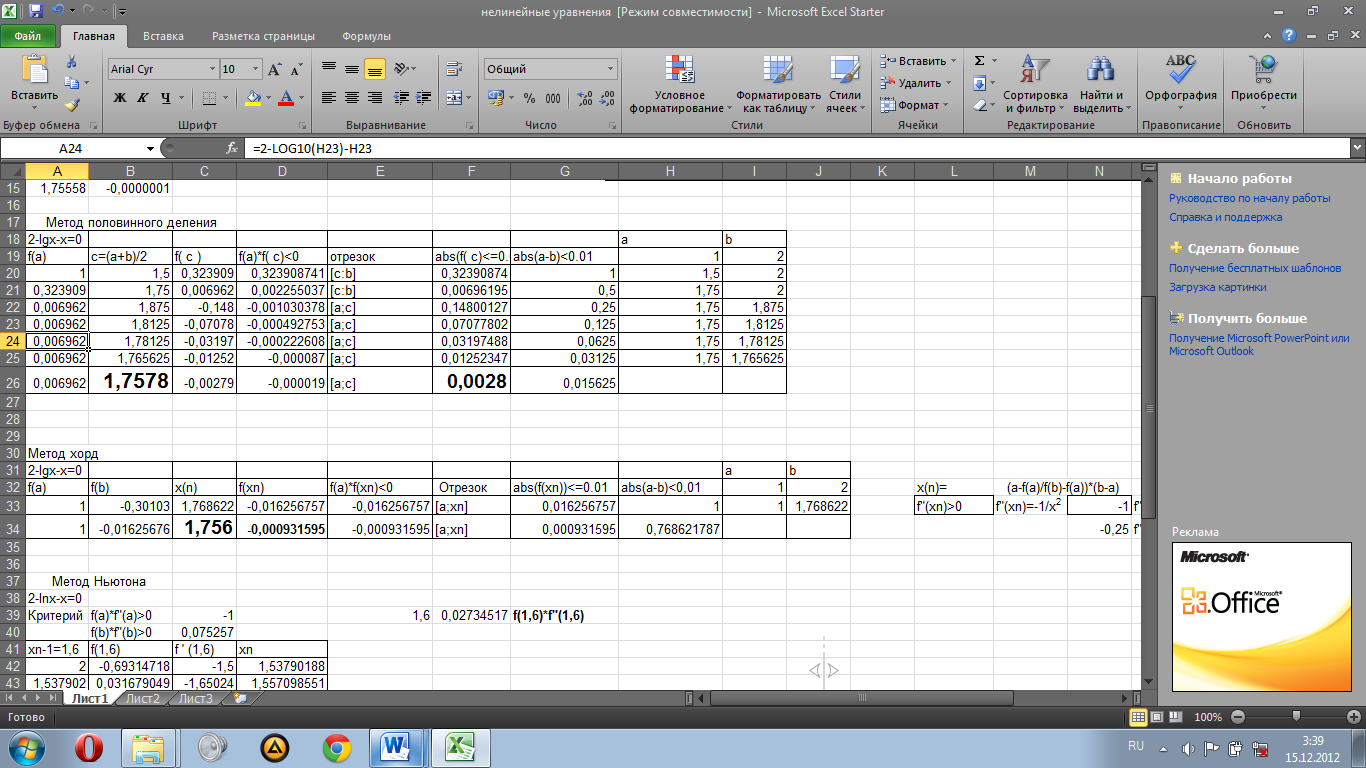
3.2.2Ручной счет по методу хорд

Для нахождения корня уравнения , принадлежащего отрезку , будем использовать формулу:

;

Если <= , то x корень уравнения. В противном же случаи выбираем ту из половин или на концах которой имеет разные знаки. В новом отрезке сновап применяем формулы хорды и также расчитываем пока не станет меньше либо равно .

Найдём f"(xn)=-1/x² ,f"(a)=-1, f"(b)=-0,25. Условие выполняется, т.к f”(a)*f”(b)>0.

3.3Графическое решение нелинейного уравнения в excel

4Построение графиков и поверхностей

4.1Построение графиков

x	y	z
-3	0	-1
-2,5	-1	0
-2	0	1
-1,5	-1	0
-1	0	-1
-0,5	-1	0
0	0	1
0,5	-1	0
1	0	-1
1,5	-1	0
2	0	1

Для y=SIN(3*ПИ()*A2)*SIN(ПИ()*A2)

Для z=COS(4*ПИ()*A2)^3*COS(ПИ()*A2)